Giá trị của tham số $m$ sao cho tiệm cận ngang của đồ thị hàm số $y=\dfrac{mx+5}{x+1}$ đi qua điểm $M(2;-4)$ là
| $4$ | |
| $-4$ | |
| $-2$ | |
| $2$ |
Cho hàm số $y=f(x)$ có $f'(x)$ liên tục trên $\mathbb{R}$ và đồ thị $f'(x)$ như hình bên.
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
| $(-\infty;0)$ | |
| $(-1;1)$ | |
| $(1;4)$ | |
| $(1;+\infty)$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
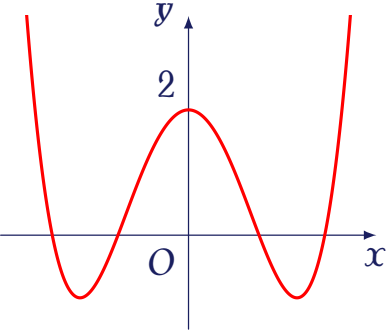
Số nghiệm của phương trình $f(x)-1=0$ là
| $2$ | |
| $1$ | |
| $4$ | |
| $3$ |
Cho hàm số $y=ax^3-3x^2+b$ ($a\neq0$) có bảng biến thiên như sau:
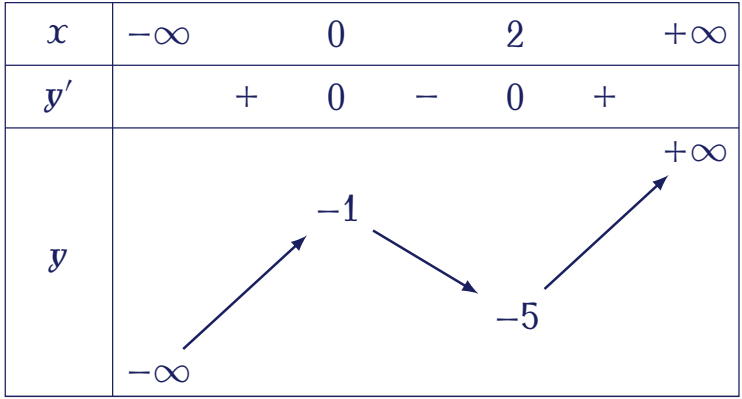
Mệnh đề nào dưới đây đúng?
| $a>0,\,b< 0$ | |
| $a< 0,\,b>0$ | |
| $a>0,\,b>0$ | |
| $a< 0,\,b< 0$ |
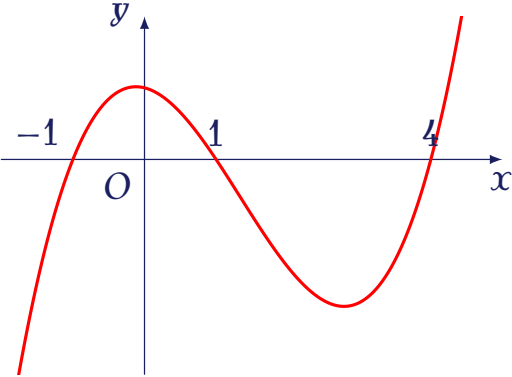
Cho hàm số $y=f(x)$ có đồ thị là đường cong trong hình bên.
Giá trị của tham số $m$ để phương trình $f(x)+1=m$ có ba nghiệm phân biệt là
| $0< m< 4$ | |
| $1< m< 5$ | |
| $-1< m< 4$ | |
| $0< m< 5$ |
Cho hàm số $y=f(x)$ có bảng biến thiên trên đoạn $[-1;3]$ như sau:
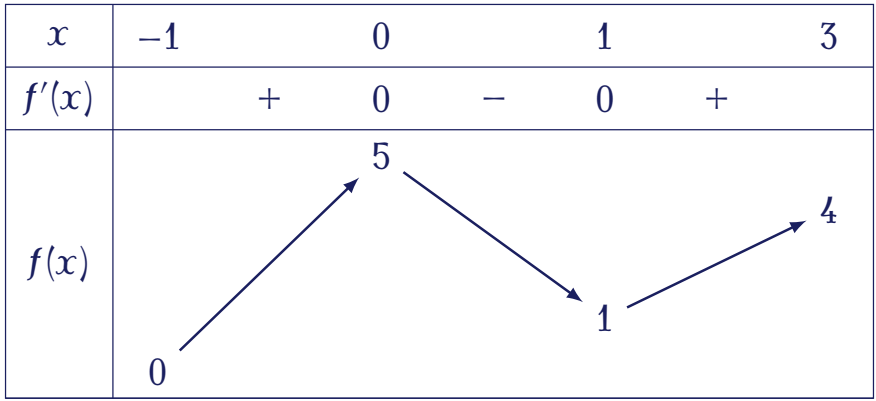
Giá trị lớn nhất của hàm số đã cho trên đoạn $[-1;3]$ bằng
| $1$ | |
| $4$ | |
| $0$ | |
| $5$ |
Cho hàm số $y=f(x)$ có bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số đã cho bằng
| $3$ | |
| $0$ | |
| $1$ | |
| $2$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
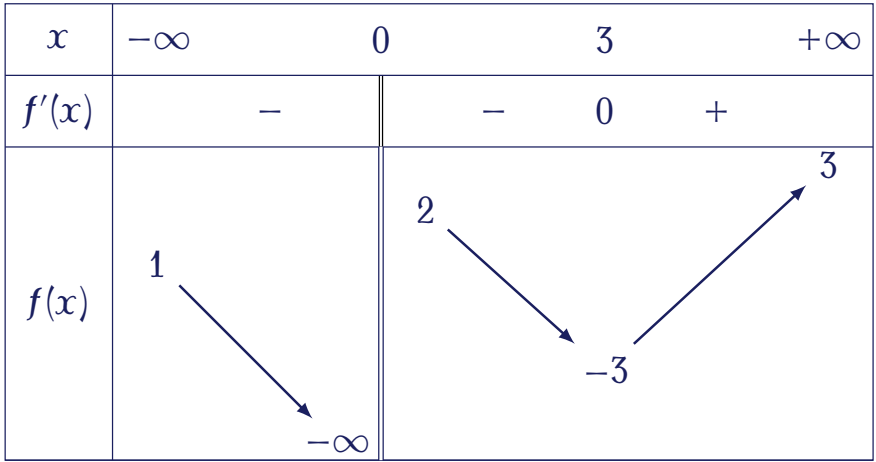
Tiệm cận đứng của đồ thị hàm số đã cho là
| $x=3$ | |
| $x=2$ | |
| $x=0$ | |
| $x=1$ |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên dưới.
Hàm số đã cho đồng biến trên khoảng nào sau đây?
| $(2;+\infty)$ | |
| $(-2;2)$ | |
| $(0;2)$ | |
| $(-\infty;2)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
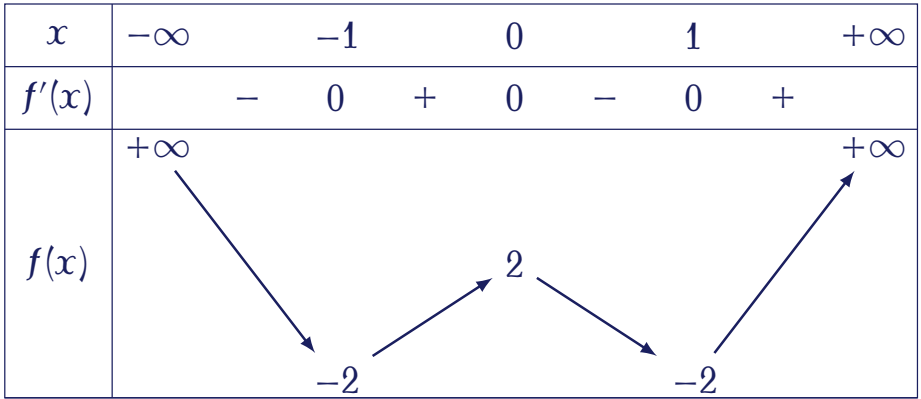
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(-\infty;1)$ | |
| $(0;1)$ | |
| $(-1;0)$ | |
| $(-2;+\infty)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
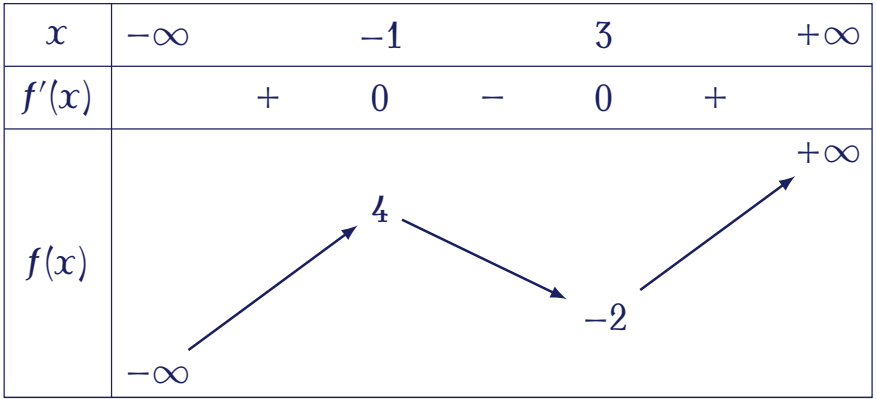
Giá trị cực đại của hàm số đã cho bằng
| $-2$ | |
| $-1$ | |
| $4$ | |
| $3$ |
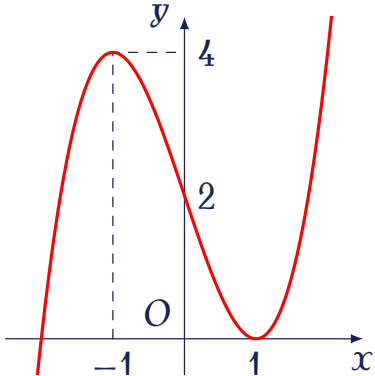
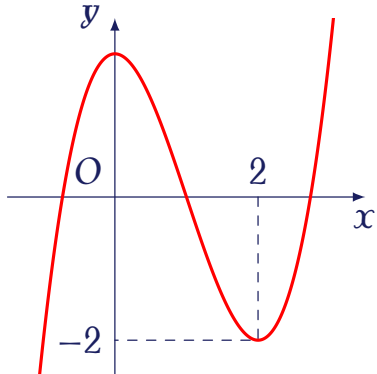
Hàm số nào sau đây có đồ thị như đường cong trong hình bên dưới?
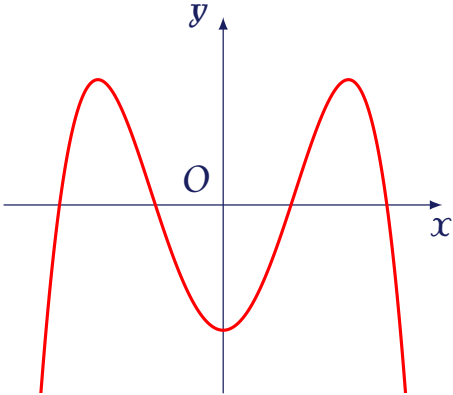
| $y=-x^4+3x^2-1$ | |
| $y=x^4-3x^2-1$ | |
| $y=x^3-x^2-1$ | |
| $y=-x^3+x^2-1$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{x+2022}{x+1}$ là
| $y=2022$ | |
| $y=-1$ | |
| $y=1$ | |
| $y=-2022$ |
Giá trị nhỏ nhất của hàm số $y=x^3+3x^2-1$ trên đoạn $[-1;1]$ bằng
| $3$ | |
| $-1$ | |
| $1$ | |
| $2$ |
Một xưởng in có $15$ máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in được $30$ ấn phẩm trong một giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho một đơn hàng là $48.000$ đồng, chi phí trả cho kỹ sư giám sát là $24.000$ đồng/giờ. Đợt hàng này xưởng in nhận $6000$ ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là
| $10$ máy | |
| $11$ máy | |
| $12$ máy | |
| $9$ máy |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ sau:
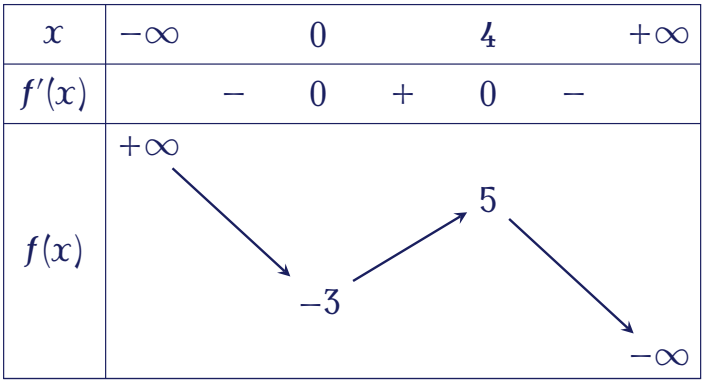
Giá trị lớn nhất của hàm số $g(x)=f\big(4x-x^2\big)+\dfrac{x^3}{3}-3x^2+8x+\dfrac{1}{3}$ trên đoạn $[1;3]$ bằng
| $15$ | |
| $\dfrac{25}{3}$ | |
| $\dfrac{19}{3}$ | |
| $12$ |
Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\big|3x^4-4x^3-12x^2+m\big|$ có $7$ điểm cực trị?
| $4$ | |
| $6$ | |
| $3$ | |
| $5$ |
Cho hàm số $y=f(x)$ xác thực trên tập số thực $\mathbb{R}$ và có đồ thị $f'(x)$ như hình vẽ.
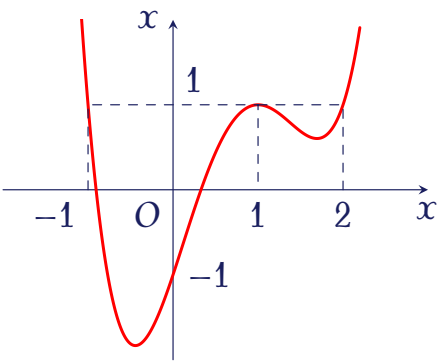
Đặt $g(x)=f(x)-x$, hàm số $g(x)$ nghịch biến trên khoảng
| $(1;+\infty)$ | |
| $(-1;2)$ | |
| $(2;+\infty)$ | |
| $(-\infty;-1)$ |
Cho hàm số $f(x)=x^4-32x^2+4$. Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, tổng giá trị các nghiệm phân biệt thuộc khoảng $(-3;2)$ của phương trình $f\big(x^2+2x+3\big)=m$ bằng $-4$?
| $145$ | |
| $142$ | |
| $144$ | |
| $143$ |
Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, hàm số $y=-x^3+3x^2-3mx+\dfrac{5}{3}$ có đúng một cực trị thuộc khoảng $(-2;5)$?
| $16$ | |
| $6$ | |
| $17$ | |
| $7$ |
