Cho 5 khẳng định sau về hình lăng trụ. Hỏi có bao nhiêu khẳng định đúng?

• Hình lăng trụ có tất cả các mặt bên đều là hình bình hành;
• Hình lăng trụ có 2 đáy là những đa giác bằng nhau và nằm trên 2 mặt phẳng song song;
• Hình lăng trụ có tất cả các cạnh bên song song và bằng nhau;
• Hình lăng trụ có 2 đáy đều là hình bình hành;
• Hình lăng trụ có tất cả các mặt bên đều là những hình chữ nhật.

	$4$
	$5$
	$3$
	$2$

Hai mặt phẳng $(P)$ và $(Q)$ thỏa mãn điều kiện nào sau đây thì $(P)$ và $(Q)$ song song với nhau?

	$(P)$ chứa 2 đường thẳng $a,\,b$ song song mà $a,\,b$ cùng song song với $(Q)$
	$(P)$ chứa 2 đường thẳng $a,\,b$ cắt nhau mà $a,\,b$ cùng song song với $(Q)$
	$(P)$ chứa 2 đường thẳng $a,\,b$ mà $a,\,b$ cùng song song với $(Q)$
	$(P)$ chứa 1 đường thẳng $a$ mà $a$ song song với $(Q)$

Cho hình chóp $S.ABC$. Gọi $M,\,N,\,P$ lần lượt là trung điểm của $SA,\,SB,\,SC$. Chọn khẳng định đúng.

	$(MNP)\parallel(ABC)$
	$(MNP)\parallel(SAC)$
	$(SMN)\parallel(ABC)$
	$(MNP)\parallel(SBC)$

Cho tứ diện $ABCD$. Gọi $N,\,K$ lần lượt là trung điểm các cạnh $BC$ và $CD$, $M$ là điểm trên cạnh $AB$ sao cho $MB=2MA$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là

	Hình bình hành
	Hình thang
	Hình chữ nhật
	Hình thoi

Cho tứ diện $ABCD$. Gọi $M,\,N,\,K$ lần lượt là trung điểm các cạnh $AB$, $BC$, $CD$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là

	Hình bình hành
	Hình thang
	Hình chữ nhật
	Hình thoi

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$ là đường thẳng

	Đi qua điểm $S$ và song song với $AD$
	Đi qua điểm $S$ và song song với $AB$
	Không tồn tại
	Đi qua giao điểm $I$ của $AB$ và $CD$

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Phát biểu nào không đúng về giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$?

	Song song với $CD$
	Đi qua điểm $S$
	Song song với $AB$
	Đi qua giao điểm $I$ của $AB$ và $CD$

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$

	Không tồn tại
	Đi qua điểm $S$
	Đi qua giao điểm $I$ của $AD$ và $BC$
	Đi qua giao điểm $I$ của $AB$ và $CD$

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

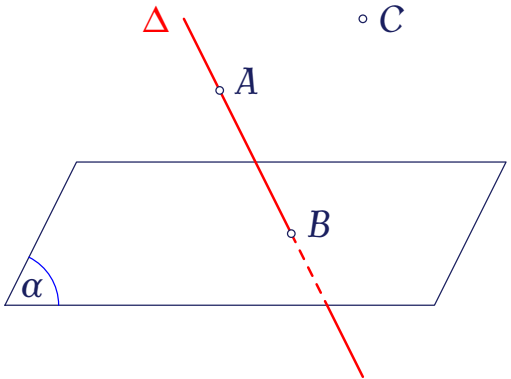
Giao tuyến của hai mặt phẳng $(\alpha)$ và $(ABC)$ có tồn tại không, nếu có thì giao tuyến đó đi qua điểm nào?

	$B$
	$A$
	$C$
	Không tồn tại

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

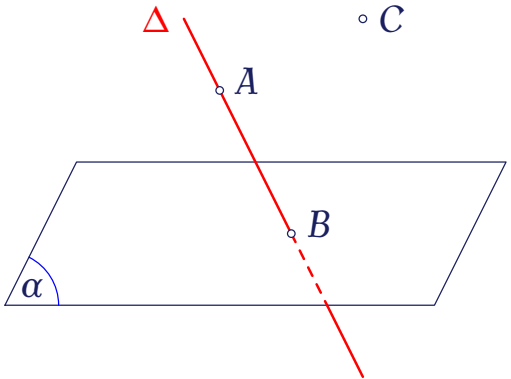
Mệnh đề nào sau đây là đúng?

	$\Delta\subset(\alpha)$
	$\Delta\cap(\alpha)=A$
	$C\in(\alpha)$
	$\Delta\cap(\alpha)=B$

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

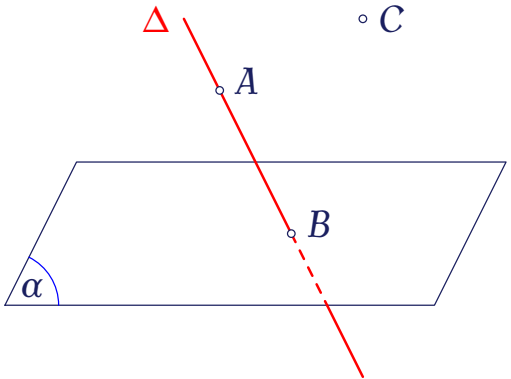
Xét mệnh đề "$B=\Delta\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.

	$\notin$
	$\in$
	$\subset$
	$\cap$

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

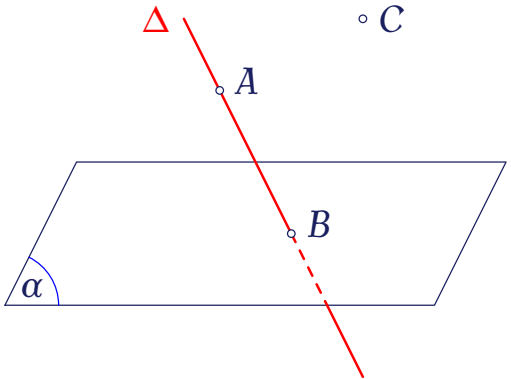
Xét mệnh đề "$C\ldots\ldots\Delta$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.

	$\notin$
	$\in$
	$\subset$
	$\cap$

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

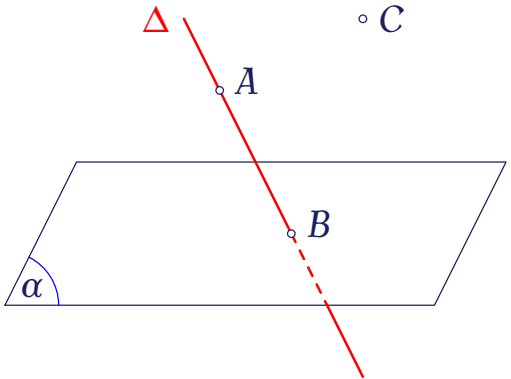
Xét mệnh đề "$A\ldots\ldots\Delta$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.

	$\notin$
	$\in$
	$\subset$
	$\cap$

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

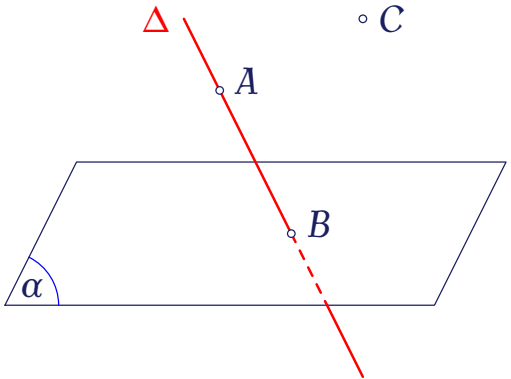
Xét mệnh đề "$A\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.

	$\notin$
	$\in$
	$\subset$
	$\cap$

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

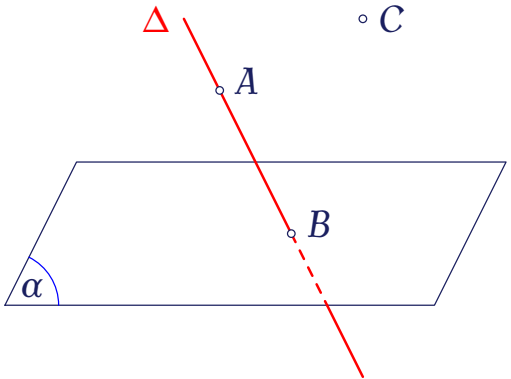
Xét mệnh đề "$B\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.

	$\notin$
	$\in$
	$\subset$
	$\cap$

Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.

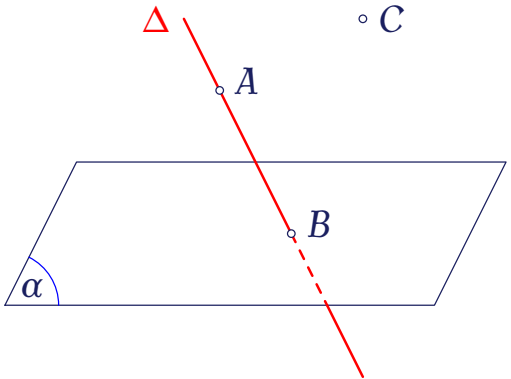
Phần nét đứt trong hình vẽ thể hiện điều gì?

	Phần không tồn tại
	Phần thấy được
	Phần không thấy được
	Phần bị ẩn

Cho tứ diện $ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $AC$ và $BC$. $P$ là điểm di động trên đoạn $BD$. Mặt phẳng $(MNP)$ cắt $AD$ tại $Q$.

1. Tứ giác $MNPQ$ là hình gì?
2. Tìm tập hợp giao điểm $I$ của $MQ$ và $NP$ khi $P$ di động trên đoạn $BD$.

Cho tứ diện $ABCD$, gọi $E$ là trung điểm của $AB$. Giao tuyến của hai mặt phẳng $(ECD)$ và $(ABC)$ là

	$ED$
	$EC$
	$EB$
	$EA$

Cho tứ diện $ABCD$, $M$ là trung điểm của $AB$, $N$ là điểm trên $AC$ mà $AN=\dfrac{1}{4}AC$, $P$ là điểm trên đoạn $AD$ mà $AP=\dfrac{2}{3}AD$. Gọi $E$ là giao điểm của $MP$ và $BD$, $F$ là giao điểm của $MN$ và $BC$. Khi đó giao tuyến của $(BCD)$ và $(MPC)$ là

	$CE$
	$MF$
	$NE$
	$CP$

Cho tứ diện $ABCD$. $M$ là điểm nằm trong tam giác $ABC$, $(\alpha)$ qua $M$ và song song với $AB$ và $CD$. Thiết diện của $ABCD$ cắt bởi $(\alpha)$ là

	Tam giác
	Hình bình hành
	Hình vuông
	Hình chữ nhật