Bảng biến thiên dưới đây mô tả sự biến thiên của hàm số nào?
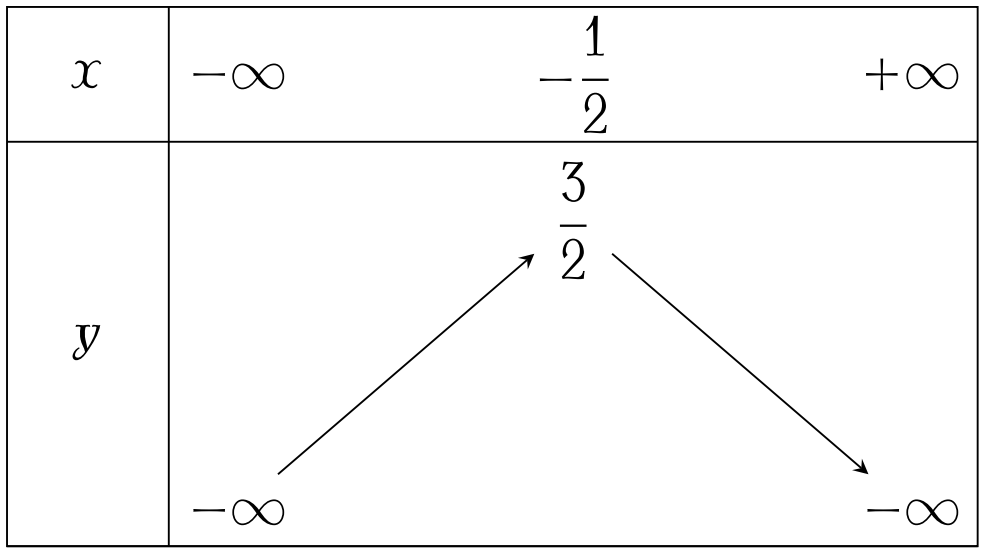
| $y=2x^2+2x-1$ | |
| $y=2x^2+2x+2$ | |
| $y=-2x^2-2$ | |
| $y=-2x^2-2x+1$ |
Bảng biến thiên dưới đây mô tả sự biến thiên của hàm số nào?
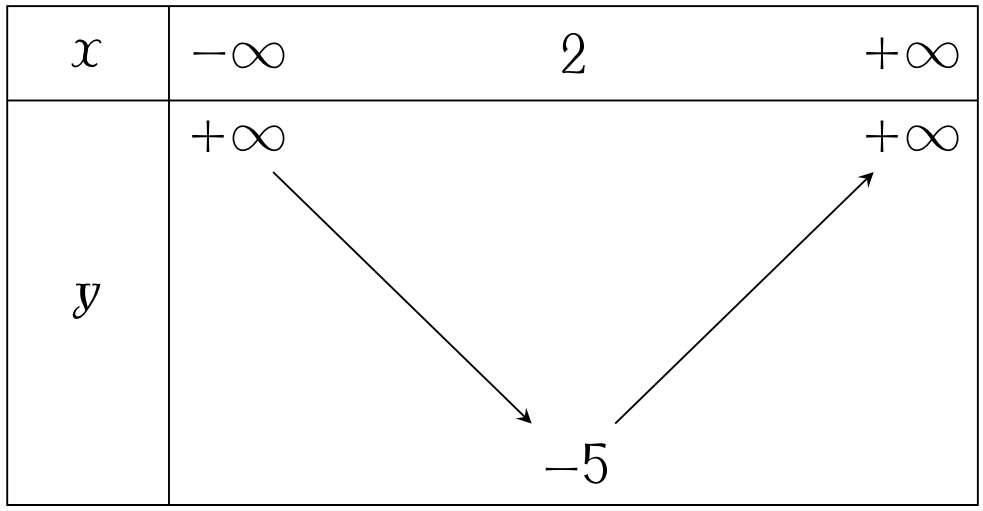
| $y=-x^2+4x-9$ | |
| $y=x^2-4x-1$ | |
| $y=-x^2+4x$ | |
| $y=x^2-4x-5$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
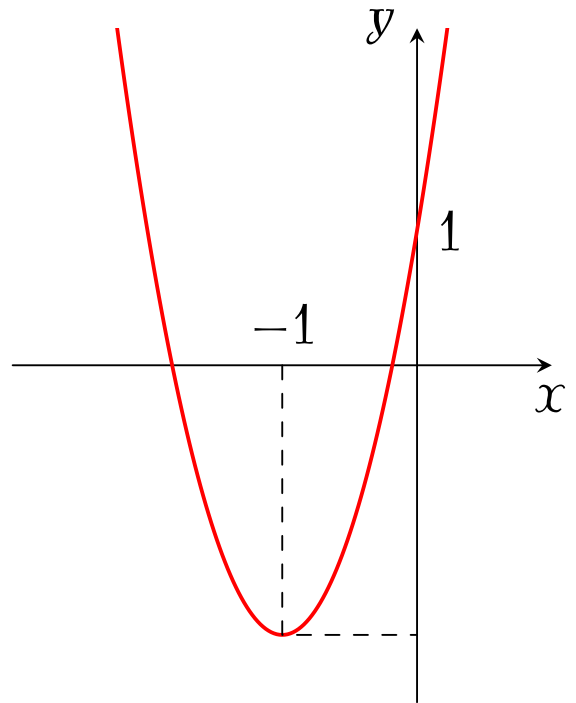
| $y=-3x^2-6x$ | |
| $y=3x^2+6x+1$ | |
| $y=x^2+2x+1$ | |
| $y=-x^2-2x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
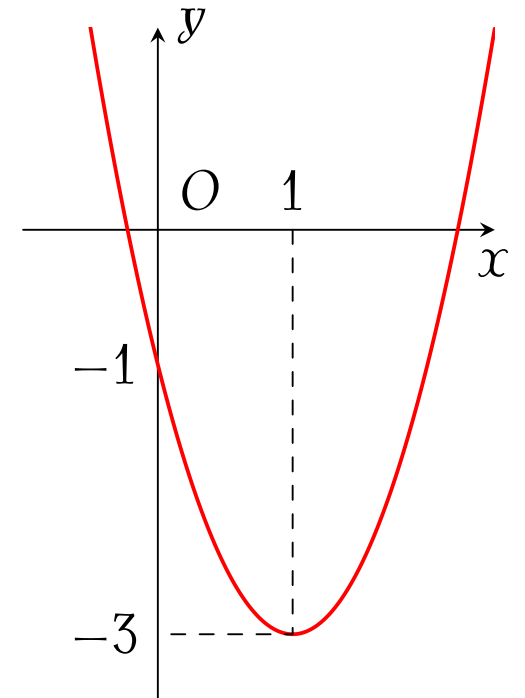
| $y=x^2-4x-1$ | |
| $y=2x^2-4x-1$ | |
| $y=-2x^2-4x-1$ | |
| $y=2x^2-4x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
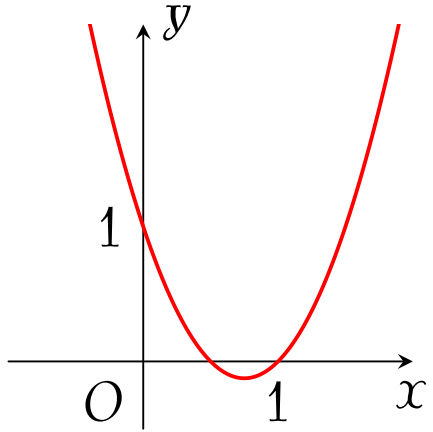
| $y=-x^2+3x-1$ | |
| $y=-2x^2+3x-1$ | |
| $y=2x^2-3x+1$ | |
| $y=x^2-3x+1$ |
Xác định parabol $\left(\mathscr{P}\right)\colon y=ax^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ đi qua ba điểm $A(1;1)$, $B(-1;-3)$ và $O(0;0)$.
| $y=x^2+2x$ | |
| $y=-x^2-2x$ | |
| $y=-x^2+2x$ | |
| $y=x^2-2x$ |
Xác định parabol $\left(\mathscr{P}\right)\colon y=2x^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ đi qua điểm $M(0;4)$ và có trục đối xứng $x=1$.
| $y=2x^2-4x+4$ | |
| $y=2x^2+4x-3$ | |
| $y=2x^2-3x+4$ | |
| $y=x^2-2x+3$ |
Xác định parabol $\left(\mathscr{P}\right)\colon y=ax^2+bx+2$, biết rằng $\left(\mathscr{P}\right)$ đi qua điểm $M(1;5)$ và $N(-2;8)$.
| $y=2x^2+x+2$ | |
| $y=x^2+x+2$ | |
| $y=-2x^2+x+2$ | |
| $y=-2x^2-x+2$ |
Hàm số nào sau đây đạt giá trị nhỏ nhất tại $x=\dfrac{3}{4}$?
| $y=4x^2-3x+1$ | |
| $y=-x^2+\dfrac{3}{2}x+1$ | |
| $y=-2x^2+3x+1$ | |
| $y=x^2-\dfrac{3}{2}x+1$ |
Tìm giá trị nhỏ nhất $m$ của hàm số $y=x^2-4x+5$.
| $m=0$ | |
| $m=-2$ | |
| $m=2$ | |
| $m=1$ |
Hàm số nào sau đây có đồ thị là parabol có đỉnh $I(-1;3)$?
| $y=2x^2-4x-3$ | |
| $y=2x^2-2x-1$ | |
| $y=2x^2+4x+5$ | |
| $y=2x^2+x+2$ |
Parabol $\left(\mathscr{P}\right)\colon y=3x^2-2x+1$ có đỉnh là
| $A\left(-\dfrac{1}{3};\dfrac{2}{3}\right)$ | |
| $B\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $C\left(\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $D\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ |
Cho hàm số $y=ax^2+bx+c$ $(a\neq0)$ có đồ thị $\left(\mathscr{P}\right)$. Tọa độ đỉnh của $\left(\mathscr{P}\right)$ là
| $I\left(-\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$ | |
| $I\left(-\dfrac{b}{a};-\dfrac{\Delta}{4a}\right)$ | |
| $I\left(-\dfrac{b}{2a};-\dfrac{\Delta}{4a}\right)$ | |
| $I\left(\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$ |
Đỉnh của parabol $\left(P\right)\colon y=3x^2-2x+1$ là
| $I\left(-\dfrac{1}{3};\dfrac{2}{3}\right)$ | |
| $J\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $K\left(\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $L\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ |
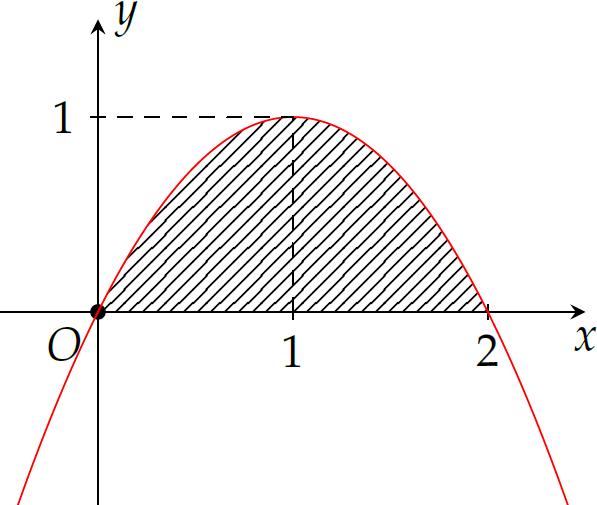
Cho hàm bậc hai \(y=f(x)\) có đồ thị như hình bên. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\) và \(Ox\) quanh \(Ox\).
| \(\dfrac{4\pi}{3}\) | |
| \(-\dfrac{12\pi}{15}\) | |
| \(\dfrac{16\pi}{15}\) | |
| \(\dfrac{16\pi}{5}\) |
Parabol \(y=x^2-x+3\) có đỉnh là
| \(A\left(\dfrac{1}{2};\dfrac{11}{4}\right)\) | |
| \(x=\dfrac{1}{2}\) | |
| \(B\left(-\dfrac{1}{2};\dfrac{15}{4}\right)\) | |
| \(I(1;3)\) |
Hàm số nào dưới đây có bảng biến thiên như sau?
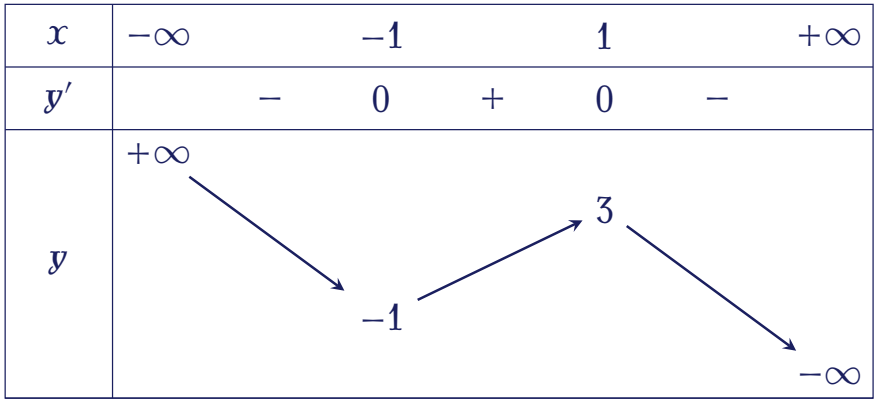
| $y=\dfrac{x+2}{x}$ | |
| $y=-x^3+3x+1$ | |
| $y=x^4-3x^2$ | |
| $y=-2x^2+1$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
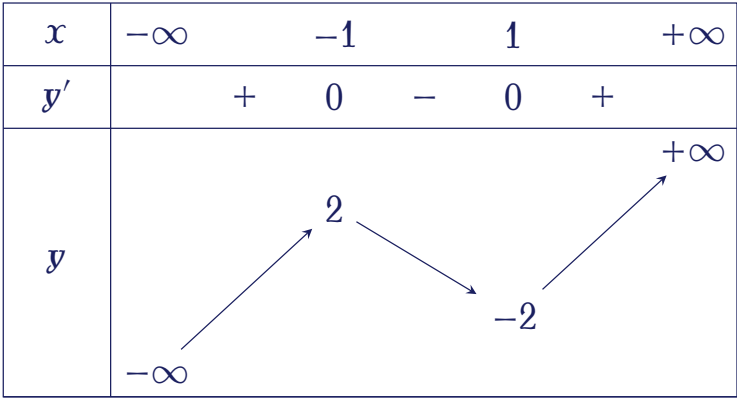
| $y=x^4-2x^2$ | |
| $y=-x^3+3x$ | |
| $y=-x^4+2x^2$ | |
| $y=x^3-3x$ |
Cho hàm số $y=x^2+4$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=2x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^2+4x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{x^3}{3}+4x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^3+4x+C$ |
