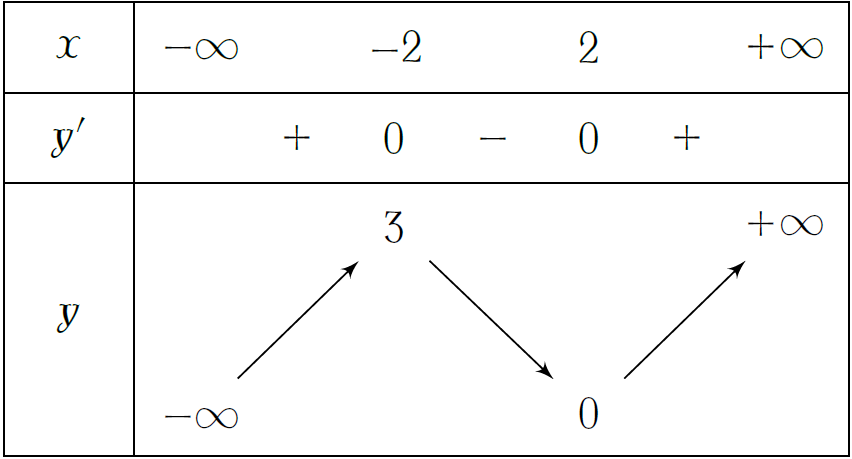
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình. Tìm giá trị cực đại \(y_{\text{CĐ}}\) và giá trị cực tiểu \(y_{\text{CT}}\) của hàm số đã cho.
| \(y_{\text{CĐ}}=-2\) và \(y_{\text{CT}}=2\) | |
| \(y_{\text{CĐ}}=3\) và \(y_{\text{CT}}=0\) | |
| \(y_{\text{CĐ}}=2\) và \(y_{\text{CT}}=0\) | |
| \(y_{\text{CĐ}}=3\) và \(y_{\text{CT}}=-2\) |
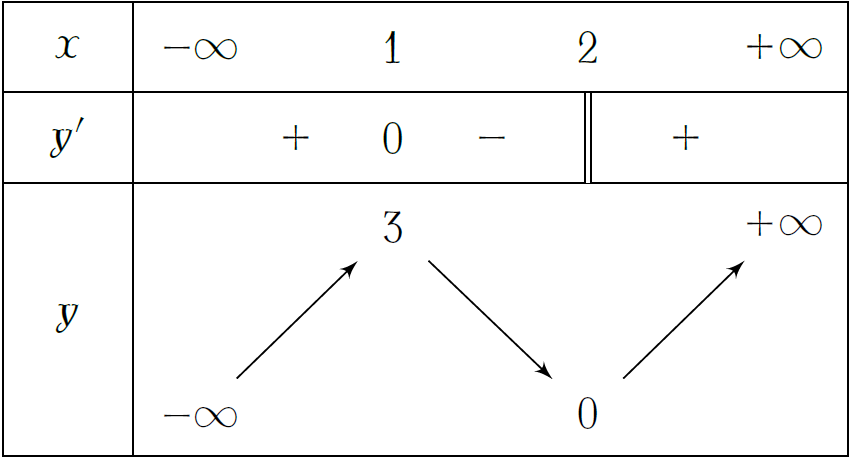
Hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?
| \(f(x)\) có \(2\) điểm cực trị | |
| \(f(x)\) có đúng \(1\) điểm cực trị | |
| \(f(x)\) không có giá trị cực tiểu | |
| \(f(x)\) không có giá trị cực đại |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
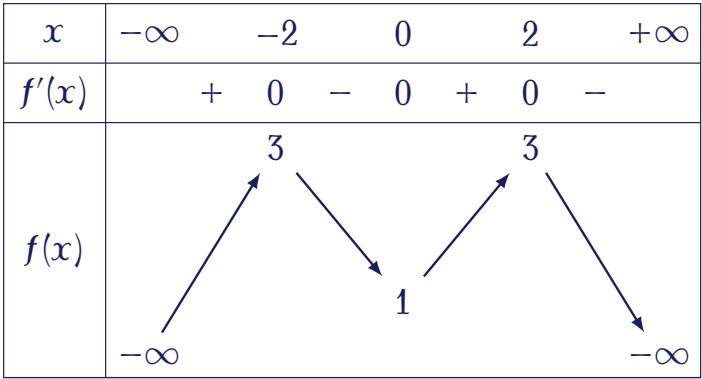
Số điểm cực tiểu của hàm số đã cho là
| $0$ | |
| $3$ | |
| $2$ | |
| $1$ |
Cho hàm số $f(x)$ có bảng biến thiên như sau:
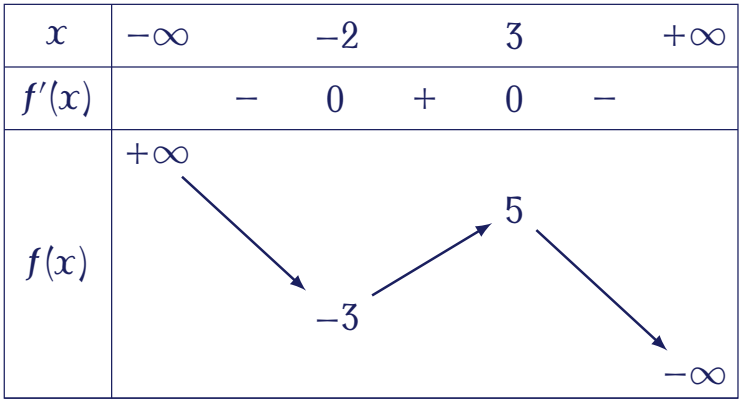
Hàm số đã cho đạt cực đại tại
| $x=-2$ | |
| $x=3$ | |
| $x=5$ | |
| $x=-3$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
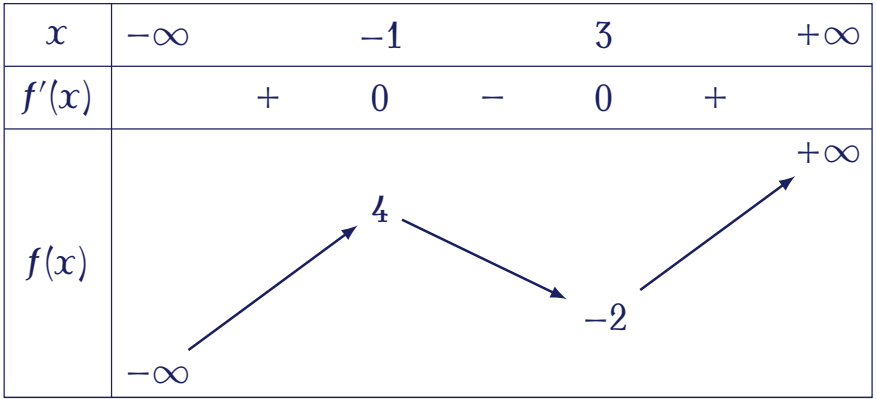
Giá trị cực đại của hàm số đã cho bằng
| $-2$ | |
| $-1$ | |
| $4$ | |
| $3$ |
Cho hàm số $f(x)$ có bảng biến thiên như sau:
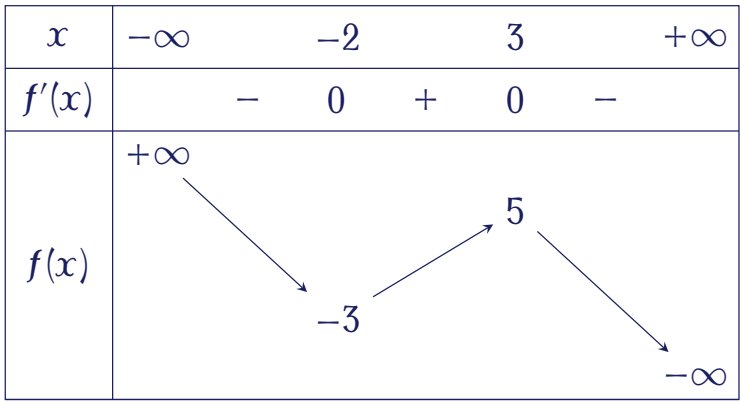
Hàm số đã cho đạt cực đại tại
| $x=-2$ | |
| $x=3$ | |
| $x=5$ | |
| $x=-3$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
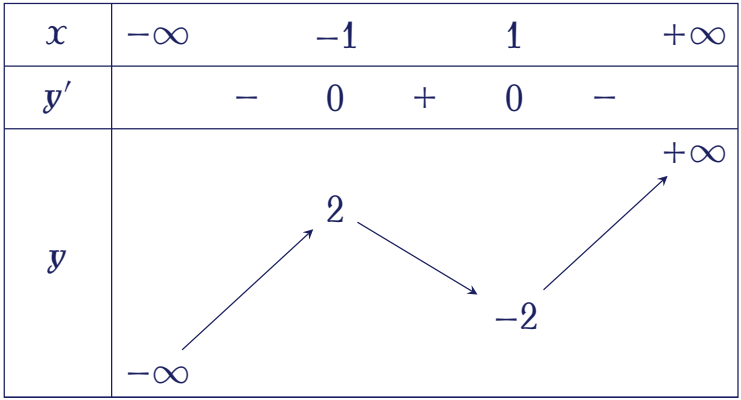
Điểm cực tiểu của hàm số đã cho là
| $x=-2$ | |
| $x=2$ | |
| $x=-1$ | |
| $x=1$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
| $-1$ | |
| $5$ | |
| $-3$ | |
| $1$ |
Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như hình bên.
Hàm số đã cho đạt cực tiểu tại
| $x=1$ | |
| $x=0$ | |
| $x=2$ | |
| $x=-2$ |
Cho hàm \(f\left(x\right)\) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
| \(3\) | |
| \(-5\) | |
| \(0\) | |
| \(2\) |
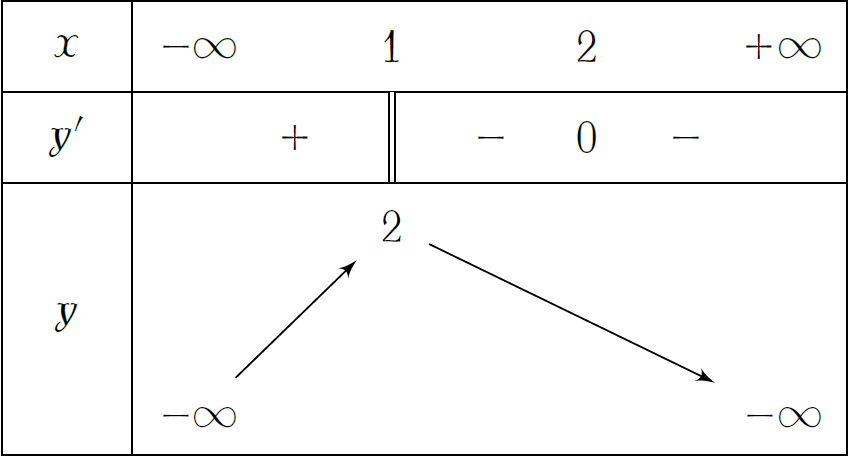
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
| Hàm số có giá trị cực đại bằng \(1\) | |
| Hàm số có đúng \(2\) cực trị | |
| Hàm số có giá trị cực đại bằng \(2\) | |
| Hàm số không xác định tại \(x=1\) |
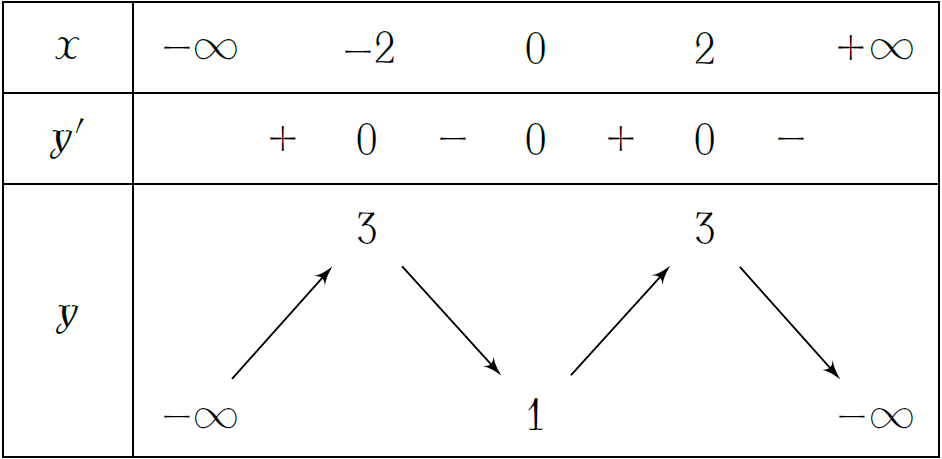
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Giá trị cực đại của hàm số bằng
| \(-2\) | |
| \(-1\) | |
| \(2\) | |
| \(3\) |
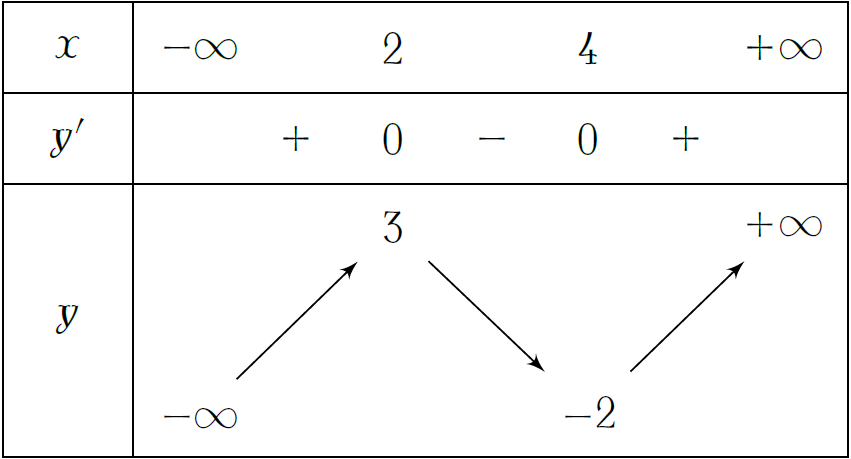
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Khẳng định nào sau đây là khẳng định đúng?
| Hàm số đạt cực đại tại \(x=2\) | |
| Hàm số đạt cực đại tại \(x=-2\) | |
| Hàm số đạt cực đại tại \(x=4\) | |
| Hàm số đạt cực đại tại \(x=3\) |
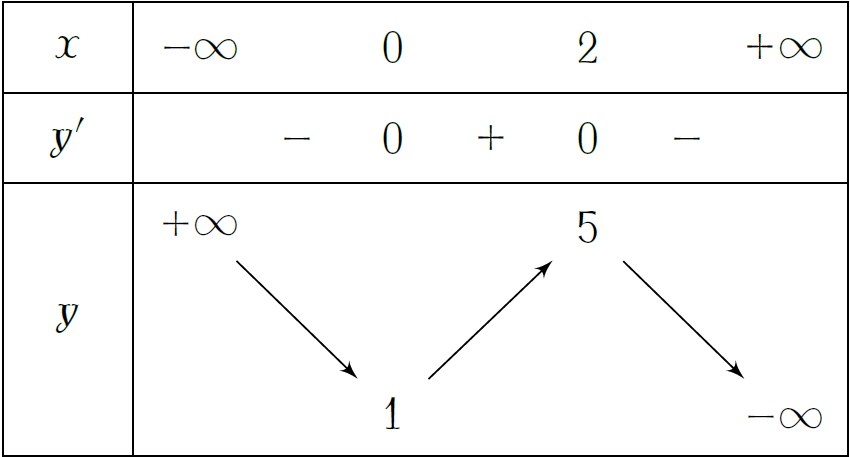
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Hàm số đạt cực tiểu tại điểm
| \(x=1\) | |
| \(x=5\) | |
| \(x=2\) | |
| \(x=0\) |
Cho hàm số \(y=f\left(x\right)\) có bảng biến thiên như sau:
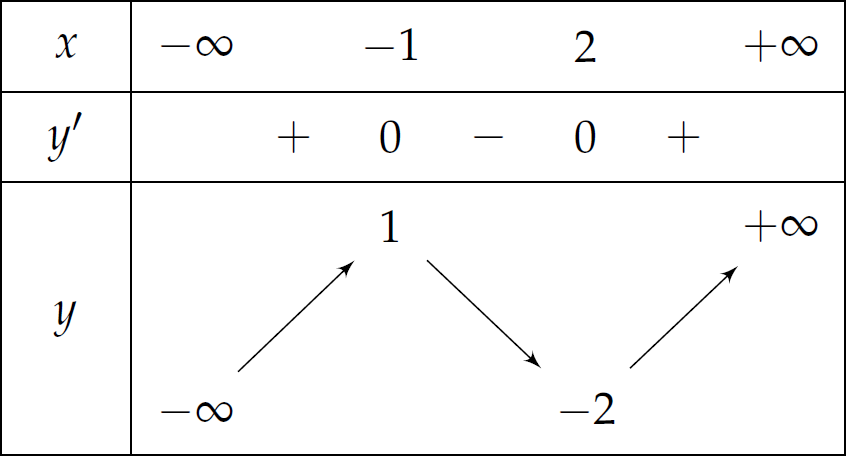
Hàm số đã cho đạt cực đại tại điểm
| \(x=-2\) | |
| \(x=2\) | |
| \(x=1\) | |
| \(x=-1\) |
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
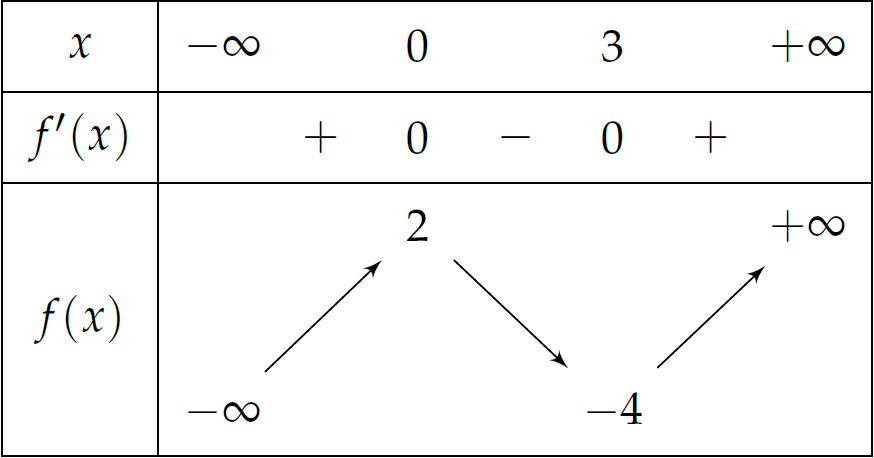
Giá trị cực tiểu của hàm số đã cho bằng
| \(2\) | |
| \(3\) | |
| \(0\) | |
| \(-4\) |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu $f'(x)$ như sau:

Hỏi hàm số $y=f\big(x^2-2x\big)$ có bao nhiêu điểm cực tiểu?
| $1$ | |
| $3$ | |
| $2$ | |
| $4$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Cho hàm số bậc bốn $y=f(x)$ có đồ thị là đường cong trong hình bên.
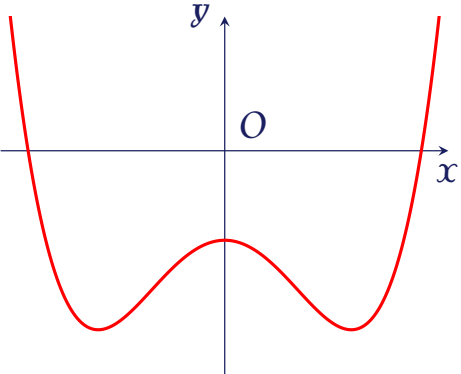
Số điểm cực tiểu của hàm số đã cho là
| $1$ | |
| $3$ | |
| $0$ | |
| $2$ |
Cho hàm số $y=ax^3+bx^2+cx+d$ $(a,b,c,d\in\mathbb{R})$ có đồ thị là đường cong trong hình bên.
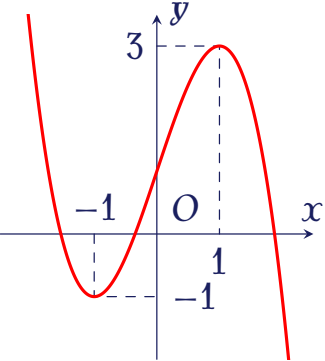
Giá trị cực đại của hàm số đã cho bằng
| $0$ | |
| $1$ | |
| $3$ | |
| $-1$ |
