Hình nào dưới đây biểu diễn cung lượng giác \(400^\circ\)?
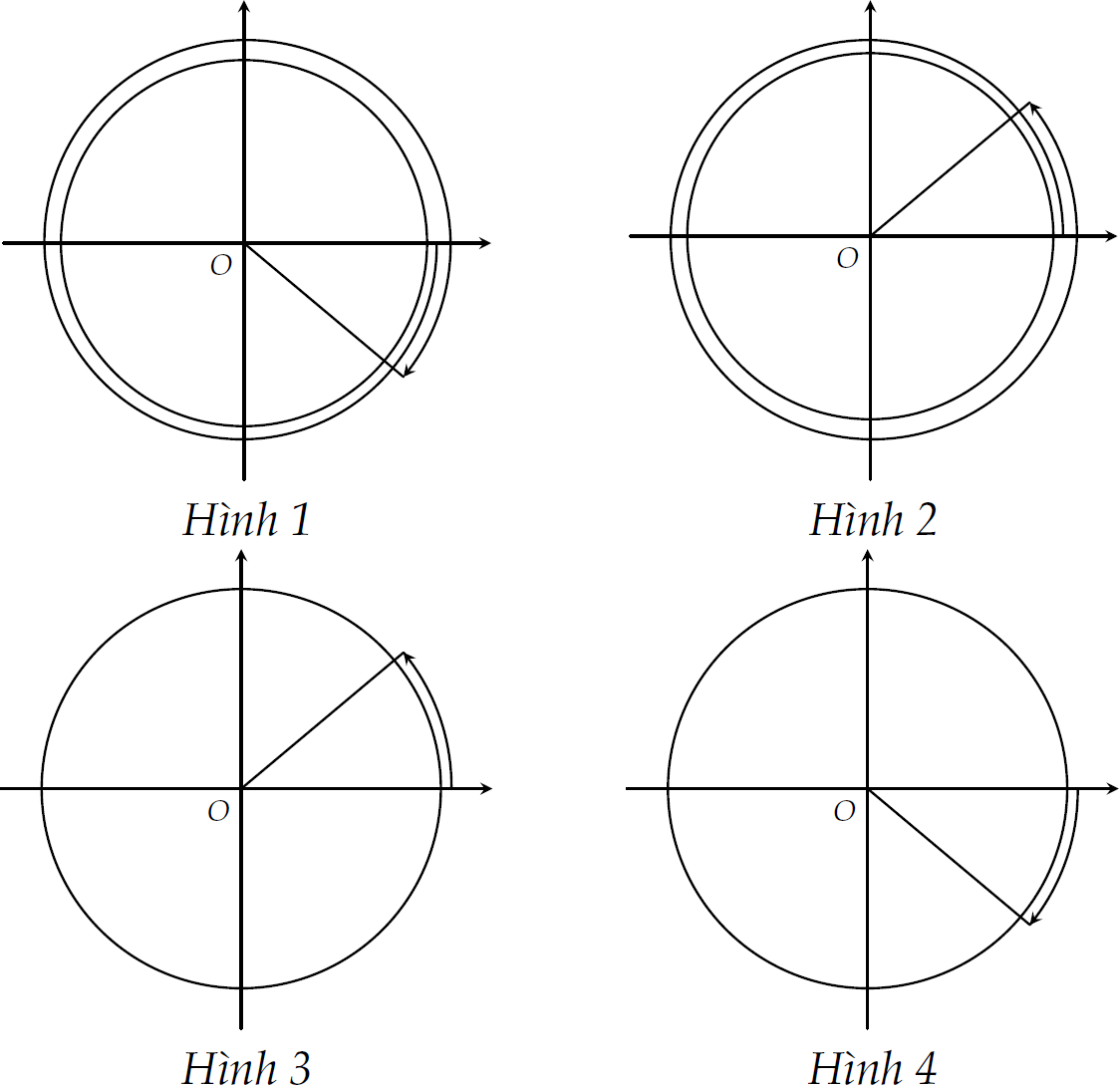
| Hình 1 | |
| Hình 3 | |
| Hình 4 | |
| Hình 2 |
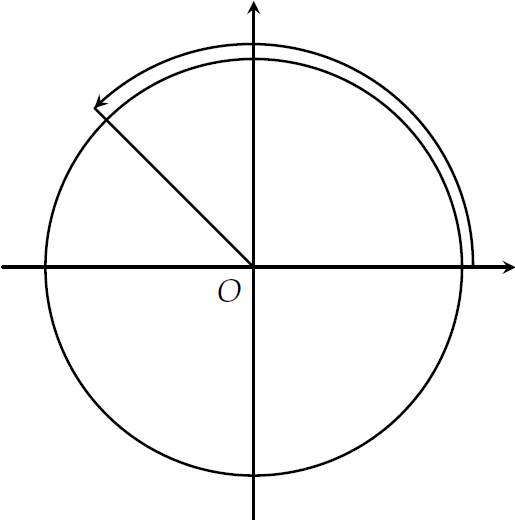
Hình trên mô tả cung tròn có số đo
| \(45^\circ\) | |
| \(135^\circ\) | |
| \(120^\circ\) | |
| \(150^\circ\) |
Khẳng định nào sau đây là đúng khi nói về "góc lượng giác"?
| Trên đường tròn tâm \(O\) bán kính \(R=1\), góc hình học \(AOB\) là góc lượng giác | |
| Trên đường tròn tâm \(O\) bán kính \(R=1\), góc hình học \(AOB\) có phân biệt điểm đầu \(A\) và điểm cuối \(B\) là góc lượng giác | |
| Trên đường tròn định hướng, góc hình học \(AOB\) là góc lượng giác | |
| Trên đường tròn định hướng, góc hình học \(AOB\) có phân biệt điểm đầu \(A\) và điểm cuối \(B\) là góc lượng giác |
Nghiệm của phương trình $\tan x=\tan\alpha$ là
| $x=\alpha+k3\pi,\,k\in\mathbb{Z}$ | |
| $x=\alpha+k2\pi,\,k\in\mathbb{Z}$ | |
| $x=\alpha$ | |
| $x=\alpha+k\pi,\,k\in\mathbb{Z}$ |
Phương trình $\sin x=\sin\alpha$ có nghiệm là
| $\left[\begin{array}{l}x=\alpha+k\pi\\ x=\pi-\alpha+k\pi\end{array}\right.$ | |
| $\left[\begin{array}{l}x=\alpha+k2\pi\\ x=-\alpha+k2\pi\end{array}\right.$ | |
| $\left[\begin{array}{l}x=\alpha+k\pi\\ x=-\alpha+k\pi\end{array}\right.$ | |
| $\left[\begin{array}{l}x=\alpha+k2\pi\\ x=\pi-\alpha+k2\pi\end{array}\right.$ |
Tìm nghiệm của phương trình $\cos x=1$.
| $x=\dfrac{\pi}{2}+k\pi\,(k\in\mathbb{Z})$ | |
| $x=k2\pi\,(k\in\mathbb{Z})$ | |
| $x=k\pi\,(k\in\mathbb{Z})$ | |
| $x=\pi+k\pi\,(k\in\mathbb{Z})$ |
Điều kiện có nghiệm của phương trình $a\sin x+b\cos x=c$ là
| $a^2+b^2>c^2$ | |
| $a^2+b^2\geq c^2$ | |
| $a^2+b^2\leq c^2$ | |
| $a^2+b^2< c^2$ |
Tìm công thức nghiệm của phương trình $\sin x=\sin\beta^{\circ}$ trong các công thức nghiệm sau đây:
| $\left[\begin{array}{l}x=\beta^{\circ}+k 180^{\circ}\\ x=180^{\circ}-\beta^{\circ}+k 180^{\circ}\end{array}\right.\;(k\in\mathbb{Z})$ | |
| $\left[\begin{array}{l}x=\beta^{\circ}+k 360^{\circ}\\ x=-\beta^{\circ}+k 360^{\circ}\end{array}\right.\;(k\in\mathbb{Z})$ | |
| $\left[\begin{array}{l}x=\beta^{\circ}+k 180^{\circ}\\ x=-\beta^{\circ}+k 180^{\circ}\end{array}\right.\;(k\in\mathbb{Z})$ | |
| $\left[\begin{array}{l}x=\beta^{\circ}+k 360^{\circ}\\ x=180^{\circ}-\beta^{\circ}+k 360^{\circ}\end{array}\right.\;(k\in\mathbb{Z})$ |
Phương trình $\sin x=0$ có nghiệm là
| $x=k\pi,\,k\in\mathbb{Z}$ | |
| $x=\dfrac{\pi}{4}+k\pi,\,k\in\mathbb{Z}$ | |
| $x=\dfrac{\pi}{2}+k 2\pi,\,k\in\mathbb{Z}$ | |
| $x=\dfrac{-\pi}{2}+k 2\pi,\,k\in\mathbb{Z}$ |
Mệnh đề nào sau đây là sai?
| $(\cos x)^{\prime}=-\sin x$ | |
| $(\sin x)^{\prime}=-\cos x$ | |
| $(\cot x)^{\prime}=-\dfrac{1}{\sin^2x}$ | |
| $(\tan x)^{\prime}=\dfrac{1}{\cos^2x}$ |
Cho hàm số $f(x)=\dfrac{1}{\cos^2x}$. Trong các khẳng định sau, khẳng định nào đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\tan x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\cot x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\cot x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\tan x+C$ |
Hàm số $y=\cot x$ có đạo hàm là
| $y'=-\dfrac{1}{\cos^2x}$ | |
| $y'=-\dfrac{1}{\sin^2x}$ | |
| $y'=\tan x$ | |
| $y'=\dfrac{1}{\sin^2x}$ |
Hàm số $y=\cos x$ có đạo hàm là
| $y'=\sin x$ | |
| $y'=\dfrac{1}{\sin x}$ | |
| $y'=-\cos x$ | |
| $y'=-\sin x$ |
Tính tích phân $I=\displaystyle\displaystyle\int\limits_{0}^{\pi}x^2\cos2x\mathrm{d}x$ bằng cách đặt $\begin{cases}u=x^2\\ \mathrm{d}v=\cos2x\mathrm{d}x\end{cases}$. Mệnh đề nào dưới đây đúng?
| $I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}-\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$ | |
| $I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}-2\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$ | |
| $I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}+2\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$ | |
| $I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}+\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$ |
Nguyên hàm $\displaystyle\displaystyle\int\sin x\mathrm{d}x$ là
| $-\cos x+C$ | |
| $\cos x+C$ | |
| $\dfrac{1}{2}\cos2x+C$ | |
| $-\cos2x+C$ |
Cho phương trình $a\sin x+b\cos x=c$ (với $a$, $b$, $c$ là các tham số). Tìm điều kiện cần và đủ của $a$, $b$, $c$ để phương trình có nghiệm.
| $a^2+b^2\ge c^2$ | |
| $a^2+b^2\le c^2$ | |
| $a+b\ge c$ | |
| $a+b\le c$ |
Nghiệm đặc biệt nào sau đây là sai?
| \(\sin x=0\Leftrightarrow x=k\pi\) | |
| \(\sin x=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\) | |
| \(\sin x=0\Leftrightarrow x=k\dfrac{\pi}{2}\) | |
| \(\sin x=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\) |
Trong các phương trình sau phương trình nào là phương trình bậc nhất đối với hàm số \(y=\sin x\)?
| \(2\cos x-1=0\) | |
| \(3\sin x+4=0\) | |
| \(\sqrt{3}\tan x-1=0\) | |
| \(2\sin3x+1=0\) |
Phương trình \(\cos x=1\) có họ nghiệm là
| \(x=\dfrac{\pi}{2}+k2\pi\,\left(k\in\mathbb{Z}\right)\) | |
| \(x=\dfrac{\pi}{2}+k\pi\,\left(k\in\mathbb{Z}\right)\) | |
| \(x=k2\pi\,\left(k\in\mathbb{Z}\right)\) | |
| \(x=k\pi\,\left(k\in\mathbb{Z}\right)\) |
Cho phương trình \(\sin x=a\). Biết rằng \(\sin\alpha=a\) và \(k\in\mathbb{Z}\). Khẳng định nào sau đây đúng?
| \(x=\pm\alpha+k2\pi\,\left(k\in\mathbb{Z}\right)\) | |
| \(\left[\begin{array}{l}x=\alpha+k2\pi\\ x=\pi-\alpha+k2\pi\end{array}\right.\,\left(k\in\mathbb{Z}\right)\) | |
| \(x=\alpha+k\pi\,\left(k\in\mathbb{Z}\right)\) | |
| \(x=\alpha+k2\pi\,\left(k\in\mathbb{Z}\right)\) |
