Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
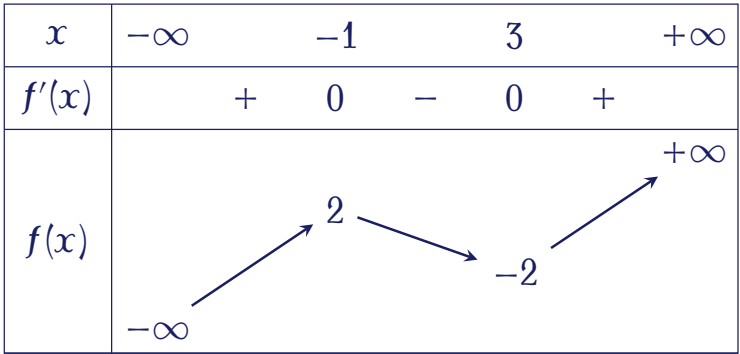
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(-\infty;2)$ | |
| $(1;+\infty)$ | |
| $(1;3)$ | |
| $(-\infty;1)$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $AC=4a$ và mặt bên $AA'B'B$ là hình vuông. Thể tích của khối lăng trụ $ABC.A'B'C'$ bằng
| $\dfrac{a^3}{8}$ | |
| $64a^3$ | |
| $\dfrac{a^3}{4}$ | |
| $32a^3$ |
Trên mặt phẳng tọa độ, điểm biểu diễn số phức $z=2+3i$ có tọa độ là
| $M(-2;3)$ | |
| $M(3;2)$ | |
| $M(2;-3)$ | |
| $M(2;3)$ |
Trong không gian $Oxyz$, cho mặt cầu $(S)\colon(x+1)^2+(y-3)^2+(z-2)^2=25$. Tâm $I$ và bán kính $R$ của mặt cầu $(S)$ là
| $I(-1;3;2),\,R=25$ | |
| $I(1;-3;-2),\,R=5$ | |
| $I(-1;3;2),\,R=5$ | |
| $I(1;-3;-2),\,R=25$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ bên.
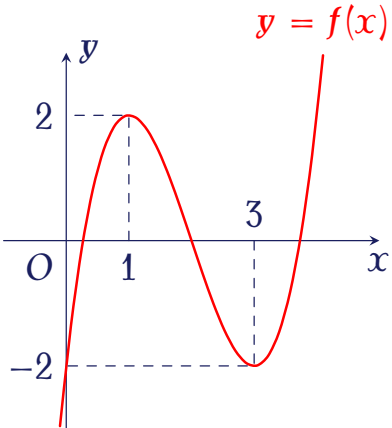
Hàm số đã cho đạt cực tiểu tại điểm
| $x=1$ | |
| $x=-2$ | |
| $x=2$ | |
| $x=3$ |
Nếu $\displaystyle\displaystyle\int\limits_0^3f(x)\mathrm{\,d}x=5$ và $\displaystyle\displaystyle\int\limits_0^1f(x)\mathrm{\,d}x=2$ thì $\displaystyle\displaystyle\int\limits_1^3f(x)\mathrm{\,d}x$ bằng
| $-3$ | |
| $3$ | |
| $10$ | |
| $7$ |
Nếu $\displaystyle\displaystyle\int\limits_1^3f(x)\mathrm{\,d}x=2$ thì $\displaystyle\displaystyle\int\limits_1^3\big[f(x)+4\big]\mathrm{\,d}x$ bằng
| $8$ | |
| $10$ | |
| $24$ | |
| $-2$ |
Cho tập hợp $A$ có $7$ phần tử. Số tập con gồm $3$ phần tử của tập hợp $A$ là
| $\mathrm{A}_7^3$ | |
| $3^7$ | |
| $\mathrm{C}_7^3$ | |
| $7^3$ |
Phần thực của số phức $z=4-6i$ là
| $-4$ | |
| $4$ | |
| $-6$ | |
| $6$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
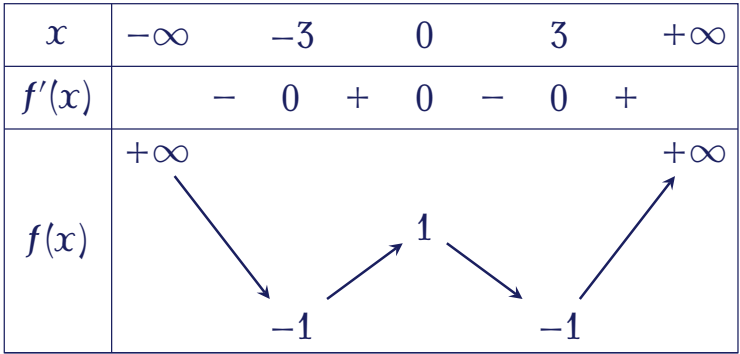
Số điểm cực trị của hàm số đã cho bằng
| $1$ | |
| $2$ | |
| $3$ | |
| $0$ |
Trong không gian $Oxyz$, đường thẳng $d\colon\begin{cases}x=1+2t\\ y=2-2t \\ z=-3-3t\end{cases}$ đi qua điểm nào dưới đây?
| $(1;2;3)$ | |
| $(2;2;3)$ | |
| $(1;2;-3)$ | |
| $(2;-2;-3)$ |
Cho hàm số $f(x)=2x-\mathrm{e}^x$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=2-\dfrac{\mathrm{e}^x}{\ln x}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^2-\mathrm{e}^x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=2-\mathrm{e}^x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^2+\mathrm{e}^x+C$ |
Xét số phức $z$ thỏa mãn $|z+3-2i|+|z-3+i|=3\sqrt{5}$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|+|z-1-3i|$. Khi đó
| $M=\sqrt{26}+2\sqrt{5}$, $m=3\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{26}+2\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=3\sqrt{2}$ |
Trong không gian $Oxyz$, cho hai điểm $M(1;2;3)$, $A(2;4;4)$ và hai mặt phẳng $(P)\colon x+y-2z+1=0$, $(Q)\colon x-2y-z+4=0$. Viết phương trình đường thẳng $\Delta$ đi qua $M$, cắt $(P)$, $(Q)$ lần lượt tại $B,\,C$ sao cho tam giác $ABC$ cân tại $A$ và nhận $AM$ làm đường trung tuyến.
| $\dfrac{x-1}{-1}=\dfrac{y-2}{-1}=\dfrac{z-3}{1}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{1}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}$ | |
| $\dfrac{x-1}{2}=\dfrac{y-2}{-1}=\dfrac{z-3}{1}$ |
Cho hai hàm số $f(x)=mx^3+nx^2+px-\dfrac{5}{2}$ $(m,\,n,\,p\in\mathbb{R})$ và $g(x)=x^2+2x-1$ có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là $-3$, $-1$, $1$ (tham khảo hình vẽ).
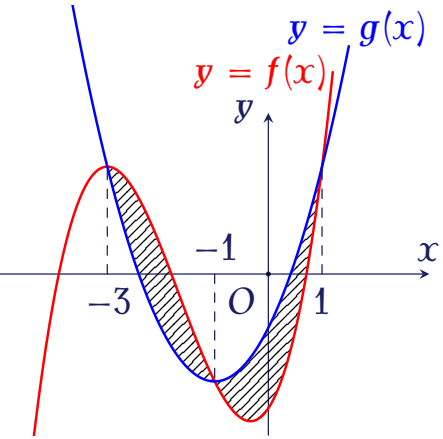
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $f(x)$ và $g(x)$ bằng
| $\dfrac{9}{2}$ | |
| $\dfrac{18}{5}$ | |
| $4$ | |
| $5$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $2f(x)+f'(x)=2x+1$, $\forall x\in\mathbb{R}$ và $f(0)=1$. Giá trị của $\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$ bằng
| $1-\dfrac{1}{2\mathrm{e}^2}$ | |
| $1+\dfrac{1}{2\mathrm{e}^2}$ | |
| $\dfrac{1}{2\mathrm{e}^2}$ | |
| $-\dfrac{1}{2\mathrm{e}^2}$ |
Biết $F(x)$ và $G(x)$ là hai nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$ và $\displaystyle\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=F(3)-G(0)+a$ ($a>0$). Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=F(x)$, $y=G(x)$, $x=0$ và $x=3$. Khi $S=15$ thì $a$ bằng
| $15$ | |
| $12$ | |
| $18$ | |
| $5$ |
Cho hàm số $f(x)=\begin{cases} x^2+3 &\text{với }x\geq1\\ 5-x &\text{với }x< 1 \end{cases}$. Tính $$I=2\displaystyle\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}f(\sin x)\cos x\mathrm{\,d}x+3\displaystyle\int\limits_{0}^{1}f(3-2x)\mathrm{\,d}x.$$
| $I=\dfrac{32}{3}$ | |
| $I=32$ | |
| $I=\dfrac{71}{6}$ | |
| $I=31$ |
Cho hàm số $f(x)$ có đạo hàm $f'(x)$ liên tục trên $\mathbb{R}$ và thỏa mãn $\displaystyle\displaystyle\int\limits_{0}^{1}(3x+1)f'(x)\mathrm{\,d}x=2022$ và $4f(1)-f(0)=2028$. Giá trị của $I=\displaystyle\displaystyle\int\limits_{0}^{\tfrac{1}{4}}f(4x)\mathrm{\,d}x$ là
| $2$ | |
| $\dfrac{2022}{3}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{1}{4}$ |
Gọi $V$ là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y=\sqrt{x}$, $y=0$ và $x=4$ quanh trục $Ox$. Đường thẳng $x=a$ ($0< a< 4$) cắt đồ thị hàm số $y=\sqrt{x}$ tại $M$ (tham khảo hình vẽ).
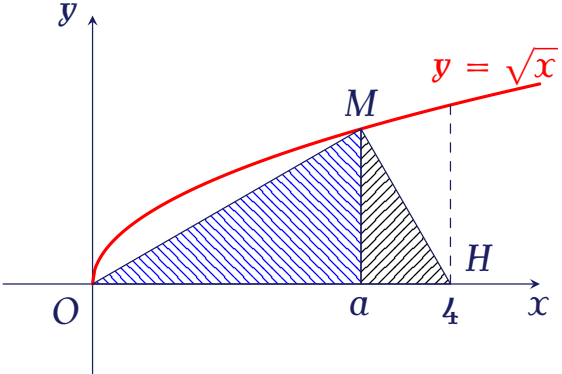
Gọi $V_1$ là thể tích khối tròn xoay tạo thành khi quay tam giác $OMH$ quanh trục $Ox$. Biết rằng $V=2V_1$. Khi đó
| $a=3$ | |
| $a=2\sqrt{2}$ | |
| $a=\dfrac{5}{2}$ | |
| $a=2$ |
