Điểm cực tiểu của đồ thị hàm số \(y=-x^3+x^2+5x-5\) là điểm nào?

	\((-1;-8)\)
	\((1;0)\)
	\((0;-5)\)
	\(\left(\dfrac{5}{3};\dfrac{40}{27}\right)\)

Đồ thị sau đây là của hàm số \(y=x^3-3x+1\).

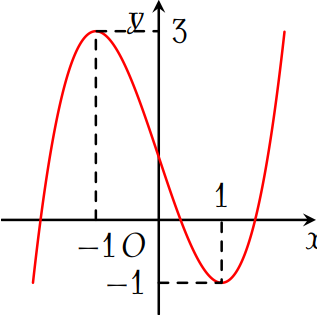
Với giá trị nào của \(m\) thì phương trình \(x^3-3x-m=0\) có \(3\) nghiệm phân biệt?

	\(-2< m<2\)
	\(-2< m<3\)
	\(-1< m<3\)
	\(-2\leq m<2\)

Cho hàm số \(y=f(x)\) có đạo hàm trên khoảng \(\mathbb{K}\). Mệnh đề nào dưới đây đúng?

	Nếu \(f'(x)\geq0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)\leq0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)<0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)>0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)

Biết rằng đường thẳng \(y=4x+5\) cắt đồ thị hàm số \(y=x^3+2x+1\) tại điểm duy nhất, kí hiệu \(\left(x_0;y_0\right)\) là tọa độ của điểm đó. Tìm \(y_0\).

	\(y_0=11\)
	\(y_0=10\)
	\(y_0=13\)
	\(y_0=12\)

Hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có bảng biến thiên như sau:

Gọi \(M\) là giá trị lớn nhất của hàm số \(y=f(x)\) trên đoạn \([-1;3]\). Khẳng định nào sau đây là khẳng định đúng?

	\(M=f(0)\)
	\(M=f(3)\)
	\(M=f(2)\)
	\(M=f(-1)\)

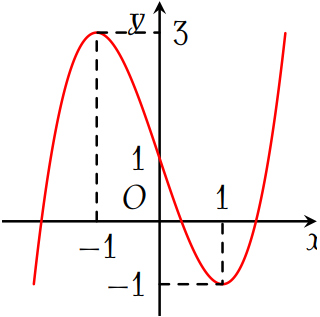
Đường cong trong hình vẽ là đồ của hàm số nào dưới đây?

	\(y=x^3-3x+3\)
	\(y=x^3-3x\)
	\(y=x^3-3x+1\)
	\(y=-x^3+3x+1\)

Hàm số nào sau đây không có điểm cực trị?

	\(y=-x^4+2x^2-5\)
	\(y=x^4+2x^2-5\)
	\(y=-\dfrac{1}{4}x^4+6\)
	\(y=x^3+6x-2019\)

Nếu hàm số \(y=f(x)\) thỏa mãn \(\lim\limits_{x\to1^-}f(x)=-\infty\) thì đồ thị hàm số \(y=f(x)\) có đường tiệm cận đứng là đường thẳng có phương trình

	\(x=-1\)
	\(x=1\)
	\(y=1\)
	\(y=-1\)

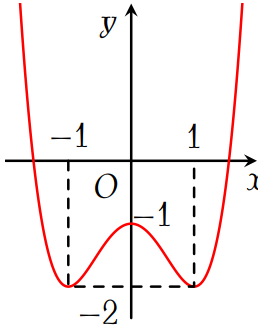
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng

	\(1\)
	\(-2\)
	\(-1\)
	\(0\)

Tập xác định \(\mathscr{D}\) của hàm số \(y=(x+1)^{\tfrac{1}{3}}\) là

	\(\mathscr{D}=\mathbb{R}\setminus\{-1\}\)
	\(\mathscr{D}=(-1;+\infty)\)
	\(\mathscr{D}=\mathbb{R}\)
	\(\mathscr{D}=(-\infty;-1)\)

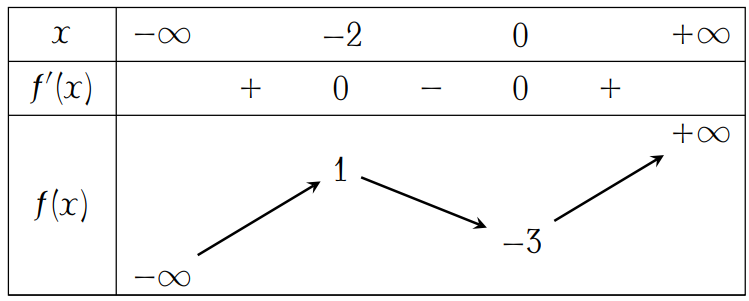
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Hàm số nghịch biến trên khoảng nào dưới đây?

	\((-\infty;-2)\)
	\((0;+\infty)\)
	\((1;-3)\)
	\((-2;0)\)

Dựa vào đồ thị của hàm số \(y=\sin x\). Tìm giá trị lớn nhất của hàm số trên \(\left[-\pi;-\dfrac{\pi}{2}\right]\).

	\(1\)
	\(0\)
	\(-1\)
	\(\dfrac{1}{2}\)

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\cos2x-2\) lần lượt là

	\(-3\) và \(-1\)
	\(3\) và \(-2\)
	\(2\) và \(-2\)
	\(3\) và \(-1\)

Tập xác định của hàm số \(y=\dfrac{\cot x}{\sin x-1}\) là

	\(\mathscr{D}=\mathbb{R}\setminus\left\{k\dfrac{\pi}{2}\bigg|k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{3}+k2\pi\bigg|k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi\bigg|k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi;\,k\pi\bigg|k\in\mathbb{Z}\right\}\)

Tập xác định của hàm số \(y=\tan x\) là

	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi\,k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi\,k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{k\pi\,k\in\mathbb{Z}\right\}\)

Điều kiện xác định của hàm số \(y=\dfrac{1-\cos x}{\sin x}\) là

	\(x\ne\dfrac{\pi}{2}+k\pi\)
	\(x\ne k\pi\)
	\(x\ne-\dfrac{\pi}{2}+k2\pi\)
	\(x\ne\dfrac{\pi}{2}+k2\pi\)

Hàm số \(y=\sin x\cos^3x\) là

	Hàm số lẻ
	Hàm số chẵn
	Hàm số không chẵn
	Hàm số không lẻ

Cho \(x,\,y\) là hai số không âm thỏa mãn \(x+y=2\). Tìm giá trị nhỏ nhất của biểu thức $$P=\dfrac{x^3}{3}+x^2+y^2-x+1$$

	\(\dfrac{17}{3}\)
	\(5\)
	\(\dfrac{115}{3}\)
	\(\dfrac{7}{3}\)

Một chất điểm chuyển động theo phương trình \(S=-2t^3+18t^2+1\), trong đó \(t\) tính bằng giây và \(S\) tính bằng mét. Mất bao lâu kể từ lúc xuất phát để chất điểm đạt vận tốc lớn nhất?

	\(5\) giây
	\(6\) giây
	\(3\) giây
	\(1\) giây

Một xưởng sản xuất cần làm \(100\) chiếc hộp inox bằng nhau, hình dạng là hình hộp chữ nhật có đáy là hình vuông (không có nắp), với thể tích là \(108\) dm\(^3\)/hộp. Giá của inox là \(47.000\) đồng/dm\(^2\). Hãy tính toán sao cho tổng chi phí sản xuất \(100\) chiếc hộp là ít nhất, và số tiền tối thiểu đó là bao nhiêu (nếu chỉ tính số inox vừa đủ để sản xuất \(100\) chiếc hộp, không có phần dư thừa, cắt bỏ)?

	\(1.692.000.000\) đồng
	\(507.666.000\) đồng
	\(1.015.200.000\) đồng
	\(235.800.000\) đồng