Một trang trại mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau với giá \(30000\) đồng/kg thì hết sạch rau, nếu giá bán cứ tăng thêm \(1000\) đồng/kg thì số rau thừa lại tăng thêm \(20\) kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá \(2000\) đồng/kg. Hỏi số tiền bán rau nhiều nhất mà trang trại có thể thu được mỗi ngày là bao nhiêu?
| \(32.420.000\) đồng | |
| \(32.400.000\) đồng | |
| \(34.400.000\) đồng | |
| \(34.240.000\) đồng |
Một xưởng in có $15$ máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in được $30$ ấn phẩm trong một giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho một đơn hàng là $48.000$ đồng, chi phí trả cho kỹ sư giám sát là $24.000$ đồng/giờ. Đợt hàng này xưởng in nhận $6000$ ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là
| $10$ máy | |
| $11$ máy | |
| $12$ máy | |
| $9$ máy |
Một chất điểm chuyển động theo quy luật $S=-\dfrac{1}{3}t^3+4t^2+\dfrac{2}{3}$ với $t$(giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và $S$(mét) là quãng đường vật chuyển động trong thời gian đó. Hỏi trong khoảng thời gian $8$ giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của chất điểm là bao nhiêu?
| $86$(m/s) | |
| $16$(m/s) | |
| $\dfrac{2}{3}$(m/s) | |
| $43$(m/s) |
Một vật chuyển động theo quy luật $s=-\dfrac{1}{2}t^3+6t^2$ với $t$ (giây) là khoảng thời gian từ khi vật bắt đầu chuyển động và $s$ (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian $6$ giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?
| $24$(m/s) | |
| $108$(m/s) | |
| $64$(m/s) | |
| $18$(m/s) |
Một chất điểm chuyển động theo phương trình \(S=-2t^3+18t^2+1\), trong đó \(t\) tính bằng giây và \(S\) tính bằng mét. Mất bao lâu kể từ lúc xuất phát để chất điểm đạt vận tốc lớn nhất?
| \(5\) giây | |
| \(6\) giây | |
| \(3\) giây | |
| \(1\) giây |
Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển \(BC=5\) km. Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) \(7\) km. Người gác hải đăng có thể chèo đò từ \(A\) đến vị trí \(M\) trên bờ biển với vận tốc \(4\) km/h rồi đi bộ đến \(C\) với vận tốc \(6\) km/h.

Vị trí của điểm \(M\) phải cách \(B\) bao nhiêu km để người gác hải đăng đến \(C\) nhanh nhất?
| \(0\) km | |
| \(\dfrac{14+5\sqrt{5}}{12}\) km | |
| \(2\sqrt{5}\) km | |
| \(7\) km |
Cho hai cây cột có chiều cao lần lượt là $6$m, $15$m và đặt cách nhau $20$m (như hình minh họa).
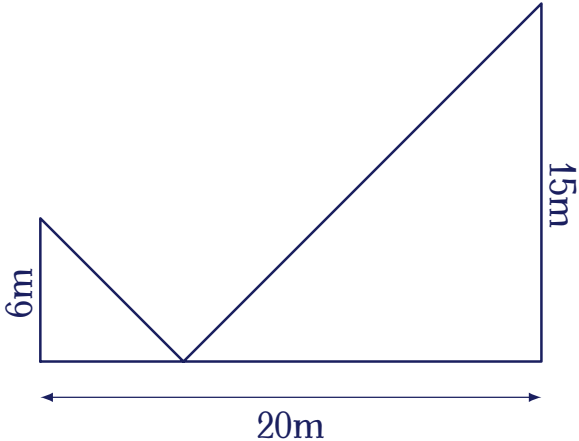
Một sợi dây dài được gắn vào đỉnh của mỗi cột và được đóng cọc xuống đất tại một điểm ở giữa hai cột. Chiều dài sợi dây được sử dụng ít nhất là
| $30$m | |
| $29$m | |
| $31$m | |
| $28$m |
Giá trị nhỏ nhất của hàm số $y=x^3+3x^2-1$ trên đoạn $[-1;1]$ bằng
| $3$ | |
| $-1$ | |
| $1$ | |
| $2$ |
Cho $x,\,y$ là các số thực thỏa mãn $(x-3)^2+(y-1)^2=5$. Giá trị nhỏ nhất của biểu thức $P=\dfrac{3y^2+4xy+7x+4y-1}{x+2y+1}$ là
| $2\sqrt{3}$ | |
| $\dfrac{114}{11}$ | |
| $\sqrt{3}$ | |
| $3$ |
Cho $x,\,y$ là hai số thực bất kì thuộc đoạn $[1;3]$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $S=\dfrac{x}{y}+\dfrac{y}{x}$. Tính $M+m$.
| $M+m=\dfrac{10}{3}$ | |
| $M+m=\dfrac{16}{3}$ | |
| $M+m=3$ | |
| $M+m=5$ |
Cho hai số thực $x,\,y$ thay đổi thỏa mãn điều kiện $x^2+y^2=2$. Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=2\big(x^3+y^3\big)-3xy$. Giá trị của $M+m$ bằng
| $-4$ | |
| $-\dfrac{1}{2}$ | |
| $-6$ | |
| $1-4\sqrt{2}$ |
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$, đồ thị của hàm số $y=f'(x)$ như hình vẽ.
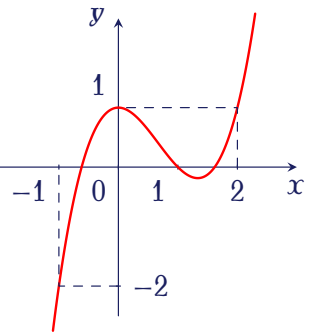
Giá trị lớn nhất của hàm số $g(x)=2f(x)-(x-1)^2$ trên đoạn $[-1;2]$ bằng
| $2f(0)-1$ | |
| $2f(-1)-4$ | |
| $2f(1)$ | |
| $2f(2)-1$ |
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ có đồ thị $y=f'(x)$ cho như hình vẽ.
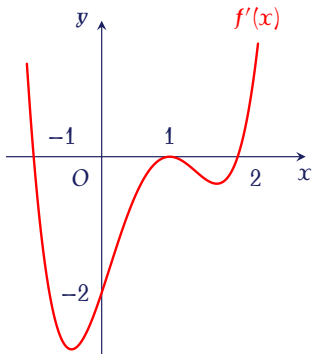
Giá trị nhỏ nhất của hàm số $y=f(x)+\dfrac {1}{3}x^3-x$ trên đoạn $[-1;2]$ bằng
| $f(2)+\dfrac{2}{3}$ | |
| $f(-1)+\dfrac{2}{3}$ | |
| $\dfrac{2}{3}$ | |
| $f(1)-\dfrac{2}{3}$ |
Cho hàm số $f(x)$ có đồ thị $f'(x)$ như hình vẽ.
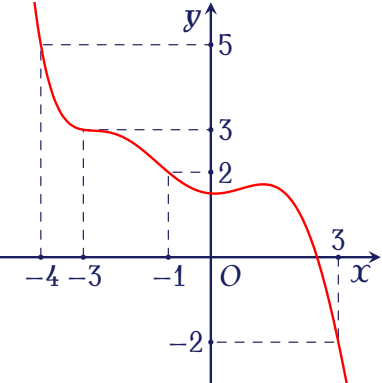
Trên đoạn $[-4;3]$, hàm số $g(x)=2f(x)+(1-x)^2$ đạt giá trị nhỏ nhất tại điểm
| $x_0=-4$ | |
| $x_0=-1$ | |
| $x_0=3$ | |
| $x_0=-3$ |
Cho hàm số $y=f(x)$. Đồ thị của hàm số $y=f'(x)$ như hình vẽ.
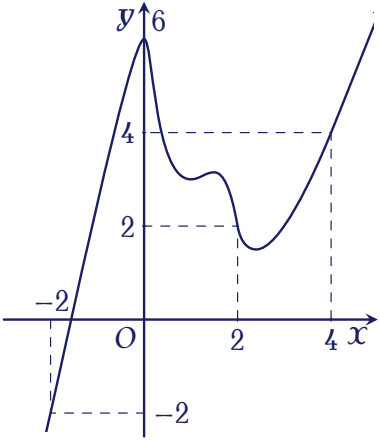
Đặt $h(x)=f(x)-x$. Mệnh đề nào dưới đây đúng?
| $\min\limits_{[-2;2]}h(x)=h(-2)$ | |
| $\max\limits_{[0;4]}h(x)=h(0)$ | |
| $\min\limits_{[-1;2]}h(x)=h(-1)$ | |
| $h(2)< h(4)< h(0)$ |
Tìm giá trị nhỏ nhất của tham số $m$ để bất phương trình $$\dfrac{x^3+\sqrt{3x^2+1}+1}{\sqrt{x}-\sqrt{x-1}}\leq\dfrac{m}{\left(\sqrt{x}+\sqrt{x-1}\right)^2}$$có nghiệm.
| $m=1$ | |
| $m=4$ | |
| $m=13$ | |
| $m=8$ |
Tìm $m$ sao cho bất phương trình $\dfrac{x^2-2x+2}{x-1}\leq m$ có đúng một nghiệm trên khoảng $(1;+\infty)$.
| $m\geq2$ | |
| $m\leq2$ | |
| $m=2$ | |
| $m>2$ |
Cho hàm số $f(x)=\dfrac{x+m}{x+1}$ với $m$ là tham số thực. Tìm giá trị của $m$ thỏa mãn $\min\limits_{[1;2]}f(x)+\min\limits_{[1;2]}f(x)=\dfrac{16}{3}$.
| $m=5$ | |
| $m=\dfrac{5}{6}$ | |
| $m=-5$ | |
| $m=\dfrac{5}{3}$ |
Cho hàm số $f(x)=\dfrac{x+m}{x-1}$ với $m$ là tham số thực. Gọi $m$ là giá trị thỏa mãn $\min\limits_{[2;4]}=3$, mệnh đề nào sau đây là đúng?
| $3< m\leq4$ | |
| $1\leq m<3$ | |
| $m>4$ | |
| $m<-1$ |
Cho hàm số $f(x)=\dfrac{x-m^2}{x+8}$ với $m$ là tham số thực. Tìm giá trị lớn nhất của $m$ để hàm số có giá trị nhỏ nhất trên đoạn $[0;3]$ bằng $-2$.
| $m=-4$ | |
| $m=5$ | |
| $m=1$ | |
| $m=4$ |
