Gọi $(d)$ là tiếp tuyến của đồ thị hàm số $y=f(x)=-x^3+x$ tại điểm $M(1;0)$. Tìm hệ số góc của $(d)$.
| $-2$ | |
| $2$ | |
| $1$ | |
| $0$ |
Đạo hàm của hàm số $y=\sqrt{x^2+1}$ là
| $y'=\dfrac{x}{2\sqrt{x^2+1}}$ | |
| $y'=\dfrac{1}{\sqrt{x^2+1}}$ | |
| $y'=\dfrac{x^2+1}{2\sqrt{x^2+1}}$ | |
| $y'=\dfrac{x}{\sqrt{x^2+1}}$ |
Tính đạo hàm của hàm số $y=\dfrac{2x-3}{x+4}$.
| $y’=\dfrac{5}{ (x+4)^2}$ | |
| $y'=\dfrac{11}{x+4}$ | |
| $y'=\dfrac{-11}{(x+4)^2}$ | |
| $y'=\dfrac{11}{(x+4)^2}$ |
Đạo hàm của hàm số $y=\left(3x-1\right)\cos x$ là
| $y'=3\cos x$ | |
| $y'=-\left(3x-1\right)\sin x$ | |
| $y'=3\cos x+(3x-1)\sin x$ | |
| $y'=3\cos x-(3x-1)\sin x$ |
Gọi $M(a;b)$ là điểm thuộc đồ thị hàm số $y=f(x)=x^3-3x^2+2$ $(\mathscr{C})$ sao cho tiếp tuyến của $(\mathscr{C})$ tại điểm $M$ có hệ số góc nhỏ nhất. Tính $a+b$.
| $-3$ | |
| $0$ | |
| $1$ | |
| $2$ |
Cho hàm số $f(x)=x^3-3x^2-9x-5$. Phương trình $f'(x)=0$ có nghiệm là
| $\{1;2\}$ | |
| $\{-1;2\}$ | |
| $\{-1;3\}$ | |
| $\{0;4\}$ |
Cho hàm số $y=f(x)=x^3-5x^2+2$ có đồ thị $(\mathscr{C})$. Có bao nhiêu tiếp tuyến của $(\mathscr{C})$ đi qua điểm $A(0;2)$?
| $1$ | |
| $4$ | |
| $3$ | |
| $2$ |
Cho hàm số $y=f(x)=x^3-3x^2+12$. Tìm $x$ để $f'(x)< 0$.
| $x\in(-2;0)$ | |
| $x\in(-\infty;-2)\cup(0;+\infty)$ | |
| $x\in(0;2)$ | |
| $x\in(-\infty;0)\cup(2;+\infty)$ |
Với mọi $x\neq0$ hàm số $g(x)=3x^2+\dfrac{1}{x^2}+3$ là đạo hàm của hàm số nào?
| $f(x)=x^3+\dfrac{1}{x}+3x+2$ | |
| $f(x)=x^3+\dfrac{1}{2x}+3x$ | |
| $f(x)=x^3-\dfrac{1}{x}+3x+1$ | |
| $f(x)=3x^3-\dfrac{1}{x}+3x$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=x^{2}+10x$, $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=f\left(x^4-8x^2+m\right)$ có đúng $9$ điểm cực trị?
| $16$ | |
| $9$ | |
| $15$ | |
| $10$ |
Cho hàm số $f(x)=3x^4+ax^3+bx^2+cx+d$ $(a,\,b,\,c,\,d\in\mathbb{R})$ có ba điểm cực trị là $-2,\,-1$ và $1$. Gọi $y=g(x)$ là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số $y=f(x)$. Diện tích hình phẳng giới hạn bởi hai đường $y=f(x)$ và $y=g(x)$ bằng
| $\dfrac{500}{81}$ | |
| $\dfrac{36}{5}$ | |
| $\dfrac{2932}{405}$ | |
| $\dfrac{2948}{405}$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=12x^2+2$, $\forall x\in\mathbb{R}$ và $f(1)=3$. Biết $F(x)$ là nguyên hàm của $f(x)$ thỏa mãn $F(0)=2$, khi đó $F(1)$ bằng
| $-3$ | |
| $1$ | |
| $2$ | |
| $7$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Số nghiệm thực phân biệt của phương trình $f'\left(f(x)\right)=0$ là
| $3$ | |
| $4$ | |
| $5$ | |
| $6$ |
Nếu $\displaystyle\displaystyle\int\limits_{1}^{3}f(x)\mathrm{\,d}x=2$ thì $\displaystyle\displaystyle\int\limits_{1}^{3}[f(x)+2x]\mathrm{\,d}x$ bằng
| $20$ | |
| $10$ | |
| $18$ | |
| $12$ |
Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
| $y=-x^3-x$ | |
| $y=-x^4-x^2$ | |
| $y=-x^3+x$ | |
| $y=\dfrac{x+2}{x-1}$ |
Trên đoạn $[1;5]$, hàm số $y=x+\dfrac{4}{x}$ đạt giá trị nhỏ nhất tại điểm
| $x=5$ | |
| $x=2$ | |
| $x=1$ | |
| $x=4$ |
Cho hàm số $y=ax^4+bx^2+c$ ($a,\,b,\,c\in\mathbb{R})$ có đồ thị là đường cong trong hình bên.
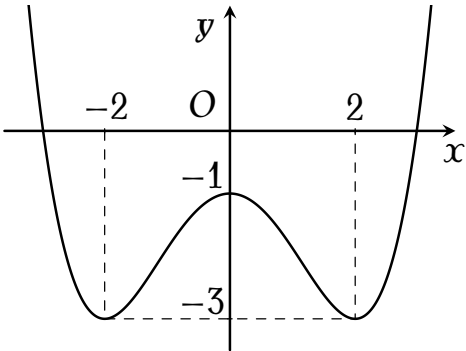
Giá trị cực đại của hàm số đã cho bằng
| $0$ | |
| $-1$ | |
| $-3$ | |
| $2$ |
Cho hàm số $f(x)=1+\sin x$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x-\cos x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x+\sin x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x+\cos x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\cos x+C$ |
Nếu $\displaystyle\displaystyle\int\limits_{2}^{5}f(x)\mathrm{\,d}x=2$ thì $\displaystyle\displaystyle\int\limits_{2}^{5}3f(x)\mathrm{\,d}x$ bằng
| $6$ | |
| $3$ | |
| $18$ | |
| $2$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
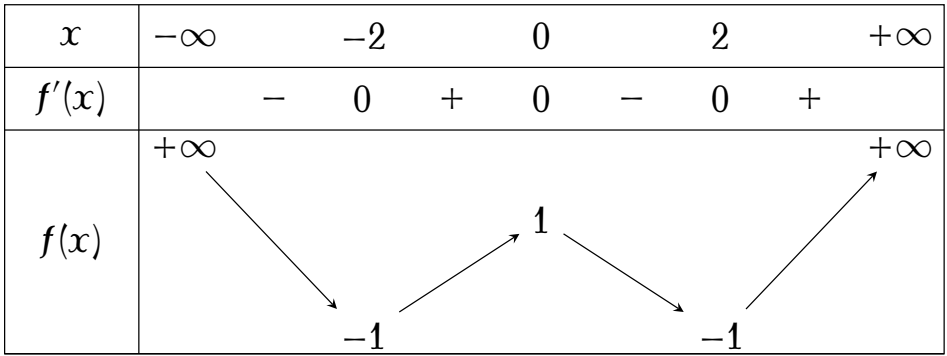
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
| $(0;+\infty)$ | |
| $(-\infty;-2)$ | |
| $(0;2)$ | |
| $(-2;0)$ |
