Một ô tô đang chạy với tốc độ \(36\) km/h thì người lái xe đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v(t)=-5t+10\) m/s, trong đó \(t\) là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

	\(10\) m
	\(20\) m
	\(2\) m
	\(0,2\) m

Một du khách vào trường đua ngựa đặt cược, lần đầu đặt \(20000\) đồng, mỗi lần sau tiền đặt cược gấp đôi lần trước đó. Người này thua \(9\) lần liên tiếp và thắng ở lần thứ \(10\). Hỏi du khách trên thắng hay thua bao nhiêu?

	Hòa vốn
	Thua \(20000\) đồng
	Thắng \(20000\) đồng
	Thua \(40000\) đồng

Người ta thiết kế một tòa tháp gồm \(11\) tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới, còn diện tích bề mặt trên của tầng một bằng nửa diện tích của đế tháp. Biết rằng diện tích đế tháp là \(12.288\text{ m}^2\), tính diện tích mặt trên của tầng trên cùng.

	\(6\text{ m}^2\)
	\(8\text{ m}^2\)
	\(10\text{ m}^2\)
	\(12\text{ m}^2\)

Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng đến để khoan giếng nước. Giá của mét khoan đầu tiên là \(80.000\) đồng, kể từ mét khoan thứ hai trở đi, giá của mỗi mét khoan tăng thêm \(5.000\) đồng so với giá của mét khoan trước đó. Biết rằng cần phải khoan sâu xuống \(50\) mét mới có nước. Vậy phải trả bao nhiêu tiền để khoan cái giếng đó?

	\(5.250.000\) đồng
	\(10.125.000\) đồng
	\(4.000.000\) đồng
	\(4.245.000\) đồng

Trên một bàn cờ có \(n\) ô vuông, người ta đặt \(7\) hạt dẻ vào ô đầu tiên. Mỗi ô tiếp theo, người ta đặt vào số hạt dẻ nhiều hơn \(5\) hạt so với ô trước đó. Biết rằng để đặt hết số ô trên bàn cờ, người ta phải sử dụng \(25450\) hạt dẻ. Hỏi bàn cờ đó có bao nhiêu ô vuông?

	\(98\)
	\(100\)
	\(102\)
	\(104\)

Một ô tô đang chạy với vận tốc \(54\) km/h thì tăng tốc chuyển động nhanh dần đều với gia tốc \(a(t)=3t-8\) (m/s\(^2\)) trong đó \(t\) là khoảng thời gian tính bằng giây. Quãng đường mà ô tô đi được sau \(10\) s kể từ lúc tăng tốc là

	\(540\) m
	\(150\) m
	\(250\) m
	\(246\) m

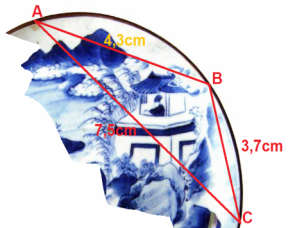
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy \(3\) điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (\(AB=4,3\) cm; \(BC=3,7\) cm; \(CA=7,5\) cm). Bán kính của chiếc đĩa này bằng

	\(6,01\)
	\(5,73\)
	\(5,85\)
	\(4,57\)

Tiền thưởng (triệu đồng) của nhân viên trong một công ty được cho ở bảng dưới đây:

Chênh lệch tiền thưởng (làm tròn đến hàng nghìn) trong bảng này là

	\(3.725.000\) đồng
	\(3.770.000\) đồng
	\(1.349.000\) đồng
	\(1.162.000\) đồng

Tiền thưởng (triệu đồng) của nhân viên trong một công ty được cho ở bảng dưới đây:

Tìm phương sai?

	\(3,725\)
	\(14,21\)
	\(1,35\)
	\(1,16\)

Tiền thưởng (triệu đồng) của nhân viên trong một công ty được cho ở bảng dưới đây:

Tiền thưởng trung bình (làm tròn đến hàng nghìn) là

	\(3.745.000\) đồng
	\(3.725.000\) đồng
	\(3.715.000\) đồng
	\(3.625.000\) đồng

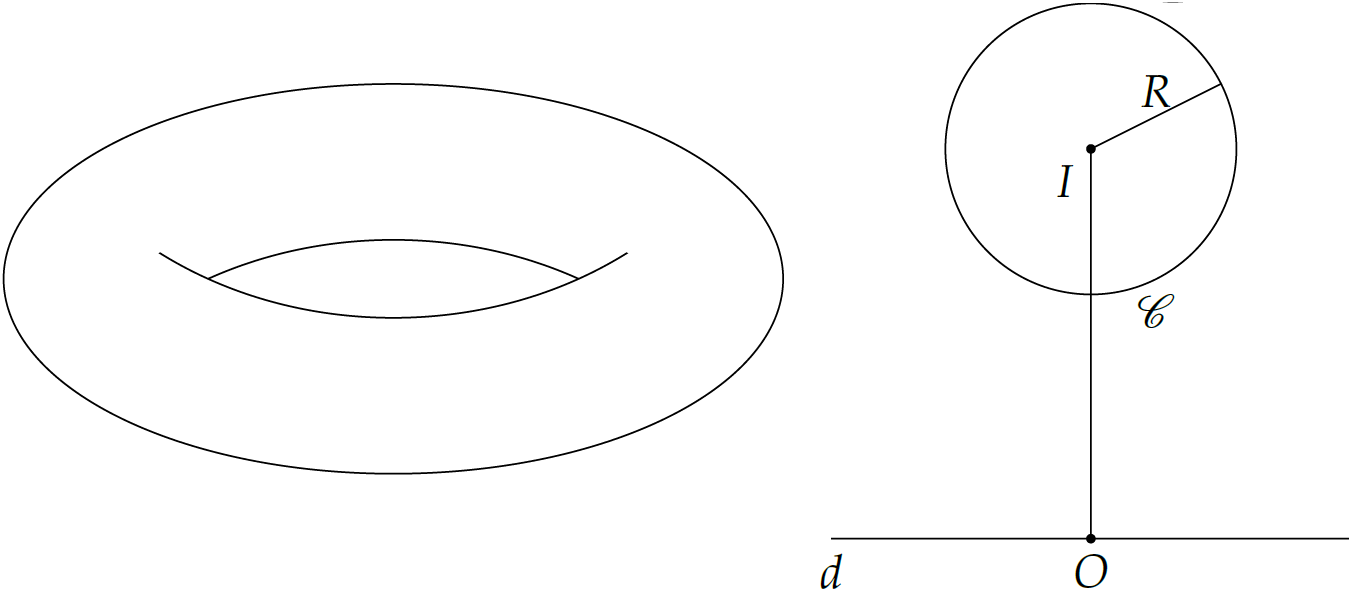
Người ta làm một chiếc phao bơi như hình vẽ (với bề mặt có được bằng cách quay đường tròn \(\mathscr{C}\) quanh trục \(d\)). Biết rằng \(OI=30\)cm, \(R=5\)cm. Tính thể tích \(V\) của chiếc phao.

	\(V=1500\pi^2\text{cm}^3\)
	\(V=9000\pi^2\text{cm}^3\)
	\(V=1500\pi\text{cm}^3\)
	\(V=9000\pi\text{cm}^3\)

Một ô tô đang đi với vận tốc lớn hơn \(72\)km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là \(72\)km/h, vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc \(v(t)=30-2t\) (m/s), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ \(72\)km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét?

	\(100\)m
	\(150\)m
	\(175\)m
	\(125\)m

Để dự báo dân số của một quốc gia, người ta sử dụng công thức \(S=A\mathrm{e}^{nr}\); trong đó \(A\) là dân số của năm lấy làm mốc tính, \(S\) là dân số sau \(n\) năm, \(r\) là tỉ lệ tăng dân số hàng năm. Năm \(2017\), dân số Việt Nam là \(93.671.600\) người (Tổng cục Thống kê, Niên giám Thống kê năm \(2017\), Nhà xuất bản Thống kê, Tr. \(79\)). Giả sử tỉ lệ tăng dân số hàng năm không đổi là \(0,81\%\) dự báo dân số Việt Nam năm \(2035\) là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)?

	\(109.256.100\)
	\(108.374.700\)
	\(107.500.500\)
	\(108.311.100\)

Từ một nhóm học sinh gồm \(6\) nam và \(8\) nữ, có bao nhiêu cách chọn ra một học sinh?

	\(14\)
	\(48\)
	\(6\)
	\(8\)

Lớp \(10A4\) có \(7\) học sinh giỏi Toán, \(5\) học sinh giỏi Lý, \(6\) học sinh giỏi Hóa, \(3\) học sinh giỏi cả Toán và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(2\) học sinh giỏi cả Lý và Hóa, \(1\) học sinh giỏi cả Toán, Lý, Hóa. Tìm số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A4.

	\(9\)
	\(10\)
	\(18\)
	\(28\)

Lớp \(10A4\) có \(7\) học sinh giỏi Toán, \(5\) học sinh giỏi Lý, \(6\) học sinh giỏi Hóa, \(3\) học sinh giỏi cả Toán và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(2\) học sinh giỏi cả Lý và Hóa, \(1\) học sinh giỏi cả Toán, Lý, Hóa. Tìm số học sinh giỏi đúng hai môn (Toán, Lý, Hóa) của lớp 10A4.

	\(6\)
	\(7\)
	\(9\)
	\(10\)

Một lớp học có \(50\) học sinh, trong đó có \(30\) em biết chơi bóng chuyền, \(25\) em biết chơi bóng đá, \(10\) em biết chơi cả bóng đá và bóng chuyền. Hỏi có bao nhiêu em không biết chơi cả bóng đá và bóng chuyền?

	\(15\)
	\(5\)
	\(20\)
	\(45\)

Lớp 10A4 có \(45\) học sinh, trong đó có \(17\) bạn giỏi Văn, \(25\) bạn giỏi Toán và \(13\) bạn không giỏi cả Văn và Toán. Hỏi lớp 10A4 có bao nhiêu bạn giỏi cả Văn và Toán?

	\(42\)
	\(32\)
	\(17\)
	\(10\)

Một người gửi tiết kiệm với lãi suất \(5\)%/năm và lãi hàng năm được nhập vào vốn. Sau ít nhất bao nhiêu năm thì người đó nhận được số tiền lớn hơn \(150\)% số tiền gửi ban đầu?

	\(8\) năm
	\(10\) năm
	\(9\) năm
	\(11\) năm

Một người gửi số tiền \(50\) triệu đồng vào một ngân hàng với lãi suất \(8,4\%\)/năm. Cứ mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Người đó sẽ lĩnh được số tiền cả vốn lẫn lãi là \(80\) triệu sau \(n\) năm. Hỏi nếu trong khoảng thời gian này người đó không rút tiền và lãi suất không thay đổi thì \(n\) gần nhất với số nào sau đây?

	\(4\)
	\(5\)
	\(6\)
	\(7\)