Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,b,c\in\mathbb{R}$) có đồ thị như hình bên.
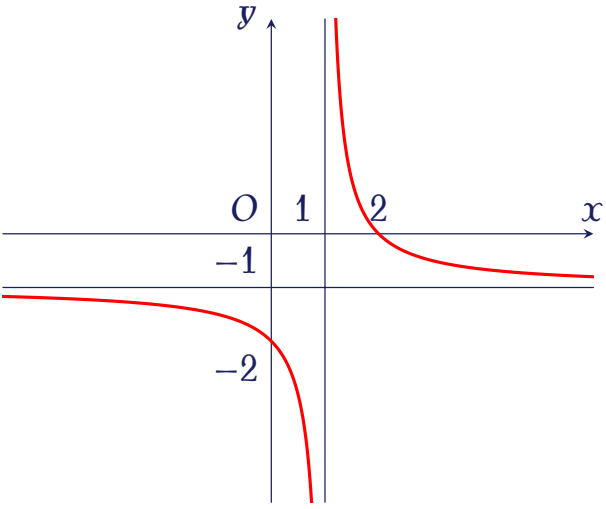
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Tìm giá trị nhỏ nhất của hàm số $y=x+\dfrac{3}{x}-4$ trên đoạn $[1;5]$.
| $\dfrac{8}{5}$ | |
| $4-2\sqrt{3}$ | |
| $0$ | |
| $2\sqrt{3}-4$ |
Đồ thị của hàm số nào dưới đây cắt trục hoành tại $3$ điểm phân biệt?
| $y=x^3-3x+3$ | |
| $y=x^3+3x+1$ | |
| $y=-x^3+3x+5$ | |
| $y=x^3-3x+1$ |
Tìm giá trị nhỏ nhất của hàm số $y=2\sqrt{x+2}$ trên đoạn $[-1;3]$.
| $1$ | |
| $2$ | |
| $4$ | |
| $-1$ |
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y=\big|x^4-2mx^2+64x\big|$ có đúng ba điểm cực trị?
| $5$ | |
| $6$ | |
| $12$ | |
| $11$ |
Cho hàm số $f(x)=(m-1)x^4-2mx^2+1$ với $m$ là tham số thực. Nếu $\min\limits_{[0;3]}f(x)=f(2)$ thì $\max\limits_{[0;3]}f(x)$ bằng
| $-\dfrac{13}{3}$ | |
| $4$ | |
| $-\dfrac{14}{3}$ | |
| $1$ |
Hàm số nào dưới đây đồng biến trên $\mathbb{R}$?
| $y=x^4-x^2$ | |
| $y=x^3-x$ | |
| $y=\dfrac{x-1}{x+2}$ | |
| $y=x^3+x$ |
Giá trị lớn nhất của hàm số $f(x)=x^3-3x^2-9x+10$ trên đoạn $[-2;2]$ bằng
| $-12$ | |
| $10$ | |
| $15$ | |
| $-1$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị như đường cong trong hình bên.
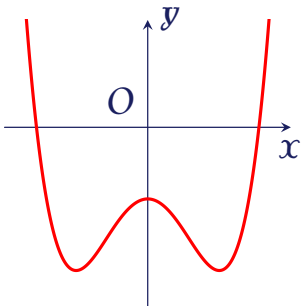
Số điểm cực trị của hàm số đã cho là
| $2$ | |
| $3$ | |
| $1$ | |
| $0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
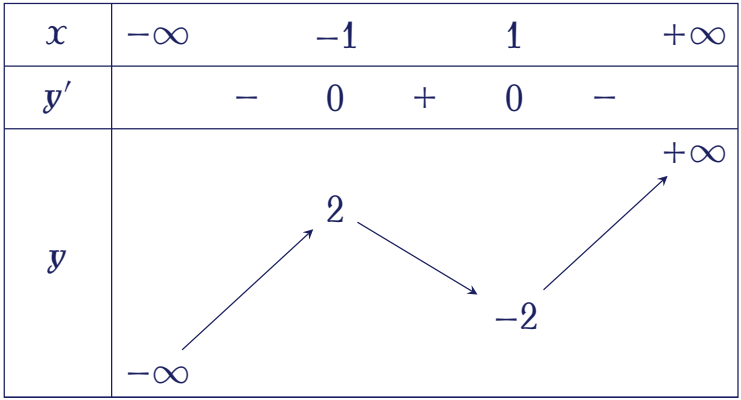
Điểm cực tiểu của hàm số đã cho là
| $x=-2$ | |
| $x=2$ | |
| $x=-1$ | |
| $x=1$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
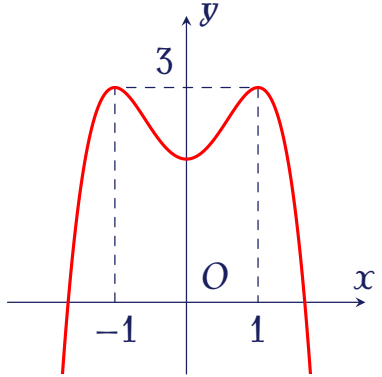
Số nghiệm thực của phương trình $f(x)=1$ là
| $1$ | |
| $2$ | |
| $4$ | |
| $3$ |
Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
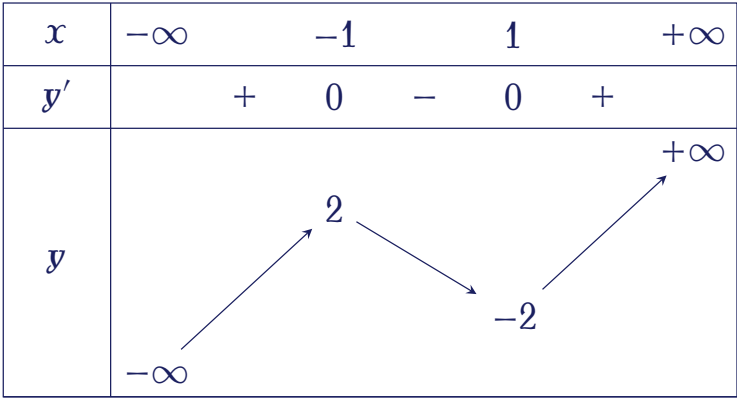
| $y=x^4-2x^2$ | |
| $y=-x^3+3x$ | |
| $y=-x^4+2x^2$ | |
| $y=x^3-3x$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x-1}{2x+4}$ là đường thẳng có phương trình
| $x=-2$ | |
| $x=1$ | |
| $y=1$ | |
| $y=-2$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
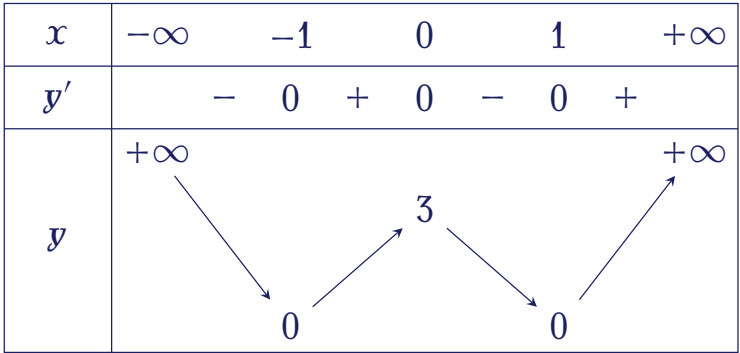
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(1;+\infty)$ | |
| $(0;1)$ | |
| $(-1;0)$ | |
| $(0;+\infty)$ |
Tìm các điểm cực trị hàm số $f(x)=x^3-3x+1$.
Có bao nhiêu giá trị của $m$ để đồ thị của hàm số $y=\dfrac{x}{1-x}$ cắt đường thẳng $y=x-m$ tại hai điểm phân biệt $A,\,B$ sao cho góc giữa hai đường thẳng $OA$ và $OB$ bằng $60^\circ$ ($O$ là gốc tọa độ)?
| $2$ | |
| $1$ | |
| $3$ | |
| $0$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{-1\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên.
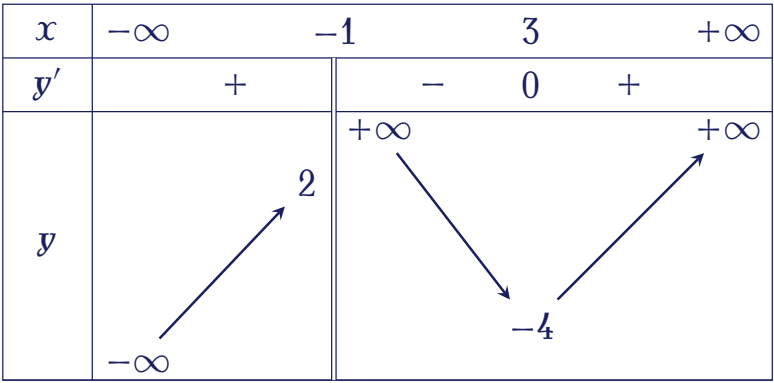
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho phương trình $f(x)=m$ có đúng ba nghiệm thực phân biệt.
| $(-4;2)$ | |
| $[-4;2)$ | |
| $(-4;2]$ | |
| $(-\infty;2]$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị như hình vẽ bên.
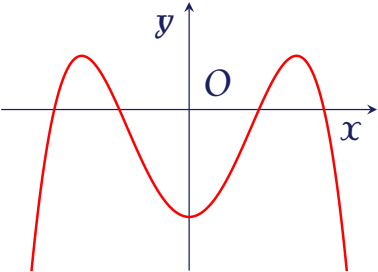
Mệnh đề nào dưới đây đúng?
| $a>0,\,b< 0,\,c< 0$ | |
| $a< 0,\,b< 0,\,c< 0$ | |
| $a< 0,\,b>0,\,c< 0$ | |
| $a>0,\,b< 0,\,c>0$ |
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
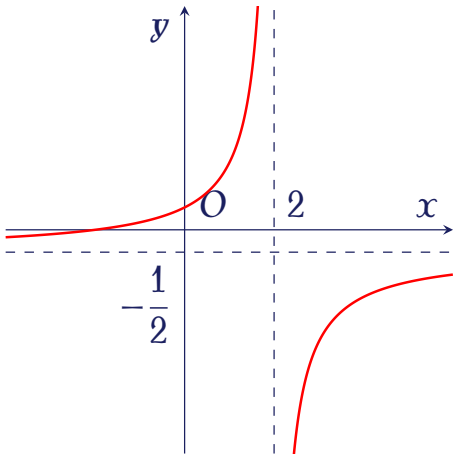
| $y=\dfrac{x+2}{-2x+4}$ | |
| $y=\dfrac{-x+1}{x-2}$ | |
| $y=\dfrac{2x-3}{x+2}$ | |
| $y=\dfrac{-x+3}{2x-4}$ |
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
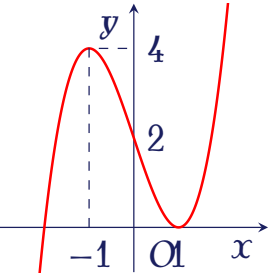
| $y=-x^3+3x+2$ | |
| $y=x^3-2x+2$ | |
| $y=x^3-3x+2$ | |
| $y=x^3+3x+2$ |
