Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?
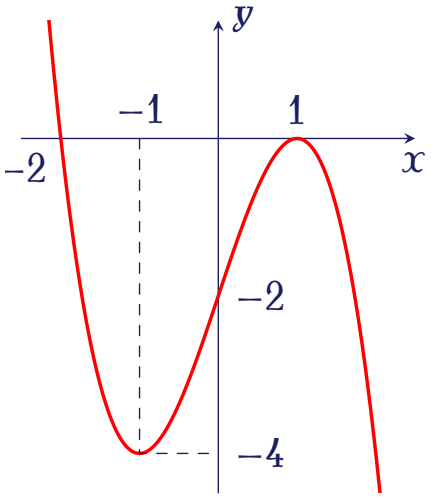
| $y=-x^3+3x-2$ | |
| $y=x^3-3x+2$ | |
| $y=x^4-3x^2-2$ | |
| $y=x^4-3x^2+2$ |
Cho hàm số $y=\dfrac{2x+1}{-x+1}$. Khẳng định nào sau đây đúng?
| Hàm số nghịch biến trên $\mathbb{R}\setminus\{1\}$ | |
| Hàm số đồng biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ | |
| Hàm số đồng biến trên $\mathbb{R}\setminus\{1\}$ | |
| Hàm số nghịch biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ |
Đồ thị hàm số nào sau đây có tiệm cận ngang?
| $y=\dfrac{1-x^2}{x}$ | |
| $y=\dfrac{\sqrt{x^2-1}}{x}$ | |
| $y=\dfrac{x^2-1}{x}$ | |
| $y=\dfrac{\sqrt{1-x^2}}{x}$ |
Bảng biến thiên trong hình bên là của hàm số nào trong các hàm số đã cho dưới đây?
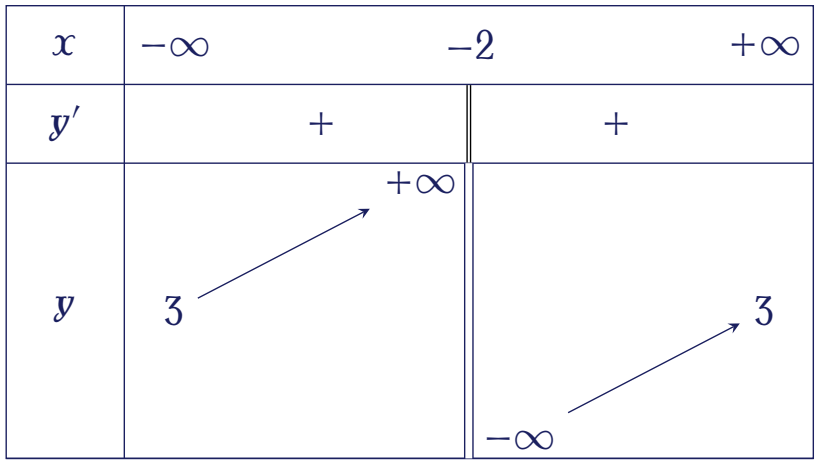
| $y=\dfrac{3-x}{x+2}$ | |
| $y=\dfrac{3x+8}{x+2}$ | |
| $y=\dfrac{3x-3}{x+2}$ | |
| $y=\dfrac{3-3x}{x+2}$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x-3}$ là đường thẳng có phương trình
| $x=\dfrac{1}{2}$ | |
| $x=\dfrac{1}{3}$ | |
| $x=2$ | |
| $x=3$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Phát biểu nào sau đây đúng?
| Hàm số $y=f(x)$ đạt cực trị tại $x_0$ khi và chỉ khi $x_0$ là nghiệm của đạo hàm | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)>0$ thì hàm số đạt cực đại tại $x_0$ | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)=0$ thì $x_0$ không phải là cực trị của hàm số $y=f(x)$ đã cho | |
| Nếu $f'(x)$ đổi dấu khi $x$ qua điểm $x_0$ và $y=f(x)$ liên tục tại $x_0$ thì hàm số $y=f(x)$ đạt cực trị tại điểm $x_0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên sau:
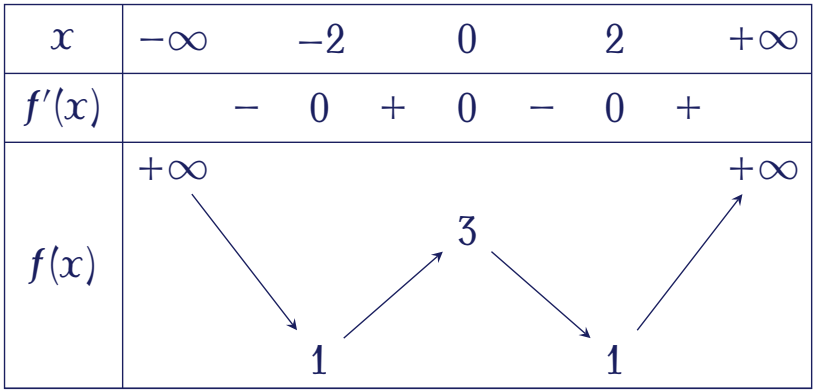
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
| $(1;3)$ | |
| $(-\infty;-2)$ | |
| $(0;+\infty)$ | |
| $(-2;0)$ |
Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3}x^3-mx^2+9x-1$ đồng biến trên $\mathbb{R}$?
| $8$ | |
| $9$ | |
| $7$ | |
| $6$ |
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=x^4-2mx^2+2m^4-m$ có $3$ điểm cực trị đều nằm trên các trục tọa độ.
| $\{0;1\}$ | |
| $\{1\}$ | |
| $\{-1;1\}$ | |
| $\{0\}$ |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ dưới đây:
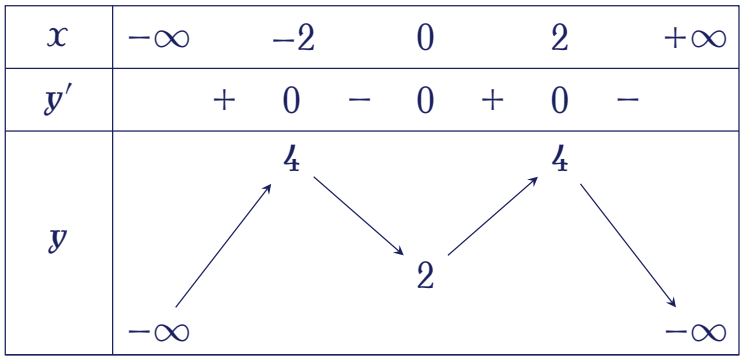
Số nghiệm của phương trình $f^2(x)-4f(x)+3=0$ là
| $5$ | |
| $3$ | |
| $6$ | |
| $4$ |
Gọi $x_1,\,x_2$ là các điểm cực trị của hàm số $y=x^3-2x^2-7x+1$. Tính $x_1^2+x_2^2$.
| $\dfrac{44}{9}$ | |
| $\dfrac{16}{3}$ | |
| $\dfrac{28}{3}$ | |
| $\dfrac{58}{9}$ |
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là
| $4$ | |
| $3$ | |
| $2$ | |
| $1$ |
Đồ thị của hàm số nào dưới đây có đúng một điểm cực trị?
| $y=x^3-2x^2-1$ | |
| $y=-x^4+2x^2-1$ | |
| $y=x^4-2x^2-1$ | |
| $y=x^4+2x^2+1$ |
Cho hàm số $f(x)$ có bảng biến thiên như sau:
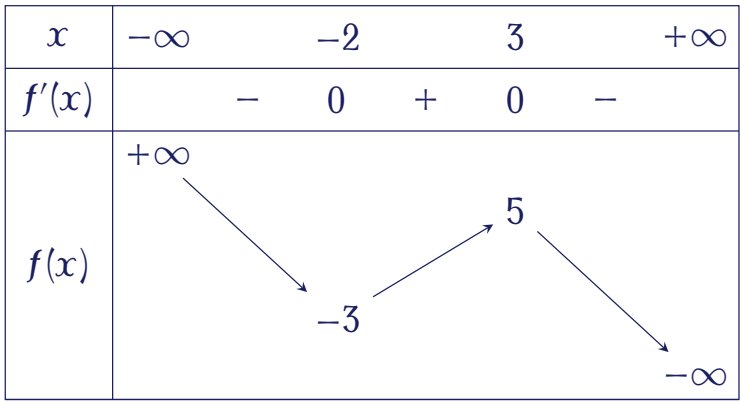
Hàm số đã cho đạt cực đại tại
| $x=-2$ | |
| $x=3$ | |
| $x=5$ | |
| $x=-3$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Cho hàm số $f(x)$ có bảng xét dấu của đạo hàm như sau:
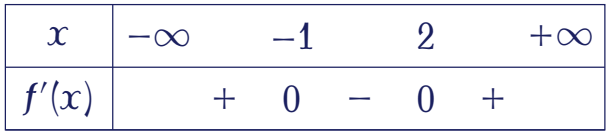
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
| $(-\infty;2)$ | |
| $(-\infty;-1)$ | |
| $(1;2)$ | |
| $(-1;+\infty)$ |
Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
| $y=3x^3-x$ | |
| $y=-2x^4-x$ | |
| $y=-2x^3+3$ | |
| $y=-x^4+2$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
