Một người gửi tiết kiệm số tiền \(80\) triệu đồng với lãi suất \(6,9\%\)/năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc. Hỏi sau đúng \(5\) năm người đó rút được cả gốc và lãi số tiền gần với con số nào sau đây?
| \(105,370\) triệu đồng | |
| \(107,667\) triệu đồng | |
| \(111,680\) triệu đồng | |
| \(116,570\) triệu đồng |
Việt Nam là quốc gia nằm ở phía Đông bán đảo Đông Dương thuộc khu vực Đông Nam Á. Với dân số ước tính \(93,7\) triệu dân vào đầu năm 2018, Việt Nam là quốc gia đông dân thứ \(15\) trên thế giới và là quốc gia đông dân thứ \(8\) ở châu Á, tỉ lệ tăng dân số hàng năm \(1,2\%\). Giả sử rằng tỉ lệ tăng dân số từ năm 2018 đến năm 2030 không thay đổi thì dân số nước ta đầu năm 2030 khoảng bao nhiêu?
| \(118,12\) triệu dân | |
| \(106,12\) triệu dân | |
| \(128,12\) triệu dân | |
| \(108,12\) triệu dân |
Để đầu tư dự án trồng rau sạch theo công nghệ mới, bác Năm đã làm hợp đồng xin vay vốn ngân hàng số tiền \(100\) triệu đồng với lãi suất \(x\%\) mỗi năm. Điều kiện kèm theo của hợp đồng là số tiền lãi năm trước sẽ được tính làm vốn để sinh lãi cho năm sau. Sau hai năm thành công với dự án rau sạch của mình, bác Năm đã thanh toán hợp đồng ngân hàng số tiền làm tròn là \(129.512.000\) đồng. Khẳng định nào sau đây đúng?
| \(x=13\) | |
| \(x=15\) | |
| \(x=12\) | |
| \(x=14\) |
Một khu rừng có trữ lượng gỗ \(4\cdot10^5\) mét khối. Biết tốc độ sinh trưởng của các cây trong rừng đó là \(4\%\) mỗi năm. Hỏi sau \(10\) năm khu rừng đó có số mét khối gỗ gần nhất với số nào sau đây?
| \(5,9\cdot10^5\) | |
| \(5,92\cdot10^5\) | |
| \(5,93\cdot10^5\) | |
| \(5,94\cdot10^5\) |
Một người gửi tiết kiệm số tiền \(80.000.000\) đồng với lãi suất \(6,9\%\)/năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng \(5\) năm người đó rút được cả gốc lẫn lãi với số tiền gần với con số nào nhất sau đây?
| \(116.570.000\) đồng | |
| \(107.667.000\) đồng | |
| \(105.370.000\) đồng | |
| \(111.680.000\) đồng |
Ông Bình gửi số tiền \(58\) triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong \(9\) tháng thì lãnh được \(61.758.000\) đồng. Hỏi lãi suất ngân hàng mỗi tháng là bao nhiêu, biết rằng lãi suất không thay đổi trong suốt thời gian gửi?
| \(0,8\%\) | |
| \(0,6\%\) | |
| \(0,7\%\) | |
| \(0,5\%\) |
Cho các hàm số \(y=\log_ax\), \(y=b^x\), \(y=c^x\) có đồ thị như hình vẽ.
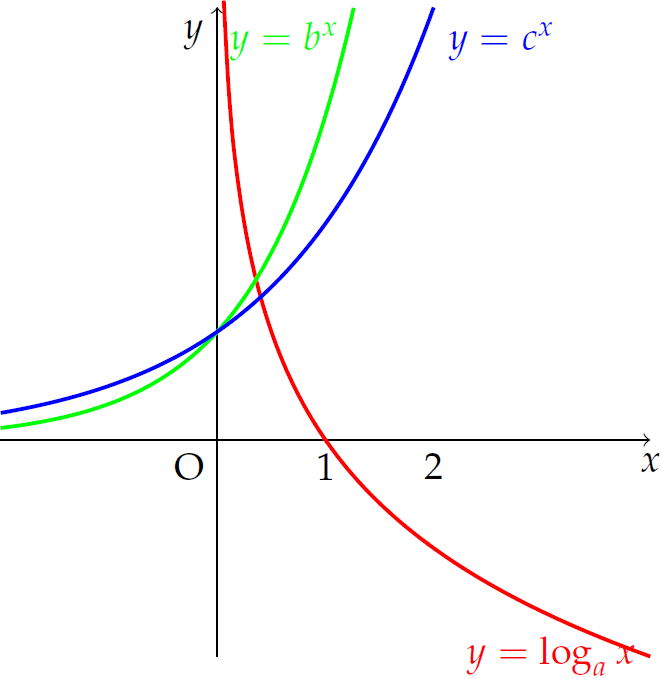
Mệnh đề nào dưới đây là đúng?
| \(b>c>a\) | |
| \(a>b>c\) | |
| \(b>a>c\) | |
| \(c>b>a\) |
Hình vẽ bên biểu diễn đồ thị của hai hàm số \(y=a^x\) và \(y=\log_bx\) với \(a,\,b\) là các số thực dương và \(b\neq1\).
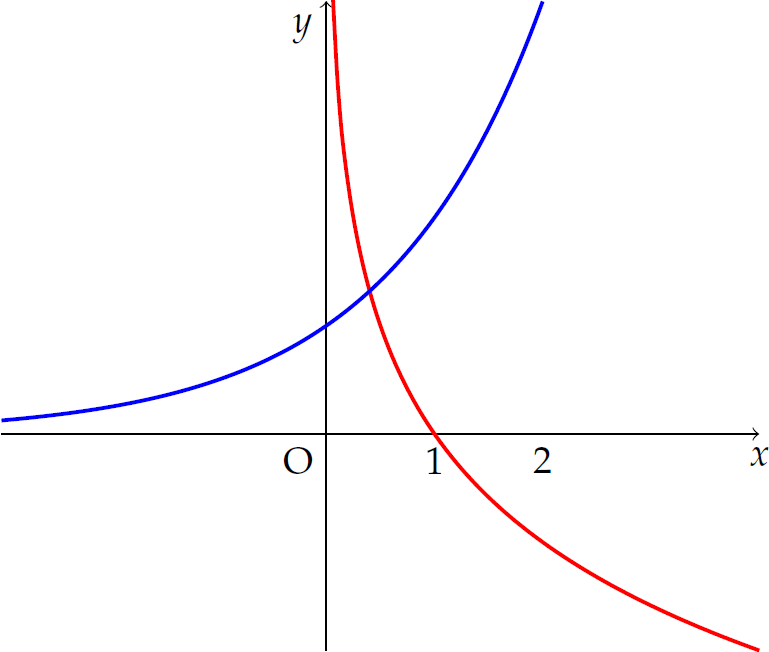
Mệnh đề nào dưới đây là đúng?
| \(\log_ab^2>0\) | |
| \(\log_ab<0\) | |
| \(\log_ab>0\) | |
| \(\log_ba>0\) |
Cho ba số thực dương \(a,\,b,\,c\) khác \(1\). Đồ thị hàm số \(y=a^x\), \(y=b^x\) và \(y=c^x\) được cho trong hình vẽ.
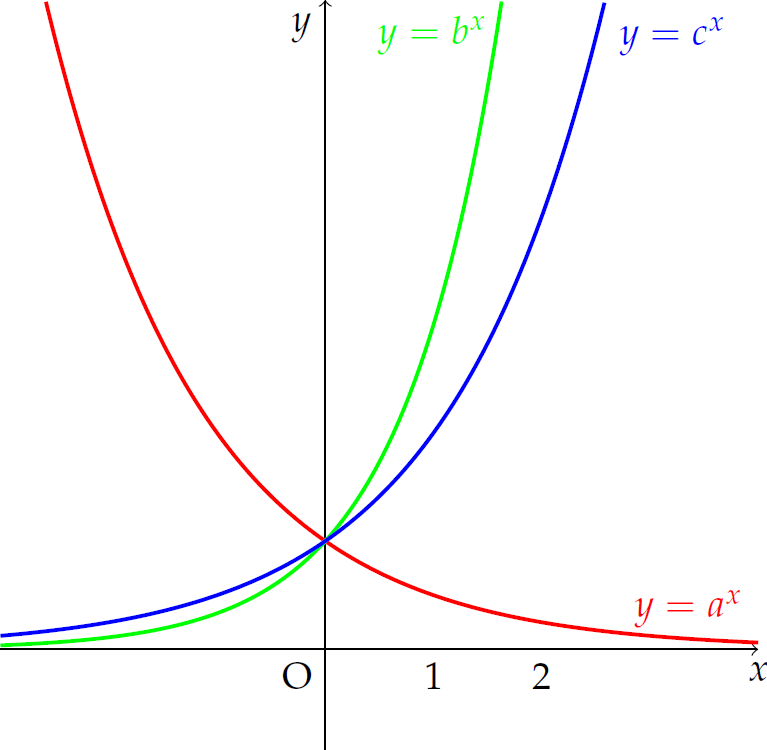
Mệnh đề nào dưới đây là đúng?
| \(a< b< c\) | |
| \(a< c< b\) | |
| \(b< c< a\) | |
| \(c< a< b\) |
Cho \(a,\,b,\,c\) dương và khác \(1\). Đồ thị hàm số \(y=\log_ax\), \(y=\log_bx\) và \(y=\log_cx\) được cho trong hình vẽ.
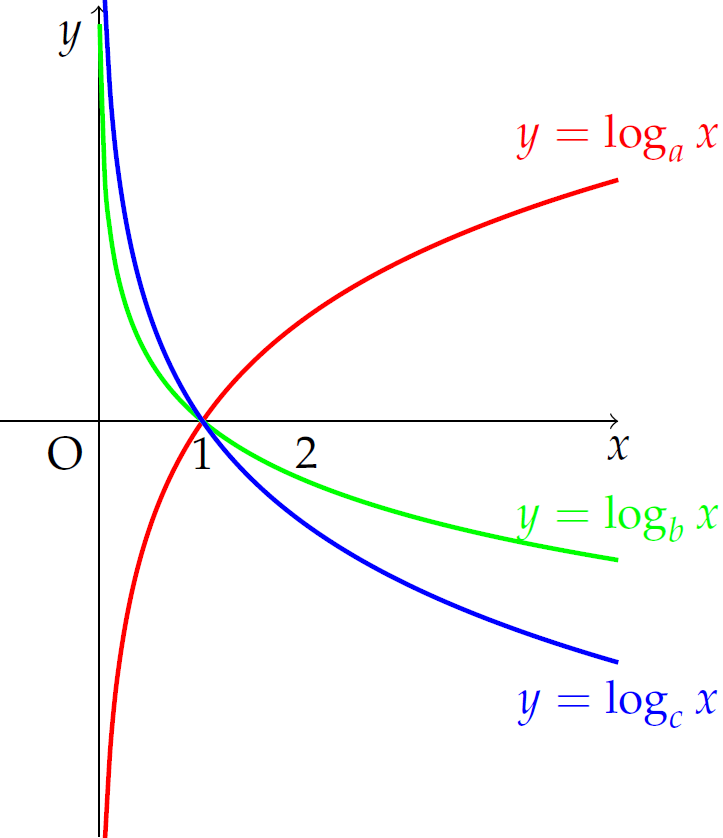
Khẳng định nào dưới đây là đúng?
| \(a>c>b\) | |
| \(b>c>a\) | |
| \(c>b>a\) | |
| \(a>b>c\) |
Số điểm cực trị của hàm số \(y=\mathrm{e}^x+x+1\) là
| \(0\) | |
| \(3\) | |
| \(2\) | |
| \(1\) |
Tìm các khoảng đồng biến của hàm số $$y=2^{x^2-6x+5}$$
| \((-\infty;3)\) | |
| \(\mathbb{R}\) | |
| \((3;+\infty)\) | |
| \((-\infty;1)\) và \((5;+\infty)\) |
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\mathbb{R}\)?
| \(y=\left(\dfrac{\pi}{3}\right)^x\) | |
| \(y=\log_{\tfrac{\pi}{4}}\left(2x^2+1\right)\) | |
| \(y=\left(\dfrac{2}{\mathrm{e}}\right)^x\) | |
| \(y=\log_{\tfrac{2}{3}}x\) |
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
| \(y=2019^x\) | |
| \(y=3^{-x}\) | |
| \(y=\left(\sqrt{\pi}\right)^x\) | |
| \(y=\mathrm{e}^x\) |
Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
| \(y=\log_2x\) | |
| \(y=\dfrac{x-1}{x+1}\) | |
| \(y=3^x\) | |
| \(y=x^4+2x^2+4\) |
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
| \(y=\left(\dfrac{\mathrm{e}}{2}\right)^{-2x}\) | |
| \(y=\left(\dfrac{3}{\mathrm{e}}\right)^x\) | |
| \(y=\left(\dfrac{1}{3}\right)^{-x}\) | |
| \(y=2019^x\) |
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
| \(y=\log_{\tfrac{\pi}{4}}x\) | |
| \(y=\log_\pi x\) | |
| \(y=\left(\dfrac{\sqrt{5}}{2}\right)^x\) | |
| \(y=2^x\) |
Cho hàm số \(y=\log_2x\). Khẳng định nào sau đây sai?
| Đồ thị hàm số nhận trục tung làm tiệm cận đứng | |
| Đồ thị hàm số cắt trục hoành tại điểm \(A(1;0)\) | |
| Đồ thị hàm số luôn nằm phía trên trục hoành | |
| Hàm số đồng biến trên khoảng \((0;+\infty)\) |
Cho hàm số \(y=\log_{2019}x\) có đồ thị \((\mathscr{C})\). Mệnh đề nào sau đây sai?
| \((\mathscr{C})\) có đúng một tiệm cận | |
| \((\mathscr{C})\) không có tiệm cận ngang | |
| \((\mathscr{C})\) đồng biến trên tập xác định | |
| \((\mathscr{C})\) không có tiệm cận đứng |
Đạo hàm của hàm số \(y=\log_3(x+1)-2\ln(x-1)+2x\) tại điểm \(x=2\) bằng
| \(\dfrac{1}{3}\) | |
| \(\dfrac{1}{3\ln3}+2\) | |
| \(\dfrac{1}{3\ln3}-1\) | |
| \(\dfrac{1}{3\ln3}\) |
