Cho hình hộp $ABCD.A'B'C'D'$. Chọn khẳng định đúng.
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{BB'}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{AC'}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{CD}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{AC}$ |
Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
Hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$. Hình chiếu vuông góc của $A'$ lên mặt phẳng $(ABC)$ là điểm $I$ thuộc cạnh $BC$. Khoảng cách từ $A$ tới mặt phẳng $(A'BC)$ bằng
| $\dfrac{2}{5}a$ | |
| $\dfrac{\sqrt{3}}{2}a$ | |
| $\dfrac{2a\sqrt{5}}{5}$ | |
| $\dfrac{a\sqrt{5}}{5}$ |
Cho hình lăng trụ có cạnh bên vuông góc với mặt đáy, khi đó các mặt bên của lăng trụ là hình gì?
| Hình chữ nhật | |
| Hình bình hành | |
| Hình thoi | |
| Hình vuông |
Trong không gian, cho tứ diện $ABCD$ có trọng tâm $S$. Gọi $G$ là trọng tâm tam giác $BCD$, $M$ và $N$ lần lượt là trung điểm của $AB$, $CD$. Mệnh đề nào sau đây là sai?
| $S$ là trung điểm đoạn $MN$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $S$ nằm trên đoạn $AG$ sao cho $SA=3SG$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ |
Trong không gian, cho tứ diện $ABCD$ có $M,\,N$ lần lượt là trung điểm của $AB,\,CD$. Chọn mệnh đề sai trong các mệnh đề sau:
| $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$ | |
| $\overrightarrow{NC}+\overrightarrow{NC}=\overrightarrow{0}$ | |
| $\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CM}$ | |
| $\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AM}$ |
Trong không gian, điểm $S$ là trọng tâm của tứ diện $ABCD$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}+\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=3\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{A0}$ |
Trong không gian, điểm $S$ là trọng tâm của tam giác $ABC$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AS}$ |
Cho tứ diện $ABCD$ có $G$ là trọng tâm tam giác $BCD$. Mệnh đề nào sau đây không đúng?
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}$ | |
| $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ | |
| $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}-3\overrightarrow{AG}=\overrightarrow{0}$ |
Cho 5 khẳng định sau về hình lăng trụ. Hỏi có bao nhiêu khẳng định đúng?
- Hình lăng trụ có tất cả các mặt bên đều là hình bình hành;
- Hình lăng trụ có 2 đáy là những đa giác bằng nhau và nằm trên 2 mặt phẳng song song;
- Hình lăng trụ có tất cả các cạnh bên song song và bằng nhau;
- Hình lăng trụ có 2 đáy đều là hình bình hành;
- Hình lăng trụ có tất cả các mặt bên đều là những hình chữ nhật.
| $4$ | |
| $5$ | |
| $3$ | |
| $2$ |
Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa 2 vectơ $\overrightarrow{AB},\,\overrightarrow{A'C'}$.
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=45^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=60^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=30^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=90^\circ$ |
Cho 2 vectơ $\overrightarrow{u}=\overrightarrow{AB}$, $\overrightarrow{v}=\overrightarrow{AC}$. Khi đó $\big(\overrightarrow{u},\overrightarrow{v}\big)$ bằng
| $\widehat{ABC}$ | |
| $90^\circ$ | |
| $\widehat{ACB}$ | |
| $\widehat{BAC}$ |
Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân tại $A$, $AB=AC=a$ và $SA=SB=SC=a$. Tính $\overrightarrow{AB}\cdot\overrightarrow{SC}$.
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2\sqrt{3}}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2\sqrt{3}}{2}$ |
Cho 2 vectơ $\overrightarrow{u},\,\overrightarrow{v}$ có $\big|\overrightarrow{u}\big|=2$, $\big|\overrightarrow{v}\big|=5$ và $\big(\overrightarrow{u},\overrightarrow{v}\big)=30^\circ$. Tính $\overrightarrow{u}\cdot\overrightarrow{v}$.
| $\overrightarrow{u}\cdot\overrightarrow{v}=5\sqrt{2}$ | |
| $\overrightarrow{u}\cdot\overrightarrow{v}=5$ | |
| $\overrightarrow{u}\cdot\overrightarrow{v}=10$ | |
| $\overrightarrow{u}\cdot\overrightarrow{v}=5\sqrt{3}$ |
Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa 2 đường thẳng $AC$ và $B'C$.
| $30^\circ$ | |
| $45^\circ$ | |
| $60^\circ$ | |
| $90^\circ$ |
Cho hình hộp $ABCD.A'B'C'D'$ (tham khảo hình vẽ).
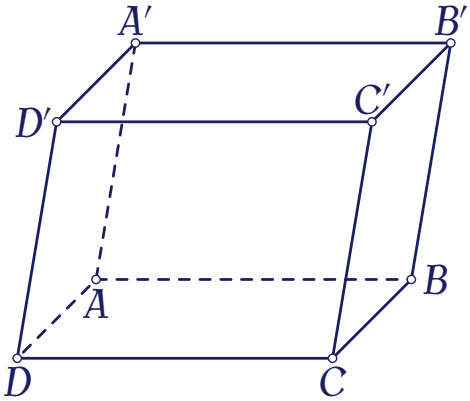
Khẳng định nào sau đây là đúng?
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BA'}$ | |
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{B'D}$ | |
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BD'}$ | |
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BC'}$ |
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=a$, $BC=2a$ và $AA'=3a$ (tham khảo hình bên).
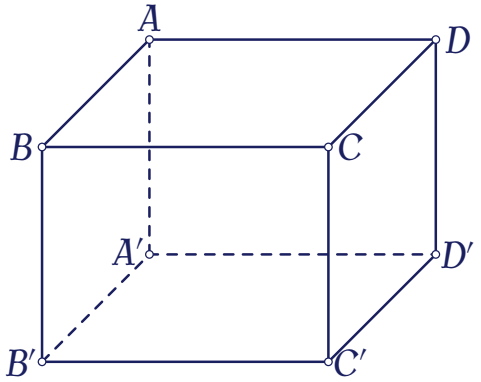
Khoảng cách giữa hai đường thẳng $BD$ và $A'C'$ bằng
| $a$ | |
| $a\sqrt{2}$ | |
| $2a$ | |
| $3a$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AC=2$, $AB=\sqrt{3}$ và $AA'=1$ (tham khảo hình bên).
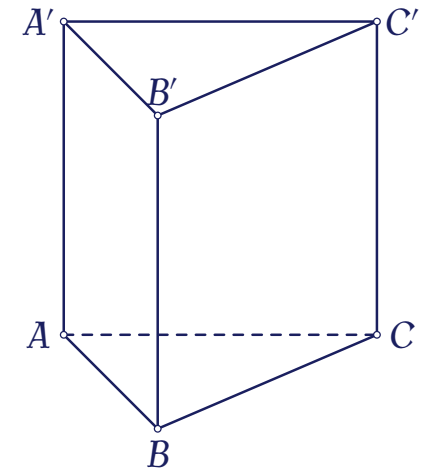
Góc giữa hai mặt phẳng $(ABC')$ và $(ABC)$ bằng
| $30^\circ$ | |
| $45^\circ$ | |
| $90^\circ$ | |
| $60^\circ$ |
Trong mặt phẳng $Oxy$, cho các điểm $A(1;3)$, $B(4;0)$, $C(2;-5)$. Tọa độ điểm $M$ thỏa mãn $\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{0}$ là
| $M\left(1;18\right)$ | |
| $M\left(-1;18\right)$ | |
| $M\left(1;-18\right)$ | |
| $M\left(-18;1\right)$ |
Trong không gian \(Oxyz\), cho \(A(1;-1;0)\), \(B(0;2;0)\) và \(C(2;1;3)\). Tọa độ điểm \(M\) thỏa mãn \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\) là
| \(M(3;2;-3)\) | |
| \(M(3;-2;3)\) | |
| \(M(3;-2;-3)\) | |
| \(M(3;2;3)\) |
