Trong không gian, cho tứ diện $ABCD$ có trọng tâm $S$. Gọi $G$ là trọng tâm tam giác $BCD$, $M$ và $N$ lần lượt là trung điểm của $AB$, $CD$. Mệnh đề nào sau đây là sai?
| $S$ là trung điểm đoạn $MN$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $S$ nằm trên đoạn $AG$ sao cho $SA=3SG$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ |
Trong không gian, cho tứ diện $ABCD$ có $M,\,N$ lần lượt là trung điểm của $AB,\,CD$. Chọn mệnh đề sai trong các mệnh đề sau:
| $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$ | |
| $\overrightarrow{NC}+\overrightarrow{NC}=\overrightarrow{0}$ | |
| $\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CM}$ | |
| $\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AM}$ |
Trong không gian, điểm $S$ là trọng tâm của tứ diện $ABCD$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}+\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=3\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{A0}$ |
Trong không gian, điểm $S$ là trọng tâm của tam giác $ABC$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AS}$ |
Cho tứ diện $ABCD$ có $G$ là trọng tâm tam giác $BCD$. Mệnh đề nào sau đây không đúng?
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}$ | |
| $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ | |
| $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}-3\overrightarrow{AG}=\overrightarrow{0}$ |
Cho hình hộp $ABCD.A'B'C'D'$. Chọn khẳng định đúng.
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{BB'}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{AC'}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{CD}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{AC}$ |
Cho hình chóp đều $S.ABCD$ có chiều cao $a$, $AC=2a$ (tham khảo hình bên).
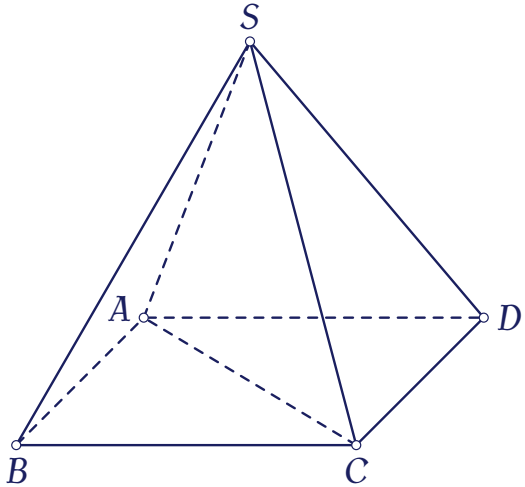
Khoảng cách từ $B$ đến mặt phẳng $(SCD)$ bằng
| $\dfrac{\sqrt{3}}{3}a$ | |
| $\sqrt{2}a$ | |
| $\dfrac{2\sqrt{3}}{3}a$ | |
| $\dfrac{\sqrt{2}}{2}a$ |
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, $SA$ vuông góc với đáy và $SA=AB$ (tham khảo hình bên).
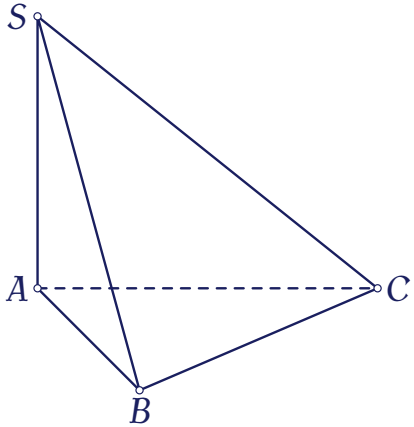
Góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ bằng
| $60^{\circ}$ | |
| $30^{\circ}$ | |
| $90^{\circ}$ | |
| $45^{\circ}$ |
Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa 2 vectơ $\overrightarrow{AB},\,\overrightarrow{A'C'}$.
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=45^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=60^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=30^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=90^\circ$ |
Cho 2 vectơ $\overrightarrow{u}=\overrightarrow{AB}$, $\overrightarrow{v}=\overrightarrow{AC}$. Khi đó $\big(\overrightarrow{u},\overrightarrow{v}\big)$ bằng
| $\widehat{ABC}$ | |
| $90^\circ$ | |
| $\widehat{ACB}$ | |
| $\widehat{BAC}$ |
Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân tại $A$, $AB=AC=a$ và $SA=SB=SC=a$. Tính $\overrightarrow{AB}\cdot\overrightarrow{SC}$.
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2\sqrt{3}}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2\sqrt{3}}{2}$ |
Cho 2 vectơ $\overrightarrow{u},\,\overrightarrow{v}$ có $\big|\overrightarrow{u}\big|=2$, $\big|\overrightarrow{v}\big|=5$ và $\big(\overrightarrow{u},\overrightarrow{v}\big)=30^\circ$. Tính $\overrightarrow{u}\cdot\overrightarrow{v}$.
| $\overrightarrow{u}\cdot\overrightarrow{v}=5\sqrt{2}$ | |
| $\overrightarrow{u}\cdot\overrightarrow{v}=5$ | |
| $\overrightarrow{u}\cdot\overrightarrow{v}=10$ | |
| $\overrightarrow{u}\cdot\overrightarrow{v}=5\sqrt{3}$ |
Cho hình lăng trụ $ABC.A'B'C'$. Chọn khẳng định đúng.
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AB}$ | |
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AC'}$ | |
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AB'}$ | |
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AC}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông và $SA\perp(ABCD)$.
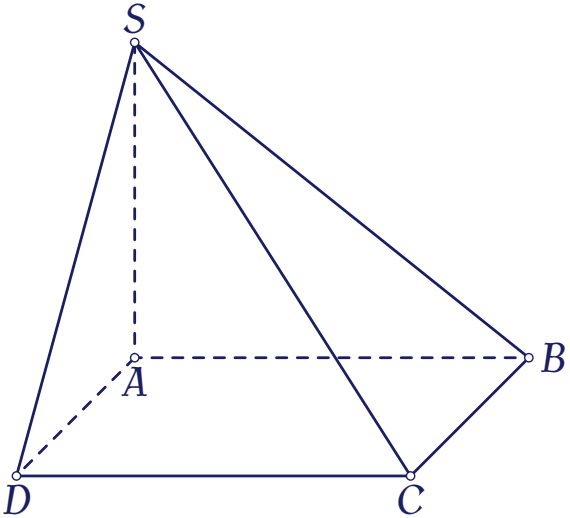
Khẳng định nào sau đây là đúng?
| $BC\perp(SAB)$ | |
| $BC\perp(SBD)$ | |
| $BC\perp(SCD)$ | |
| $BC\perp(SAC)$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
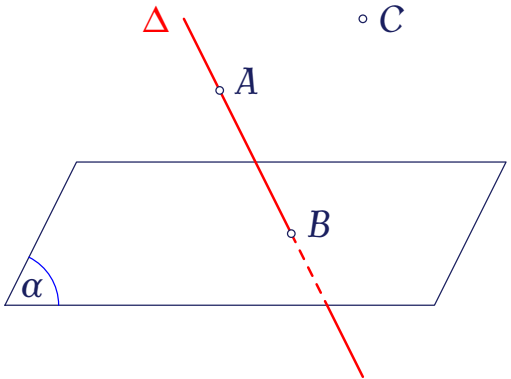
Giao tuyến của hai mặt phẳng $(\alpha)$ và $(ABC)$ có tồn tại không, nếu có thì giao tuyến đó đi qua điểm nào?
| $B$ | |
| $A$ | |
| $C$ | |
| Không tồn tại |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
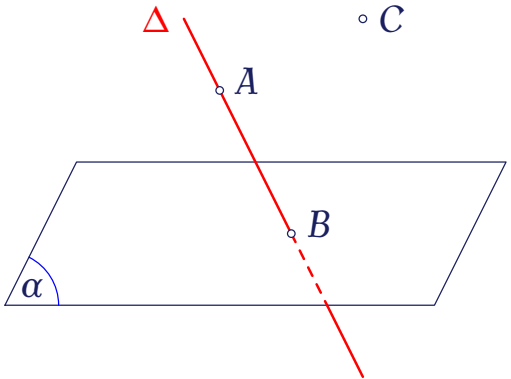
Mệnh đề nào sau đây là đúng?
| $\Delta\subset(\alpha)$ | |
| $\Delta\cap(\alpha)=A$ | |
| $C\in(\alpha)$ | |
| $\Delta\cap(\alpha)=B$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
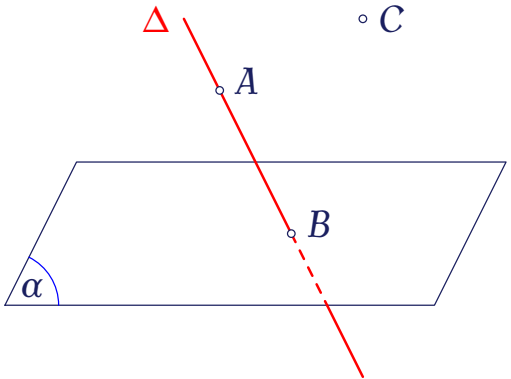
Xét mệnh đề "$B=\Delta\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
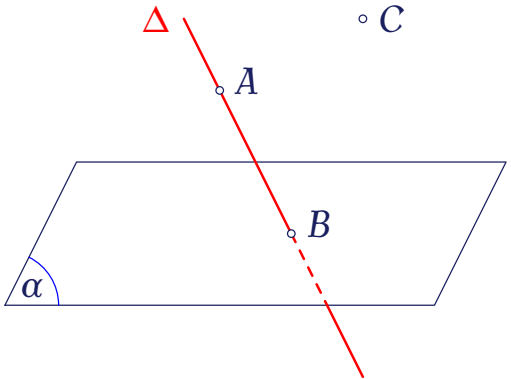
Xét mệnh đề "$C\ldots\ldots\Delta$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
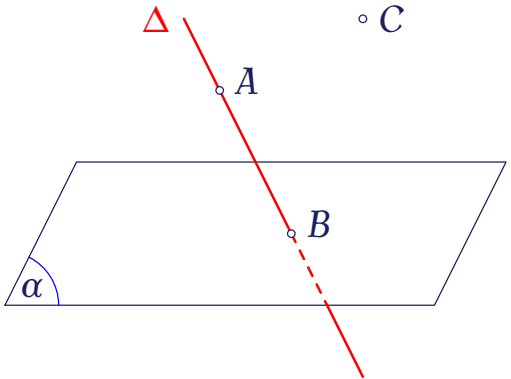
Xét mệnh đề "$A\ldots\ldots\Delta$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
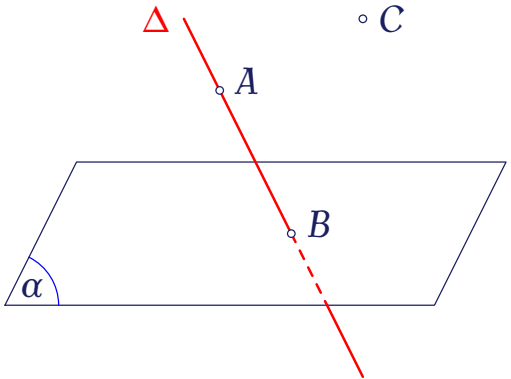
Xét mệnh đề "$A\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
