Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ có số đo
| $45^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a\sqrt{3}$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ có số đo
| $60^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $45^\circ$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SCA}$ | |
| $\widehat{SCB}$ | |
| $\widehat{SAC}$ | |
| $\widehat{ASC}$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SBA}$ | |
| $\widehat{SBC}$ | |
| $\widehat{SAB}$ | |
| $\widehat{ASB}$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ có số đo là
| $90^\circ$ | |
| $0^\circ$ | |
| $180^\circ$ | |
| $90$ |
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, $SA$ vuông góc với đáy và $SA=AB$ (tham khảo hình bên).
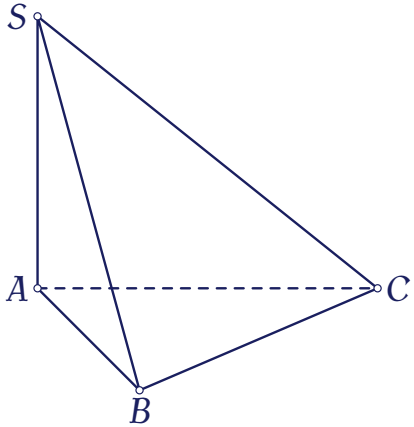
Góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ bằng
| $60^{\circ}$ | |
| $30^{\circ}$ | |
| $90^{\circ}$ | |
| $45^{\circ}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA$ vuông góc với mặt phẳng đáy, góc giữa $SA$ và mặt phẳng $(SBC)$ bằng $45^\circ$ (tham khảo hình bên).
Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3}{8}$ | |
| $\dfrac{3a^3}{8}$ | |
| $\dfrac{\sqrt{3}a^3}{12}$ | |
| $\dfrac{a^3}{4}$ |
Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$ (tham khảo hình vẽ).
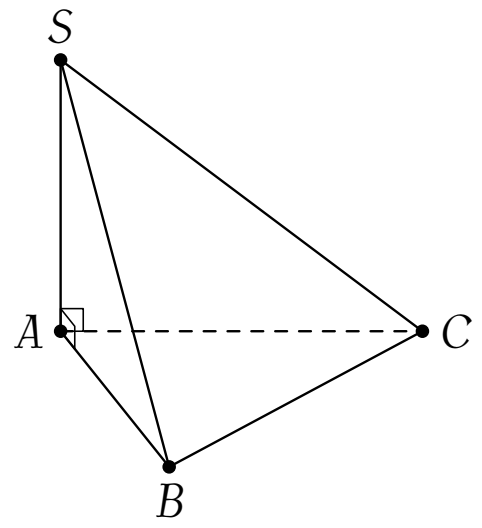
Biết thể tích của khối chóp $S.ABC$ là $\dfrac{a^3\sqrt{3}}{2}$ và góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ là góc nhọn $\alpha$. Chọn phát biểu đúng.
| $\alpha=60^{\circ}$ | |
| $\alpha=45^{\circ}$ | |
| $\alpha=30^{\circ}$ | |
| $\tan\alpha=\dfrac{\sqrt{3}}{2}$ |
Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$, $SA=2a$, tam giác $ABC$ vuông tại $B$, $AB=a\sqrt{3}$ và $BC=a$. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
Cho hình chóp $S.ABC$ có $SA\perp AB$ và $SA\perp BC$. Khẳng định nào sau đây không đúng?
| $AB\perp BC$ | |
| $SA\perp AC$ | |
| $SA\perp(ABC)$ | |
| $\big(SA,(ABC)\big)=90^\circ$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SC$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AC$ | |
| $BC$ | |
| $AB$ | |
| $SC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SB$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AB$ | |
| $BC$ | |
| $SB$ | |
| $AC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Khẳng định nào sau đây không đúng?
| $SB\perp BC$ | |
| $SA\perp AB$ | |
| $SA\perp AC$ | |
| $SA\perp BC$ |
Cho hình chóp $S.ABC$ có $SA=SB=SC=AB=AC=10$, $BC=10\sqrt{2}$. Gọi $M$ là trung điểm của $BC$ và $\alpha$ là góc giữa $AM$ và $SB$. Tính $\cos\alpha$.
| $\cos\alpha=\dfrac{1}{3}$ | |
| $\cos\alpha=\dfrac{2}{5}$ | |
| $\cos\alpha=0$ | |
| $\cos\alpha=\dfrac{2}{3}$ |
Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông cạnh $2a$, $SA\perp(ABCD)$ và $2a\sqrt{2}$.
- Chứng minh rằng $BD\perp(SAC)$.
- Tính góc tạo bởi $SC$ và $(SAD)$.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$, $SA$ vuông góc với mặt phẳng đáy và $SB$ tạo với mặt đáy một góc $60^\circ$. Gọi $M,\,N$ lần lượt là trung điểm của $SB$ và $BC$. Thể tích khối chóp $A.SCNM$ bằng
| $\dfrac{\sqrt{3}}{4}a^3$ | |
| $\dfrac{\sqrt{3}}{2}a^3$ | |
| $\dfrac{3\sqrt{3}}{4}a^3$ | |
| $\dfrac{3\sqrt{3}}{2}a^3$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Hình chiếu vuông góc của $S$ trên đáy là điểm $H$ trên cạnh $AC$ sao cho $AH=\dfrac{2}{3}AC$; mặt phẳng $(SBC)$ tạo với đáy một góc $60^{\circ}$. Thể tích khối chóp $S.ABC$ là
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3\sqrt{3}}{48}$ | |
| $\dfrac{a^3\sqrt{3}}{36}$ | |
| $\dfrac{a^3\sqrt{3}}{24}$ |
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình vuông cạnh $a$, $SA\perp\left(ABCD\right)$ và $SA=a$.
Góc giữa hai đường thẳng $SD$ và $BC$ bằng
| $60^{\circ}$ | |
| $45^{\circ}$ | |
| $90^{\circ}$ | |
| $30^{\circ}$ |
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(a\), cạnh bên \(SA=2a\) và vuông góc với mặt đáy. Gọi \(M,\,N\) lần lượt là hình chiếu vuông góc của \(A\) trên các đường thẳng \(SB\), \(SC\).
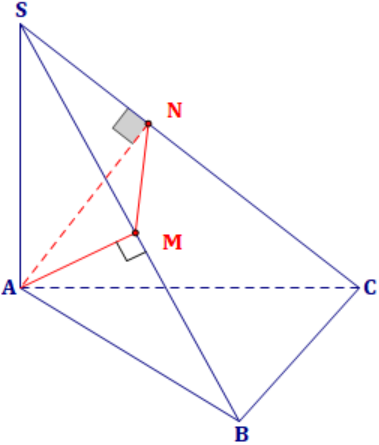
 Tính thể tích của khối chóp \(A.BCNM\).
Tính thể tích của khối chóp \(A.BCNM\).
