Có bao nhiêu số thực $x$ thỏa mãn $9^{\log_3x}=4$?
| $4$ | |
| $0$ | |
| $2$ | |
| $1$ |
Có bao nhiêu số nguyên $y$ sao cho tồn tại số thực $x$ thỏa mãn $\log_2\left(4444+4x-2x^2\right)=2\cdot2^{y^2}+y^2+x^2-2x-2220$?
| $13$ | |
| $9$ | |
| $11$ | |
| $7$ |
Tìm số nghiệm của phương trình $$4^{x-1}+2^{x+3}-4=0$$
| \(1\) | |
| \(0\) | |
| \(3\) | |
| \(2\) |
Tìm số nghiệm của phương trình $$2^{x^3+2x^2-3x}\cdot3^{x-1}=1$$
| \(2\) | |
| \(1\) | |
| \(0\) | |
| \(3\) |
Tìm số nghiệm của phương trình $$2^{x^2-5x+6}+2^{1-x^2}=2\cdot2^{6-5x}+1$$
| \(1\) | |
| \(2\) | |
| \(3\) | |
| \(4\) |
Phương trình \(3^{1-x}=2+\left(\dfrac{1}{9}\right)^x\) có bao nhiêu nghiệm âm?
| \(0\) | |
| \(1\) | |
| \(2\) | |
| \(3\) |
Phương trình \(9^x-6^x=2^{2x+1}\) có bao nhiêu nghiệm âm?
| \(3\) | |
| \(0\) | |
| \(1\) | |
| \(2\) |
Tìm số nghiệm thực của phương trình $$4^x-2^{x+2}+3=0$$
| \(3\) | |
| \(2\) | |
| \(1\) | |
| \(0\) |
Tìm số nghiệm của phương trình $$16^x+3\cdot4^x+2=0.$$
| \(0\) | |
| \(2\) | |
| \(1\) | |
| \(3\) |
Số nghiệm của phương trình \(2^{2x^2-7x+5}=1\) là
| \(1\) | |
| \(0\) | |
| \(3\) | |
| \(2\) |
Phương trình \(\left(\sqrt{5}\right)^{x^2+4x+6}=\log_2{128}\) có bao nhiêu nghiệm?
| \(1\) | |
| \(3\) | |
| \(2\) | |
| \(0\) |
Số nghiệm thực phân biệt của phương trình \(2^{x^2}=\sqrt{3}\) là
| \(0\) | |
| \(2\) | |
| \(1\) | |
| \(3\) |
Phương trình $3^{2x}-(m+1)3^x+m=0$ có đúng một nghiệm khi
| $m=0$ | |
| $m>0$ | |
| $m>0$, $m\neq1$ | |
| $m=1$ hoặc $m\leq0$ |
Tổng tất cả các nghiệm của phương trình $9^{x^2-2x-7}=3$ là
| $2$ | |
| $7$ | |
| $-7$ | |
| $4$ |
Cho phương trình $9^x-2\cdot3^{x+2}-1=0$. Đặt $t=3^x$, $t>0$, phương trình đã cho trở thành phương trình nào dưới đây?
| $2t^2-9t-2=0$ | |
| $t^2-9t-1=0$ | |
| $t^2-18t-1=0$ | |
| $9t^2-2t-9=0$ |
Phương trình $3^{1-x}=9$ có nghiệm là
| $x=-1$ | |
| $x=-2$ | |
| $x=1$ | |
| $x=2$ |
Có bao nhiêu giá trị nguyên của tham số $m\in(-10;100)$ để tồn tại các số thực dương $a,\,b,\,x,\,y$ thỏa mãn $a\neq1$, $b\neq1$ và $a^{2x}=b^y=(ab)^{x+my}$?
| $0$ | |
| $100$ | |
| $99$ | |
| $98$ |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
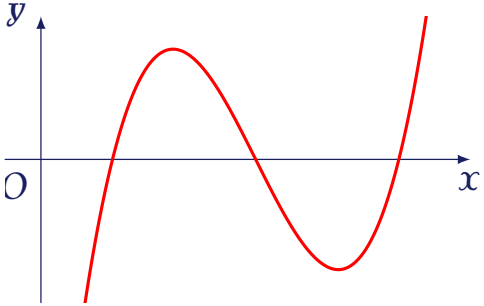
Số các giá trị nguyên của tham số $m\in(-2019;2023]$ để phương trình $4^{f(x)}-(m-1)2^{f(x)+1}+2m-3=0$ có đúng ba nghiệm là
| $2020$ | |
| $2019$ | |
| $2021$ | |
| $2022$ |
Nghiệm của phương trình $2^{x+1}=4$ là
| $x=3$ | |
| $x=1$ | |
| $x=2$ | |
| $x=0$ |
Nghiệm của phương trình $2^{2x-1}=8$ là
| $x=\dfrac{5}{2}$ | |
| $x=3$ | |
| $x=2$ | |
| $x=\dfrac{3}{2}$ |
