Giá trị của tham số thực \(m\) bằng bao nhiêu để bình phương số phức \(z=\dfrac{(m+9i)(1+i)}{2}\) là số thực?
| Không có giá trị \(m\) thỏa | |
| \(m=-9\) | |
| \(m=9\) | |
| \(m=\pm9\) |
Số phức liên hợp của số phức \(z=(1+i)^{15}\) là
| \(\overline{z}=128+128i\) | |
| \(\overline{z}=128-128i\) | |
| \(\overline{z}=-1\) | |
| \(\overline{z}=-128-128i\) |
Cho số phức \(z=a+bi\). Số phức \(z^2\) có phần thực và phần ảo là
| \(a^2+b^2\) và \(2a^2b^2\) | |
| \(a+b\) và \(a^2b^2\) | |
| \(a^2-b^2\) và \(2ab\) | |
| \(a-b\) và \(ab\) |
Cho số phức \(z\) thỏa mãn \(|z|=2\) và \(\left|z^2+1\right|=4\). Tính \(\left|z+\overline{z}\right|+\left|z-\overline{z}\right|\).
| \(3+\sqrt{7}\) | |
| \(3+2\sqrt{2}\) | |
| \(7+\sqrt{3}\) | |
| \(16\) |
Cho số phức \(z=1-\mathrm{i}\). Biểu diễn số phức \(z^2\) là điểm
| \(N(-2;0)\) | |
| \(Q(0;-2)\) | |
| \(P(2;0)\) | |
| \(M(1;2)\) |
Cho số phức \(z=2+\mathrm{i}\). Tính môđun của số phức \(w=z^2-1\).
| \(|w|=2\sqrt{5}\) | |
| \(|w|=\sqrt{5}\) | |
| \(|w|=5\sqrt{5}\) | |
| \(|w|=20\) |
Cho \(z_1,\,z_2\) là hai số phức tùy ý. Khẳng định nào dưới đây sai?
| \(z\cdot\overline{z}=|z|^2\) | |
| \(\left|z_1+z_2\right|=\left|z_1\right|+\left|z_2\right|\) | |
| \(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}\) | |
| \(\left|z_1\cdot z_2\right|=\left|z_1\right|\cdot\left|z_2\right|\) |
Tổng phần thực và phần ảo của số phức \(z=(1+\mathrm{i})^2-(3+3\mathrm{i})\) bằng
| \(\sqrt{10}\) | |
| \(-4\) | |
| \(4\) | |
| \(-3-\mathrm{i}\) |
Có bao nhiêu số phức \(z\) thỏa mãn \(z^2+|z|=0\)?
| \(1\) | |
| \(4\) | |
| \(2\) | |
| \(3\) |
Nghịch đảo của số phức \(z=(1-2\mathrm{i})^2\) có môđun bằng
| \(\dfrac{1}{\sqrt{5}}\) | |
| \(\dfrac{1}{25}\) | |
| \(\sqrt{5}\) | |
| \(\dfrac{1}{5}\) |
Tìm môđun của số phức \(z=(-6+8\mathrm{i})^2\).
| \(|z|=4\sqrt{527}\) | |
| \(|z|=2\sqrt{7}\) | |
| \(|z|=100\) | |
| \(|z|=10\) |
Tính môđun của số phức $$z=(2-\mathrm{i})(1+\mathrm{i})^2+1$$
| \(|z|=4\) | |
| \(|z|=5\) | |
| \(|z|=2\sqrt{5}\) | |
| \(|z|=25\) |
Tìm số phức liên hợp của số phức $$z=1-3\mathrm{i}+(1-\mathrm{i})^2$$
| \(\overline{z}=-1-5\mathrm{i}\) | |
| \(\overline{z}=1-5\mathrm{i}\) | |
| \(\overline{z}=1+5\mathrm{i}\) | |
| \(\overline{z}=5-\mathrm{i}\) |
Cho hai số phức $z_1=2-i$ và $z_2=1+3i$. Phần thực của số phức $z_1-z_2$ bằng
| $3$ | |
| $-4$ | |
| $1$ | |
| $-1$ |
Cho hai số phức $z_1=3-i$ và $z_2=-2+5i$. Khi đó mô-đun của số phức $z=z_1+z_2$ bằng
| $\sqrt{17}$ | |
| $2\sqrt{17}$ | |
| $\sqrt{39}$ | |
| $\sqrt{10}$ |
Xét số phức $z$ thỏa mãn $|z+3-2i|+|z-3+i|=3\sqrt{5}$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|+|z-1-3i|$. Khi đó
| $M=\sqrt{26}+2\sqrt{5}$, $m=3\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{26}+2\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=3\sqrt{2}$ |
Cho số phức $z=a+bi$ ($a,\,b\in\mathbb{R}$) thỏa mãn $z-4=(1+i)|z|-(4+3z)i$. Giá trị của biểu thức $P=a-3b$ bằng
| $P=-2$ | |
| $P=6$ | |
| $P=2$ | |
| $P=-6$ |
Gọi $A,\,B,\,C$ là điểm biểu diễn cho các số phức $z_1=-2+3i$, $z_2=-4-2i$, $z_3=3+i$. Khi đó tọa độ trọng tâm $G$ của tam giác $ABC$ là
| $\left(-1;-\dfrac{2}{3}\right)$ | |
| $\left(-1;\dfrac{2}{3}\right)$ | |
| $\left(1;-\dfrac{2}{3}\right)$ | |
| $\left(1;\dfrac{2}{3}\right)$ |
Điểm $M$ trong hình vẽ bên là điểm biểu diễn cho số phức $z$.
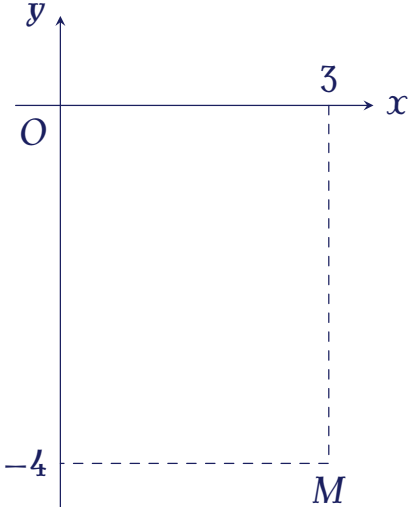
Phần ảo của số phức $(1+i)z$ bằng
| $7$ | |
| $-7$ | |
| $-1$ | |
| $1$ |
Cho số phức $z=1-3i$. Số phức $w=(1-i)z+\overline{z}$ có phần ảo bằng
| $1$ | |
| $-1$ | |
| $-i$ | |
| $i$ |
