Số nghiệm nguyên của bất phương trình $\log_4(2x+3)< 2$ là
| $7$ | |
| $8$ | |
| $9$ | |
| $10$ |
Số $\dfrac{\sqrt[3]{16}}{8}$ viết dưới dạng lũy thừa với số mũ hữu tỉ là
| $2^{\tfrac{13}{3}}$ | |
| $2^{-\tfrac{13}{3}}$ | |
| $2^{\tfrac{5}{3}}$ | |
| $2^{-\tfrac{5}{3}}$ |
Cho khối hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=a$, $AD=\sqrt{2}a$, $AA'=2a$. Thể tích khối hộp đã cho bằng
| $4a^3$ | |
| $2\sqrt{2}a^3$ | |
| $\sqrt{2}a^3$ | |
| $2a^3$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
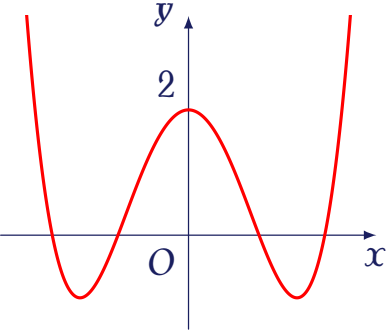
Số nghiệm của phương trình $f(x)-1=0$ là
| $2$ | |
| $1$ | |
| $4$ | |
| $3$ |
Cho hàm số $y=ax^3-3x^2+b$ ($a\neq0$) có bảng biến thiên như sau:
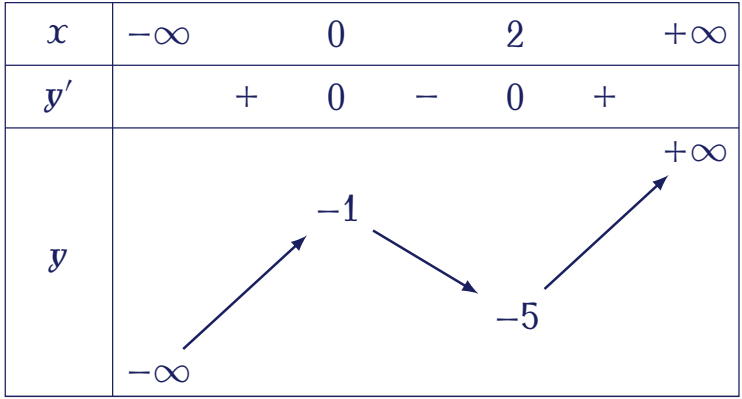
Mệnh đề nào dưới đây đúng?
| $a>0,\,b< 0$ | |
| $a< 0,\,b>0$ | |
| $a>0,\,b>0$ | |
| $a< 0,\,b< 0$ |
Đạo hàm của hàm số $y=(x+1)^\pi$ là
| $y'=\pi(x+1)^\pi$ | |
| $y'=(\pi-1)(x+1)^{\pi-1}$ | |
| $y'=\pi(x+1)^{\pi-1}$ | |
| $y'=(x+1)^{\pi-1}$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AB=BC=a$ và $AA'=6a$. Thể tích của khối lăng trụ $ABC.A'B'C'$ bằng
| $6a^3$ | |
| $2a^3$ | |
| $3a^3$ | |
| $a^3$ |
Cho một mặt cầu có bán kính là $5$cm. Một mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn (xem hình minh họa) cách tâm mặt cầu đã cho là $3$cm.
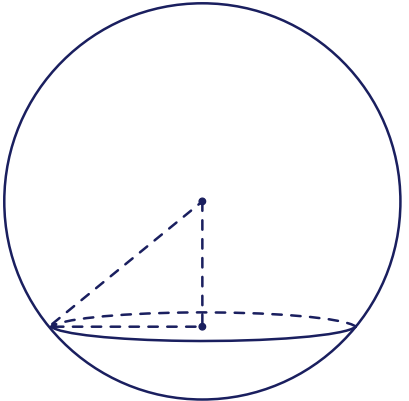
Bán kính đường tròn giao tuyến bằng
| $3$cm | |
| $4$cm | |
| $2$cm | |
| $5$cm |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA$ vuông góc với mặt phẳng đáy và $SA=9a$. Thể tích khối chóp $S.ABCD$ bằng
| $a^3$ | |
| $27a^3$ | |
| $9a^3$ | |
| $3a^3$ |
Cho hàm số $y=f(x)$ có đồ thị là đường cong trong hình bên.
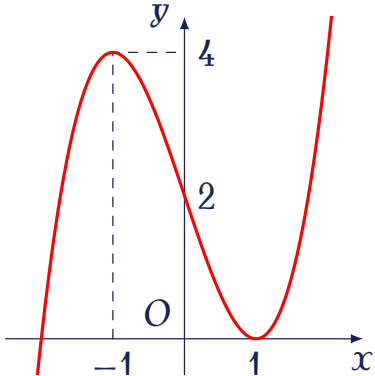
Giá trị của tham số $m$ để phương trình $f(x)+1=m$ có ba nghiệm phân biệt là
| $0< m< 4$ | |
| $1< m< 5$ | |
| $-1< m< 4$ | |
| $0< m< 5$ |
Đạo hàm của hàm số $y=\ln\big(x^2+2\big)$ là
| $y'=\dfrac{1}{x^2+2}$ | |
| $y'=\dfrac{x}{x^2+2}$ | |
| $y'=\dfrac{2}{x^2+2}$ | |
| $y'=\dfrac{2x}{x^2+2}$ |
Cho hàm số $y=f(x)$ có bảng biến thiên trên đoạn $[-1;3]$ như sau:
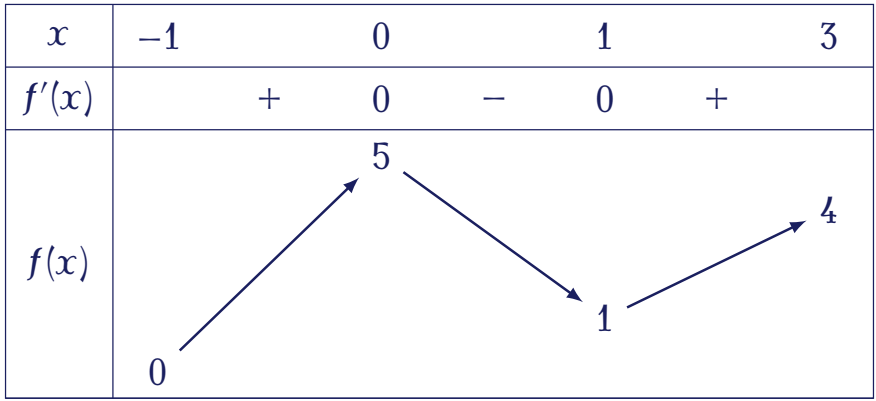
Giá trị lớn nhất của hàm số đã cho trên đoạn $[-1;3]$ bằng
| $1$ | |
| $4$ | |
| $0$ | |
| $5$ |
Có bao nhiêu hình đa diện trong các hình dưới đây?
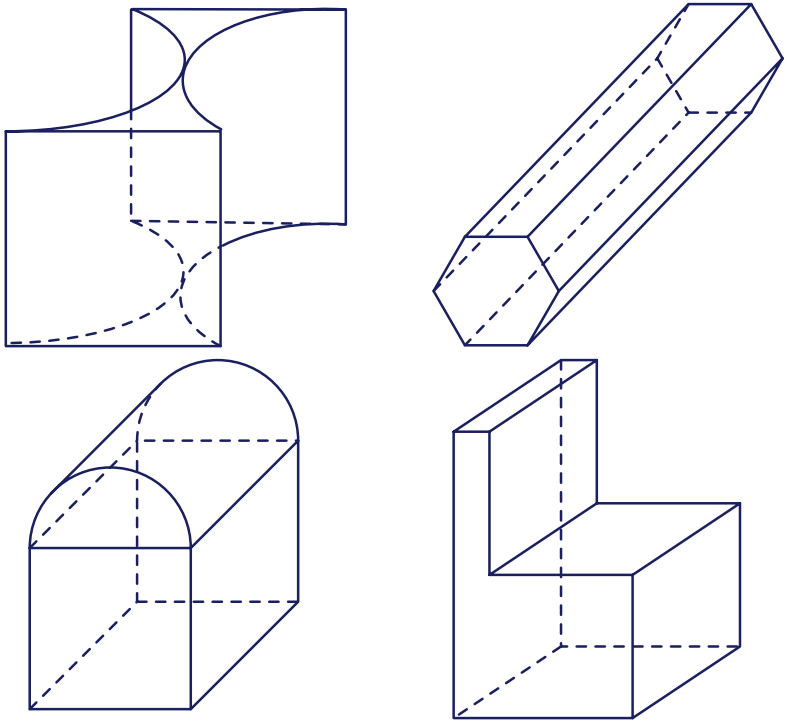
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
Cho hình nón có độ dài đường sinh là $4$ và bán kính là $2$. Diện tích xung quanh hình nón đã cho bằng
| $32\pi$ | |
| $4\pi$ | |
| $16\pi$ | |
| $8\pi$ |
Khối đa diện đều như hình bên là khối đa diện nào sau đây?
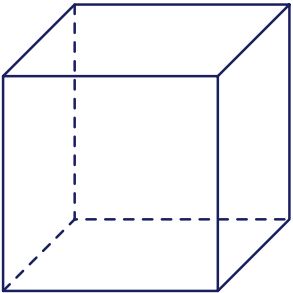
| Khối lập phương | |
| Khối tứ diện đều | |
| Khối mười hai mặt đều | |
| Khối bát diện đều |
Cho hàm số $y=f(x)$ có bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số đã cho bằng
| $3$ | |
| $0$ | |
| $1$ | |
| $2$ |
Cho khối trụ có bán kính đáy là $5$ và chiều cao là $3$. Thể tích của khối trụ đã cho bằng
| $5\pi$ | |
| $75\pi$ | |
| $30\pi$ | |
| $45\pi$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
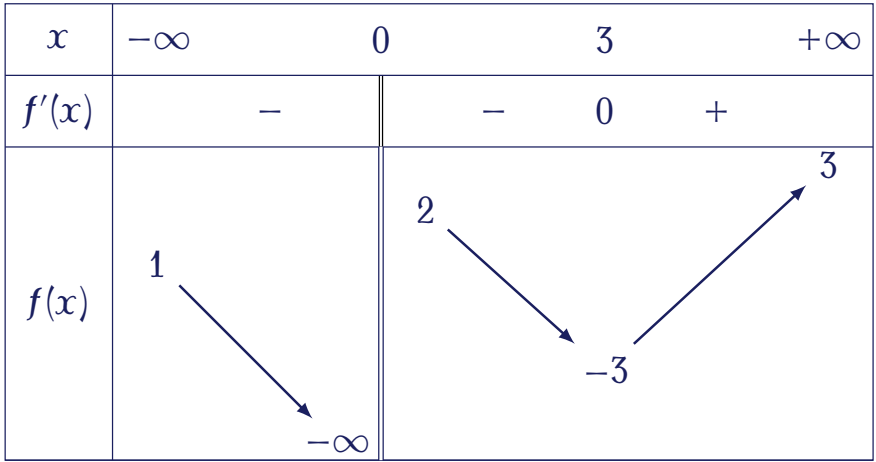
Tiệm cận đứng của đồ thị hàm số đã cho là
| $x=3$ | |
| $x=2$ | |
| $x=0$ | |
| $x=1$ |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên dưới.
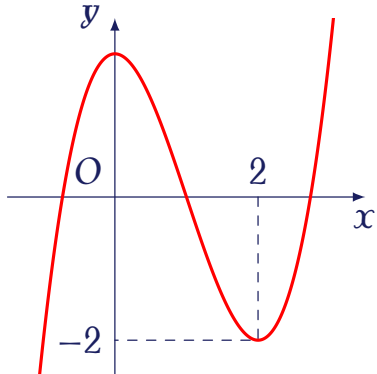
Hàm số đã cho đồng biến trên khoảng nào sau đây?
| $(2;+\infty)$ | |
| $(-2;2)$ | |
| $(0;2)$ | |
| $(-\infty;2)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
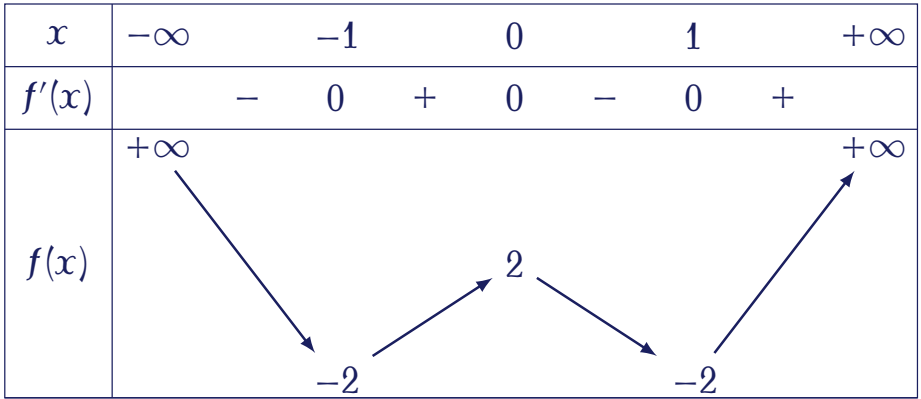
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(-\infty;1)$ | |
| $(0;1)$ | |
| $(-1;0)$ | |
| $(-2;+\infty)$ |
