Cho $u=u(x)$, $v=v(x)$ và $k$ là hằng số. Mệnh đề nào sau đây là sai?
| $(k.u)^{\prime}=k.u'$ | |
| $\left(\dfrac{1}{v}\right)^{\prime}=-\dfrac{1}{v^2}$ | |
| $\left(u^n\right)^{\prime}=n.u^{n-1}.u'$ | |
| $\left(\sqrt{u}\right)^{\prime}=\dfrac{u'}{2\sqrt{u}}$ |
Một chất điểm chuyển động có phương trình $s=t^3-2t$ ($t$ tính bằng giây, $s$ tính bằng mét). Tính vận tốc của chất điểm tại thời điểm $t_0=4$ (giây)?
| $64$m/s | |
| $46$m/s | |
| $56$m/s | |
| $22$m/s |
Biết $\left(x^5-3x^4+2019\right)^{\prime}=ax^4+bx^3$. Tìm $S=a+b$.
| $S=-7$ | |
| $S=7$ | |
| $S=17$ | |
| $S=12$ |
Cho $f(x)=\dfrac{x^2-x+2}{x+1}$. Tính $f'(-2)$.
| $-3$ | |
| $-5$ | |
| $1$ | |
| $0$ |
Mệnh đề nào sau đây là sai?
| $(\cos x)^{\prime}=-\sin x$ | |
| $(\sin x)^{\prime}=-\cos x$ | |
| $(\cot x)^{\prime}=-\dfrac{1}{\sin^2x}$ | |
| $(\tan x)^{\prime}=\dfrac{1}{\cos^2x}$ |
Tính đạo hàm của hàm số $y=\cot3x$.
| $y'=-\dfrac{3}{\sin^2x}$ | |
| $y'=\dfrac{3}{\sin^23x}$ | |
| $y'=-\dfrac{3}{\sin^33x}$ | |
| $y'=-\dfrac{3}{\sin^23x}$ |
Viết phương trình tiếp tuyến của đồ thị hàm số $y=f(x)=-x^3+x$ tại điểm $M(-2;6)$.
| $y=-11x-16$ | |
| $y=-11x-28$ | |
| $y=-11x+28$ | |
| $y=-11x+16$ |
Cho hàm số $f(x)=x^3-2x^2+x+3$. Nghiệm của bất phương trình $f'(x)< 0$ là
| $1< x< 3$ | |
| $-1< x< \dfrac{1}{3}$ | |
| $\dfrac{1}{3}< x< 1$ | |
| $-\dfrac{1}{3}< x< 1$ |
Ông An muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong phía trên là một Parabol. Giá $1m^2$ của rào sắt là $700 000$ đồng.
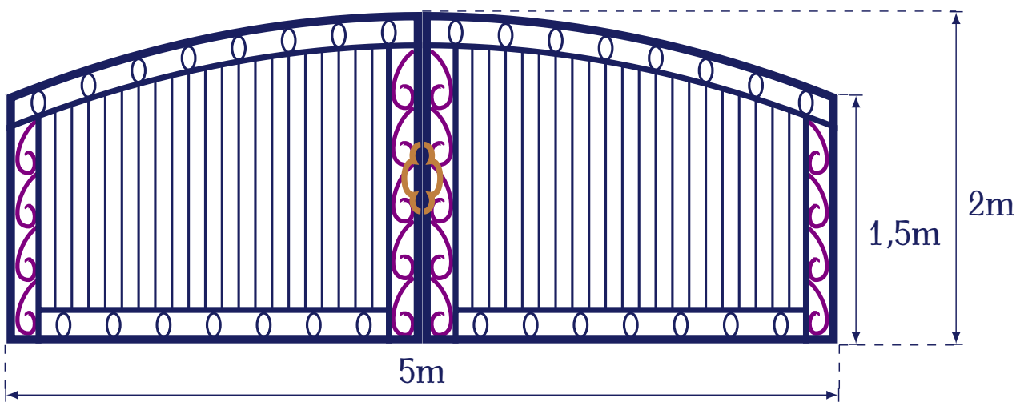
Hỏi ông An phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng nghìn).
(Cảm ơn tác giả đã vẽ hình và trình bày, cảm ơn TS. Trần Lê Nam đã chia sẻ)
| $6 520 000$ đồng | |
| $6 320 000$ đồng | |
| $6 417 000$ đồng | |
| $6 620 000$ đồng |
Cho hàm số $y=f(x)$ là hàm liên tục có tích phân trên $[0;2]$ thỏa điều kiện $f\left(x^2\right)=6x^4+\displaystyle\displaystyle\int\limits_{0}^{2}xf(x)\mathrm{\,d}x$. Tính $I=\displaystyle\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x$.
| $I=-8$ | |
| $I=-24$ | |
| $I=-32$ | |
| $I=-6$ |
Gọi $S$ là tập hợp tất cả các số phức $z$ để số phức $w=|z|-\dfrac{1}{z-1}$ có phần ảo bằng $\dfrac{1}{4}$. Biết rằng $\left|z_1-z_2\right|=3$ với $z_1,\,z_2\in S$, giá trị nhỏ nhất của $\left|z_1+2z_2\right|$ bằng
| $\sqrt{5}-\sqrt{3}$ | |
| $3\sqrt{5}-3$ | |
| $2\sqrt{5}-2\sqrt{3}$ | |
| $3\sqrt{5}-3\sqrt{2}$ |
Trong không gian $Oxyz$, cho hai điểm $M(-2;-2;1)$, $A(1;2;-3)$ và đường thẳng $d\colon\dfrac{x+1}{2}=\dfrac{y-5}{2}=\dfrac{z}{-1}$. Gọi $\overrightarrow{u}=(1;a;b)$ là một vectơ chỉ phương của đường thẳng $\Delta$ đi qua $M$, $\Delta$ vuông góc với đường thẳng $d$ đồng thời cách điểm $A$ một khoảng nhỏ nhất. Giá trị của $a+2b$ là
| $1$ | |
| $2$ | |
| $3$ | |
| $4$ |
Trong không gian $Oxyz$, gọi mặt phẳng $(P)\colon7x+by+cz+d=0$ (với $b,\,c,\,d\in\mathbb{R}$, $c< 0$) đi qua điểm $A(1;3;5)$. Biết mặt phẳng $(P)$ song song với trục $Oy$ và khoảng cách từ gốc tọa độ đến mặt phẳng $(P)$ bằng $3\sqrt{2}$. Tính $T=b+c+d$.
| $T=61$ | |
| $T=78$ | |
| $T=7$ | |
| $T=-4$ |
Cho hàm số $f(x)=ax^3+bx^2-36x+c$ ($a\neq0$, $a,\,b,\,c\in\mathbb{R}$), có hai điểm cực trị là $-6$ và $2$. Gọi $y=g(x)$ là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=f(x)$. Diện tích hình phẳng giới hạn bởi hai đường $y=f(x)$ và $y=g(x)$ bằng
| $160$ | |
| $672$ | |
| $128$ | |
| $64$ |
Cho số phức $z=x+iy$ (với $x,\,y\in\mathbb{R}$) thỏa mãn $2z-5i\cdot\overline{z}=-14-7i$. Tính $x+y$.
| $1$ | |
| $7$ | |
| $-1$ | |
| $5$ |
Biết phương trình $z^2+mz+n=0$ ($m,\,n\in\mathbb{R}$) có một nghiệm là $1-3i$. Tính $n+3m$.
| $4$ | |
| $3$ | |
| $16$ | |
| $6$ |
Trong không gian $Oxyz$, cho $(S)\colon x^2+y^2+z^2-4x-2y+10z-14=0$. Mặt phẳng $(P)\colon-x+4z+5=0$ cắt mặt cầu $(S)$ theo một đường tròn $(\mathscr{C})$. Tọa độ tâm $H$ của $(\mathscr{C})$ là
| $H(1;1;-1)$ | |
| $H(-3;1;-2)$ | |
| $H(9;1;1)$ | |
| $H(-7;1;-3)$ |
Tính nguyên hàm $\displaystyle\displaystyle\int\dfrac{\left(\ln x+2\right)\mathrm{d}x}{x\ln x}$ bằng cách đặt $t=\ln x$ ta được nguyên hàm nào sau đây?
| $\displaystyle\displaystyle\int\dfrac{t\mathrm{\,d}t}{t-2}$ | |
| $\displaystyle\displaystyle\int(t+2)\mathrm{\,d}t$ | |
| $\displaystyle\displaystyle\int\left(1+\dfrac{2}{t}\right)\mathrm{\,d}t$ | |
| $\displaystyle\displaystyle\int\dfrac{(t+2)\mathrm{\,d}t}{t^2}$ |
Trong không gian $Oxyz$, mặt phẳng $(\alpha)$ đi qua hai điểm $A(1;0;0)$, $B(2;2;0)$ và vuông góc với mặt phẳng $(P)\colon x+y+z-2=0$ có phương trình là
| $x+y-2z-4=0$ | |
| $2x-y-3z-2=0$ | |
| $x+y+z-1=0$ | |
| $2x-y-z-2=0$ |
Cho $\displaystyle\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{4}}\cos4x\cos x\mathrm{\,d}x=\dfrac{\sqrt{2}}{a}+\dfrac{b}{c}$ với $a,\,b,\,c$ là các số nguyên, $c< 0$ và $\dfrac{b}{c}$ tối giản. Tổng $a+b+c$ bằng
| $-77$ | |
| $-17$ | |
| $103$ | |
| $43$ |
