Cho hàm số $f(x)$ có đạo hàm trên $\mathbb{R}$ thỏa mãn $f(1)=-13$ và $f'(x)=15x^2-16x-1+\displaystyle\int\limits_{0}^{1}xf(x)\mathrm{\,d}x$. Khi đó $\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x$ bằng
| $\dfrac{26}{3}$ | |
| $-\dfrac{64}{3}$ | |
| $-\dfrac{35}{4}$ | |
| $\dfrac{15}{4}$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa mãn $f(x)=3x^2-2x+3+4\displaystyle\int\limits_{0}^{1}xf\left(x^2\right)\mathrm{\,d}x$. Khi đó $\displaystyle\int\limits_{2}^{3}f(x)\mathrm{\,d}x$ bằng
| $17$ | |
| $11$ | |
| $14$ | |
| $21$ |
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ thỏa mãn $f(x)=x^2-3x+2\displaystyle\int\limits_{0}^{1}f(x)f'(x)\mathrm{\,d}x$. Khi đó $\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x$ bằng
| $\dfrac{10}{3}$ | |
| $-\dfrac{10}{3}$ | |
| $\dfrac{26}{15}$ | |
| $-\dfrac{26}{15}$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=\sin x+2\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\cos x\cdot f(x)\mathrm{\,d}x$. Giá trị $f\left(-\dfrac{\pi}{2}\right)$ bằng
| $-\pi$ | |
| $-1$ | |
| $-2$ | |
| $0$ |
Cho hàm số $f(x)$ xác định và liên tục trên đoạn $[0;1]$ thỏa mãn $f(x)=x^3+\displaystyle\int\limits_{0}^{1}x^3f\left(x^2\right)\mathrm{\,d}x$, $\forall x\in[0;1]$. Tính tích phân $\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$.
| $\dfrac{1}{4}$ | |
| $\dfrac{4}{15}$ | |
| $\dfrac{13}{20}$ | |
| $\dfrac{23}{60}$ |
Cho hàm số $f(x)$ thỏa mãn $f(x)=x\mathrm{e}^x+\displaystyle\int\limits_{0}^{2}\left(f(x)+f'(x)-\mathrm{e}^x-1\right)\mathrm{\,d}x$. Tính tích phân $\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$.
| $2\mathrm{e}^2-1$ | |
| $-2\mathrm{e}^2-1$ | |
| $-2\mathrm{e}^2+1$ | |
| $2\mathrm{e}^2+1$ |
Cho hàm số $f(x)$ xác định và liên tục trên $[0;+\infty)$ thỏa mãn $f(x)=x\sqrt{x}+\displaystyle\int\limits_{0}^{1}xf(x)\mathrm{\,d}x$. Tính tích phân $\displaystyle\int\limits_{0}^{4}f(x)\mathrm{\,d}x$.
| $\dfrac{528}{35}$ | |
| $\dfrac{488}{35}$ | |
| $\dfrac{408}{35}$ | |
| $\dfrac{368}{35}$ |
Cho hàm số $f(x)$ xác định và liên tục trên khoảng $(0;+\infty)$ thỏa mãn $f(x)=\dfrac{1}{x}+\displaystyle\int\limits_{1}^{2}xf(x)\mathrm{\,d}x$, $\forall x\in(0;+\infty)$. Tính tích phân $\displaystyle\int\limits_{1}^{\mathrm{e}}f(x)\mathrm{\,d}x$.
| $\dfrac{5-2\mathrm{e}}{3}$ | |
| $3-2\mathrm{e}$ | |
| $2+2\mathrm{e}$ | |
| $1-2\mathrm{e}$ |
Xét hàm số $f(x)=\mathrm{e}^x+\displaystyle\int\limits_{0}^{1}xf(x)\mathrm{\,d}x$. Giá trị $f\left(\ln5620\right)$ bằng
| $5622$ | |
| $5620$ | |
| $5618$ | |
| $5621$ |
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y=\dfrac{3}{4}x^4-(m-1)x^2-\dfrac{1}{4x^4}$ đồng biến trên khoảng $(0;+\infty)$?
| $4$ | |
| $2$ | |
| $1$ | |
| $3$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f(x)+x f'(x)=4x^3-6x^2$, $\forall x\in\mathbb{R}$. Diện tích hình phẳng giới hạn bởi các đường $y=f(x)$ và $y=f'(x)$ bằng
| $\dfrac{7}{12}$ | |
| $\dfrac{45}{4}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{71}{6}$ |
Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn $[-10;10]$ để hàm số $$y=\big|-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\big|$$đồng biến trên khoảng $(0;1)$
| $21$ | |
| $10$ | |
| $8$ | |
| $2$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Gọi $F(x)$ và $G(x)$ là hai nguyên hàm của $f(x)$ thỏa mãn $2F(3)+G(3)=9+2F(-1)+G(-1)$. Khi đó $\displaystyle\displaystyle\int\limits_0^2\big(x^2+f(3-2x)\big)\mathrm{\,d}x$ bằng
| $\dfrac{25}{6}$ | |
| $\dfrac{7}{6}$ | |
| $\dfrac{43}{6}$ | |
| $3$ |
Nếu $\displaystyle\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x=5$ và $\displaystyle\displaystyle\int\limits_{0}^{1}g(x)\mathrm{\,d}x=4$ thì $\displaystyle\displaystyle\int\limits_{0}^{1}\big[f(x)-g(x)\big]\mathrm{\,d}x$ bằng
| $54$ | |
| $20$ | |
| $9$ | |
| $1$ |
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số $y=x^5$, trục hoành và hai đường thẳng $x=-1$, $x=1$ bằng
| $\dfrac{3}{2}$ | |
| $\dfrac{1}{3}$ | |
| $7$ | |
| $5$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Một mảnh vườn hình elip có độ dài trục lớn $8$m và độ dài trục nhỏ $6$m. Người ta cần trồng rau trên dải đất rộng $4$m như hình vẽ.
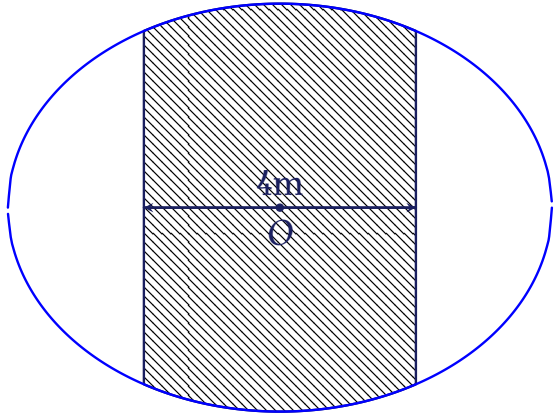
Hỏi cần bao nhiêu tiền để trồng rau trên dải đất đó, biết rằng kinh phí trồng rau là $70000$ đồng/m$^2$?
| $1.607.107$ đồng | |
| $803.553$ đồng | |
| $267.851$ đồng | |
| $2.638.938$ đồng |
Tính tích phân $\displaystyle\int\limits_{1}^{2}\left(x^2+4x+\dfrac{4}{x^2}\right)\mathrm{\,d}x$.
Tính tích phân $\displaystyle\int\limits_{0}^{1}(2x+1)^5\mathrm{\,d}x$.
Tính tích phân $I=\displaystyle\int\limits_{0}^{1}x(1+x)^2\mathrm{\,d}x$.
