Cho $a$ và $b$ là hai số thực dương khác $1$ và các hàm số $y=a^x$, $y=b^x$ có đồ thị như hình bên.
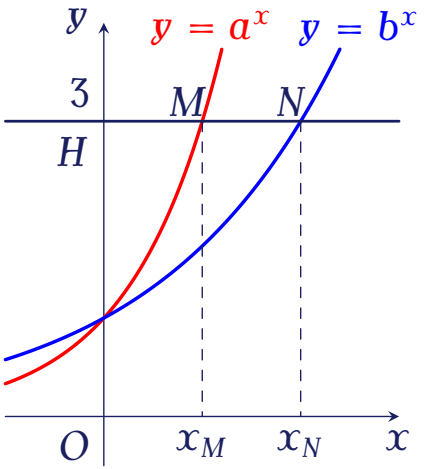
Đường thẳng $y=3$ cắt trục tung, đồ thị hàm số $y=a^x$, đồ thị hàm số $y=b^x$ lần lượt tại $H,\,M,\,N$. Biết rằng $HM=2MN$. Mệnh đề nào sau đây đúng?
| $a^2=b^3$ | |
| $3a=2b$ | |
| $a^3=b^2$ | |
| $2a=b$ |
Một bình đựng nước dạng hình nón (không có nắp đậy), đựng đầy nước. Biết rằng chiều cao của bình gấp $3$ lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là $\dfrac{16\pi}{9}\text{dm}^3$. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (hình vẽ).
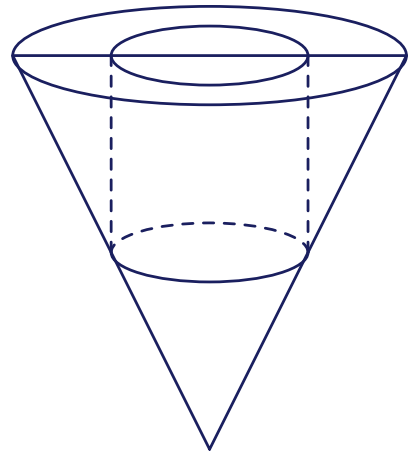
Tính bán kính đáy $R$ của bình nước.
| $R=4$dm | |
| $R=2$dm | |
| $R=3$dm | |
| $R=5$dm |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong như hình vẽ bên.
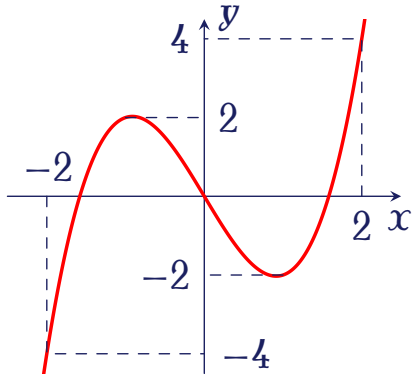
Hỏi phương trình $\big|f(x)-1\big|=1$ có bao nhiêu nghiệm?
| $6$ | |
| $3$ | |
| $4$ | |
| $5$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{0\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên.
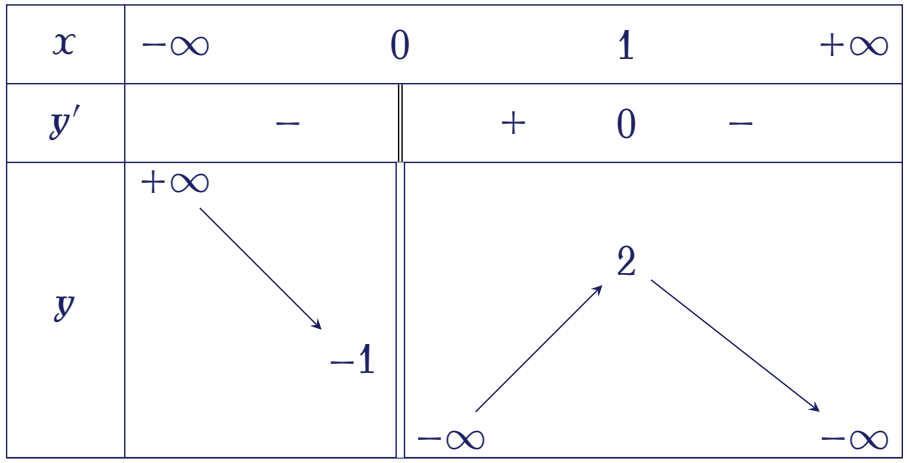
Tập hợp tất cả các giá trị của tham số $m$ sao cho phương trình $f(x)=m$ có ba nghiệm phân biệt là
| $(-\infty;2)$ | |
| $\{-1;2\}$ | |
| $[-1;2]$ | |
| $(-1;2)$ |
Có bao nhiêu giá trị nguyên thuộc đoạn $[-10;10]$ của $m$ để giá trị lớn nhất của hàm số $y=\dfrac{2x+m}{x+1}$ trên đoạn $[-4;-2]$ không lớn hơn $1$?
| $6$ | |
| $7$ | |
| $8$ | |
| $5$ |
Có bao nhiêu số nguyên $m$ để phương trình $$\log_{\sqrt{2}}\big(mx-6x^3\big)+2\log_{\tfrac{1}{2}}\big(-14x^2+29x-2\big)=0$$có nghiệm thực duy nhất.
| $18$ | |
| Vô số | |
| $22$ | |
| $23$ |
Từ một tấm tôn có kích thước $90\text{cm}\times300\text{cm}$, người ta làm một máng thoát nước, mặt cắt ngang của máng là hình thang cân $ABCD$ có đáy lớn $AD$, $AB=BC=CD=30$cm (hình minh họa bên).
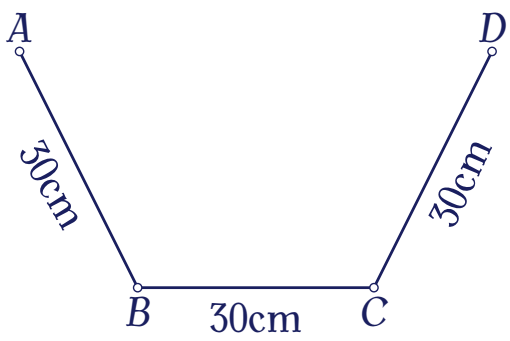
Thể tích lớn nhất của máng bằng
| $40500\sqrt{2}\text{cm}^3$ | |
| $40500\sqrt{5}\text{cm}^3$ | |
| $40500\sqrt{6}\text{cm}^3$ | |
| $202500\sqrt{3}\text{cm}^3$ |
Cho tứ diện $ABCD$, trên các cạnh $BC$, $BD$, $AC$ lần lượt lấy các điểm $M,\,N,\,P$ sao cho $BC=3BM$, $BD=\dfrac{3}{2}BN$, $AC=2AP$. Mặt phẳng $(MNP)$ chia khối tứ diện $ABCD$ thành hai khối đa diện có thể tích là $V_1$, $V_2$, trong đó khối đa diện chứa cạnh $CD$ có thể tích là $V_2$. Tính tỉ số $\dfrac{V_1}{V_2}$.
| $\dfrac{V_1}{V_2}=\dfrac{26}{19}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{26}{13}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{3}{19}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{15}{19}$ |
Cho khối hộp $ABCD.A'B'C'D'$ có thể tích bằng $6a^3$ và diện tích tam giác $A'BD$ bằng $a^2$. Khoảng cách từ điểm $A$ đến mặt phẳng $(B'CD')$ bằng
| $6a$ | |
| $2a$ | |
| $3a$ | |
| $a$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f'(x)=(x-1)^2(3-x)\big(x^2-x-1\big)$. Hỏi hàm số $f(x)$ có bao nhiêu điểm cực tiểu?
| $3$ | |
| $2$ | |
| $1$ | |
| $0$ |
Giá trị nhỏ nhất của hàm số $f(x)=x^2+\dfrac{2}{x}$ trên đoạn $\left[\dfrac{1}{2};3\right]$ bằng
| $4$ | |
| $2$ | |
| $1$ | |
| $3$ |
Đồ thị của hàm số $y=f(x)$ có dạng như đường cong trong hình vẽ bên.
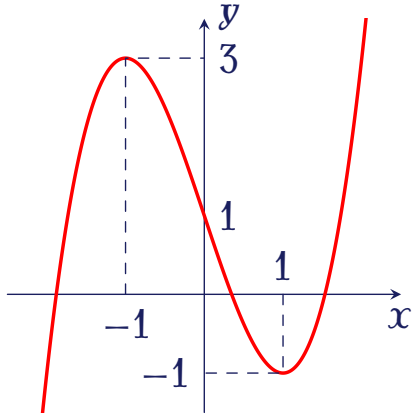
Gọi $M$ là giá trị lớn nhất, $m$ là giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $[-1;1]$. Tính $P=M-2m$.
| $P=5$ | |
| $P=3$ | |
| $P=1$ | |
| $P=4$ |
Cho khối lăng trụ có chiều cao $h$ và diện tích đáy $B$. Thể tích khối lăng trụ là
| $V=\dfrac{1}{3}Bh$ | |
| $V=Bh$ | |
| $V=3Bh$ | |
| $V=\dfrac{1}{6}Bh$ |
Khối hai mươi mặt đều có số đỉnh, số cạnh, số mặt lần lượt là
| $12;20;30$ | |
| $20;30;12$ | |
| $30;12;20$ | |
| $12;30;20$ |
Tập xác định của hàm số $y=(x+2)^{-2022}$ là
| $[-2;+\infty)$ | |
| $(-2;+\infty)$ | |
| $\mathbb{R}\setminus\{-2\}$ | |
| $\mathbb{R}$ |
Cho $a>0$ và $a\neq1$. Tìm mệnh đề đúng trong các mệnh đề sau:
| $\log_ax$ có nghĩa với $\forall x\in\mathbb{R}$ | |
| $\log_a(x\cdot y)=\log_ax\cdot\log_ay$ ($a,\,y>0$) | |
| $\log_ax^n=n\log_ax$ ($x>0$) | |
| $\log_aa=0$ |
Giá trị của $M=a^{2018\cdot\log_{a^2}2017}$ ($0< a\neq1$) bằng
| $1009^{2017}$ | |
| $2017^{2018}$ | |
| $2017^{1009}$ | |
| $2018^{2017}$ |
Cho khối chóp có diện tích đáy $B=6a^2$ và chiều cao $h=2a$. Thể tích khối chóp đã cho bằng
| $12a^3$ | |
| $6a^3$ | |
| $4a^3$ | |
| $2a^3$ |
Trong hình bên là đồ thị các hàm số $y=a^x$ và $y=b^x$.
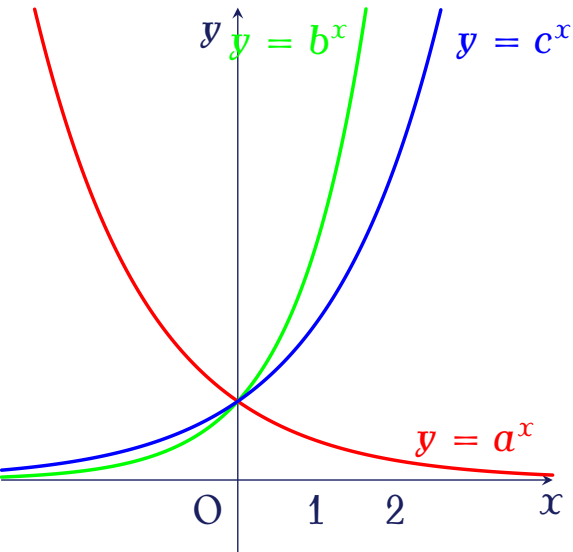
Mệnh đề nào dưới đây là đúng?
| $0< a< 1< b$ | |
| $1< a< b$ | |
| $0< a< b< 1$ | |
| $0< b< 1< a$ |
Tính đạo hàm của hàm số $y=2x^3+x\ln x$ tại điểm $x=1$.
| $6$ | |
| $2$ | |
| $3$ | |
| $7$ |
