Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\). Biết \(\cos2x\) là một nguyên hàm của hàm số \(f(x)\cdot\mathrm{e}^x\), họ tất cả các nguyên hàm của hàm số \(f'(x)\mathrm{e}^x\) là

	\(-\sin2x+\cos2x+C\)
	\(-2\sin2x+\cos2x+C\)
	\(-2\sin2x-\cos2x+C\)
	\(2\sin2x-\cos2x+C\)

Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(f(x)=\left|x^3-3x+m\right|\) trên đoạn \(\left[0;3\right]\) bằng \(16\). Tổng tất cả các phần tử của \(S\) bằng

	\(-16\)
	\(16\)
	\(-12\)
	\(-2\)

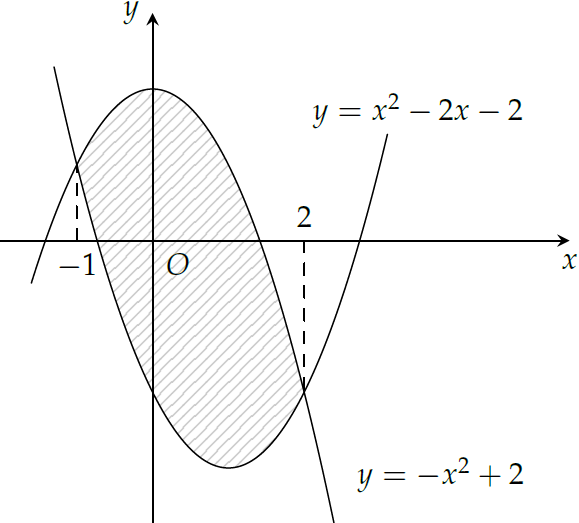
Diện tích phần hình phẳng được gạch chéo trong hình bên bằng

	\(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2+2x+4\right)\mathrm{\,d}x}\)
	\(\displaystyle\int\limits_{-1}^{2}{\left(2x^2-2x-4\right)\mathrm{\,d}x}\)
	\(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2-2x+4\right)\mathrm{\,d}x}\)
	\(\displaystyle\int\limits_{-1}^{2}{\left(2x^2+2x-4\right)\mathrm{\,d}x}\)

Cho hàm số \(f\left(x\right)\) có \(f\left(3\right)=3\) và \(f'\left(x\right)=\dfrac{x}{x+1-\sqrt{x+1}}\), \(\forall x>0\). Khi đó \(\displaystyle\int\limits_3^8f\left(x\right)\mathrm{\,d}x\) bằng

	\(7\)
	\(\dfrac{197}{6}\)
	\(\dfrac{29}{2}\)
	\(\dfrac{181}{6}\)

Nếu \(\displaystyle\int\limits_1^2f(x)\mathrm{\,d}x=-2\) và \(\displaystyle\int\limits_2^3f(x)\mathrm{\,d}x=1\) thì \(\displaystyle\int\limits_1^3f(x)\mathrm{\,d}x\) bằng

	\(-3\)
	\(-1\)
	\(1\)
	\(3\)

Họ tất cả các nguyên hàm của hàm số \(f\left(x\right)=\dfrac{x+2}{x-1}\) trên khoảng \(\left(1;+\infty\right)\) là

	\(x+3\ln\left(x-1\right)+C\)
	\(x-3\ln\left(x-1\right)+C\)
	\(x+\dfrac{3}{\left(x-1\right)^2}+C\)
	\(x-\dfrac{3}{\left(x-1\right)^2}+C\)

Họ tất cả các nguyên hàm của hàm số \(f(x)=\cos x+6x\) là

	\(\sin x+3x^2+C\)
	\(-\sin x+3x^2+C\)
	\(\sin x+6x^2+C\)
	\(-\sin x+C\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

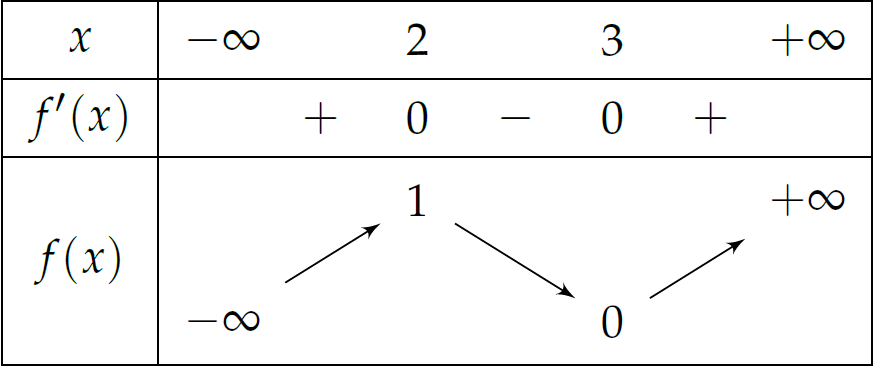
Số nghiệm thực của phương trình \(3f\left(x\right)-2=0\) là

	\(2\)
	\(0\)
	\(3\)
	\(1\)

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{5x^2-4x-1}{x^2-1}\) là

	\(1\)
	\(0\)
	\(2\)
	\(3\)

Giá trị lớn nhất của hàm số \(f\left(x\right)=-x^4+12x^2+1\) trên đoạn \(\left[-1;2\right]\) bằng

	\(1\)
	\(37\)
	\(33\)
	\(12\)

Cho hàm số \(f\left(x\right)\), bảng xét dấu của \(f'\left(x\right)\) như sau:

Số điểm cực trị của hàm số đã cho là

	\(0\)
	\(2\)
	\(1\)
	\(3\)

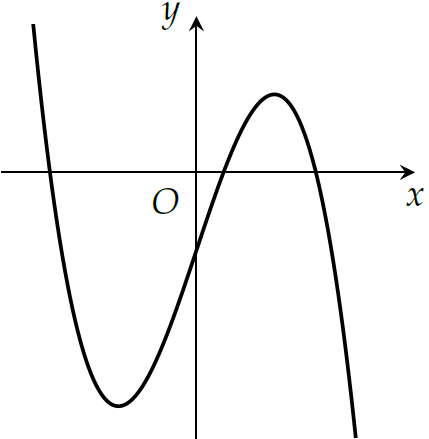
Cho hàm số \(y=ax^3+3x+d\) (\(a,\,d\in\mathbb{R}\)) có đồ thị như hình trên. Mệnh đề nào dưới đây đúng?

	\(a>0;\,d>0\)
	\(a<0;\,d>0\)
	\(a>0;\,d<0\)
	\(a<0;\,d<0\)

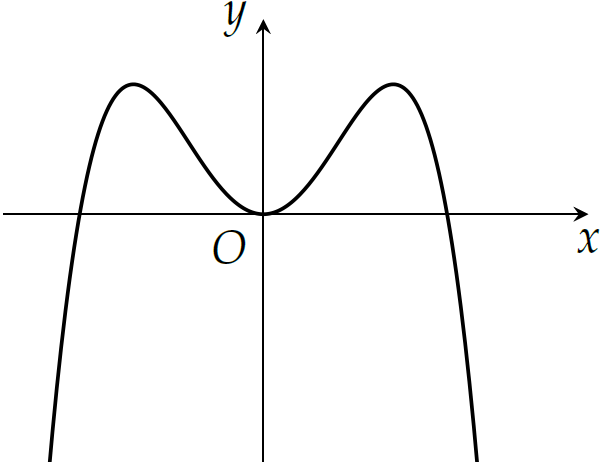
Đồ thị của hàm số nào sau đây có dạng như hình cong trong hình bên?

	\(y=-x^4+2x^2\)
	\(y=x^4-2x^2\)
	\(y=x^3-3x^2\)
	\(y=-x^3+3x^2\)

Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:

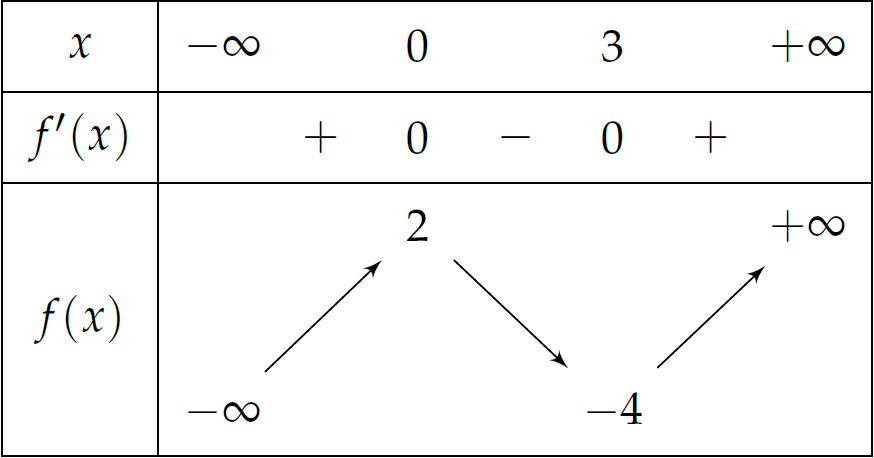
Giá trị cực tiểu của hàm số đã cho bằng

	\(2\)
	\(3\)
	\(0\)
	\(-4\)

Cho hàm số \(f\left(x\right)=\dfrac{mx-4}{x-m}\) (\(m\) là tham số thực). Có bao nhiêu giá trị nguyên của \(m\) để hàm số đồng biến trên khoảng \(\left(0;+\infty\right)\)?

	\(5\)
	\(4\)
	\(3\)
	\(2\)

Cho hàm số \(f(x)\) có bảng biến thiên như sau:

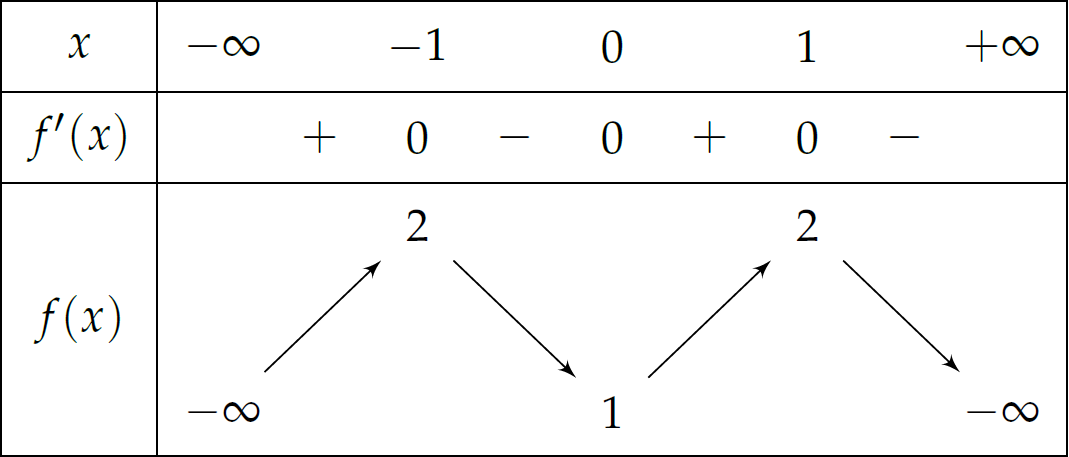
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

	\(\left(1;+\infty\right)\)
	\(\left(-1;0\right)\)
	\(\left(-1;1\right)\)
	\(\left(0;1\right)\)

Tìm tọa độ giao điểm của parabol \(y=-x^2+2x+1\) với đường thẳng \(y=2x-3\).

	\((2;1)\)
	\((2;-2)\) và \((1;-7)\)
	\((2;1)\) và \((-2;-7)\)
	\((-2;-7)\)

Đồ thị của hàm số \(y=x^2+4x+1\) là đường cong nào dưới đây?

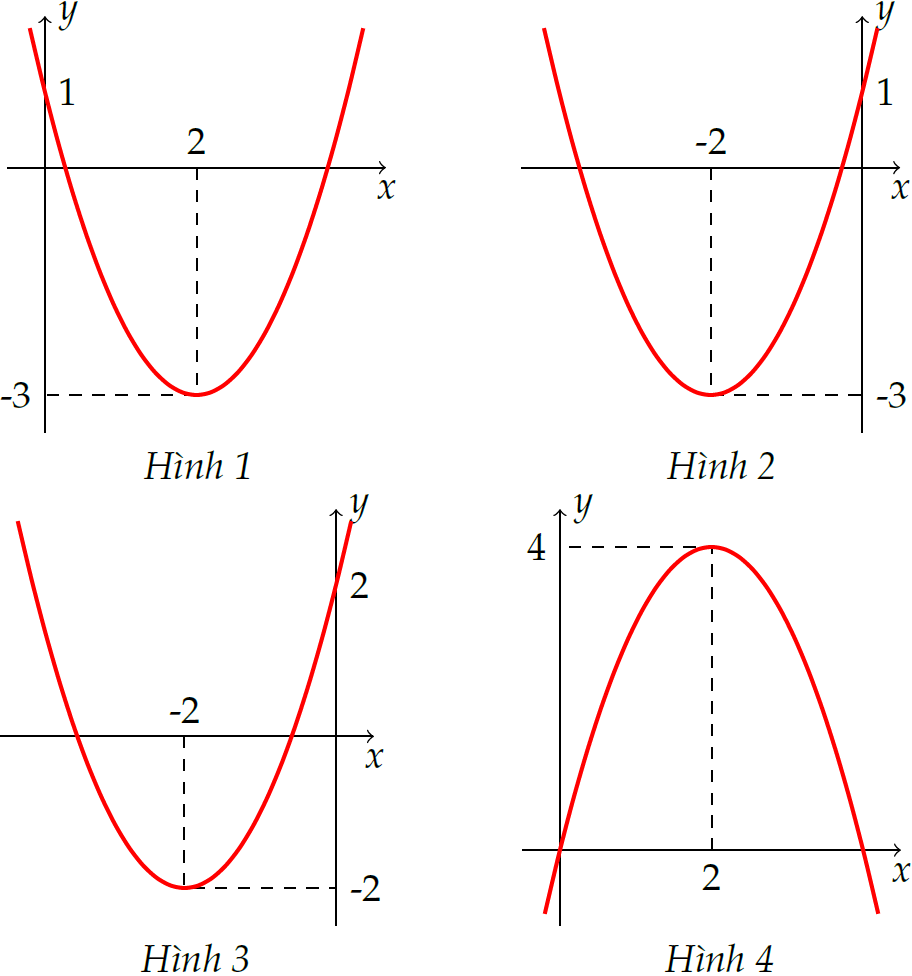
	Hình 1
	Hình 2
	Hình 3
	Hình 4

Hình vẽ sau đây là đồ thị của hàm số nào?

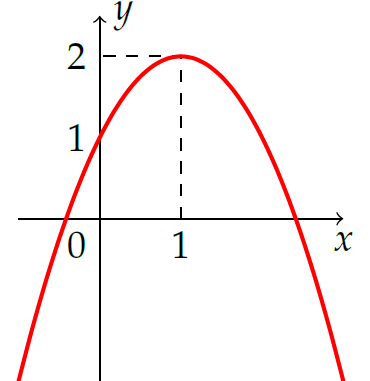
	\(y=-x^2+2x\)
	\(y=x^2-2x+1\)
	\(y=-x^2-2x+1\)
	\(y=-x^2+2x+1\)

Hàm số \(y=x^2+4x+1\) đồng biến trên khoảng

	\((-\infty;-2)\)
	\((-2;+\infty)\)
	\((2;+\infty)\)
	\((-\infty;+\infty)\)