Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\dfrac{1-x}{x+1}\) trên \([-3;-2]\) lần lượt bằng

	\(2\) và \(-3\)
	\(-3\) và \(2\)
	\(3\) và \(-2\)
	\(-2\) và \(-3\)

Số giá trị nguyên của tham số \(m\) để hàm số $$y=x^3-(m+2)x^2+\left(m^2+2m\right)x$$có cực trị là

	\(2\)
	\(1\)
	\(3\)
	\(0\)

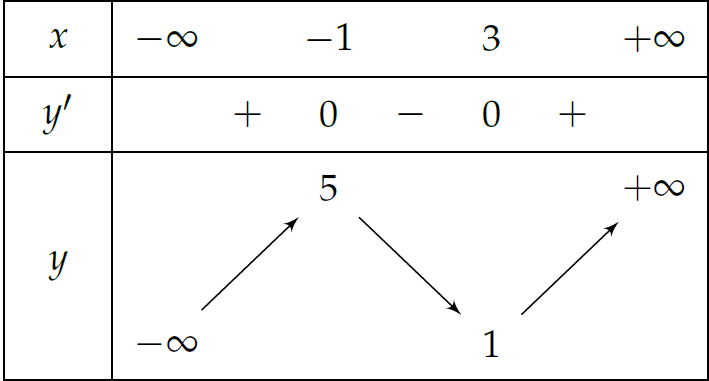
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình trên. Số điểm cực trị của hàm số \(y=\left|f(x-2)-3\right|\) bằng

	\(5\)
	\(4\)
	\(6\)
	\(3\)

Hàm số \(y=x^3+mx^2\) đạt cực đại tại \(x=-2\) khi và chỉ khi giá trị của tham số thực \(m\) bằng

	\(-3\)
	\(3\)
	\(-12\)
	\(12\)

Số điểm cực trị của hàm số \(f(x)\) có đạo hàm \(f'(x)=x(x-1)^2\), \(\forall x\in\mathbb{R}\) là

	\(1\)
	\(2\)
	\(3\)
	\(4\)

Số điểm cực trị của hai hàm số \(y=x^4\) và \(y=\mathrm{e}^x\) lần lượt bằng

	\(0\) và \(0\)
	\(0\) và \(1\)
	\(1\) và \(1\)
	\(1\) và \(0\)

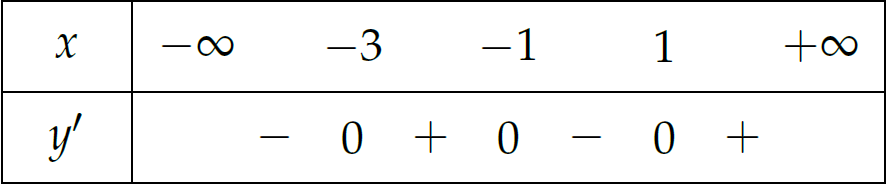
Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu như hình bên. Hàm số \(f(3-2x)\) đồng biến trên khoảng nào dưới đây?

	\((3;4)\)
	\((2;3)\)
	\((0;2)\)
	\((-\infty;-3)\)

Tập hợp các tham số thực \(m\) để hàm số \(y=\dfrac{x}{x-m}\) nghịch biến trên \((1;+\infty)\) là

	\((0;1)\)
	\([0;1)\)
	\((0;1]\)
	\([0;1]\)

Tập hợp các tham số thực \(m\) để hàm số \(y=x^3-3mx^2+3x\) đồng biến trên \((1;+\infty)\) là

	\((-\infty;0]\)
	\((-\infty;1]\)
	\((-\infty;2)\)
	\((-\infty;1)\)

Số giá trị nguyên của tham số \(m\) để hàm số \(y=x^3-mx^2-2mx\) đồng biến trên \(\mathbb{R}\) là

	\(0\)
	\(8\)
	\(7\)
	\(6\)

Hàm số nào dưới đây đồng biến trên \((-\infty;+\infty)\)?

	\(y=\dfrac{x-1}{x}\)
	\(y=2x^3\)
	\(y=x^2+1\)
	\(y=x^4+5\)

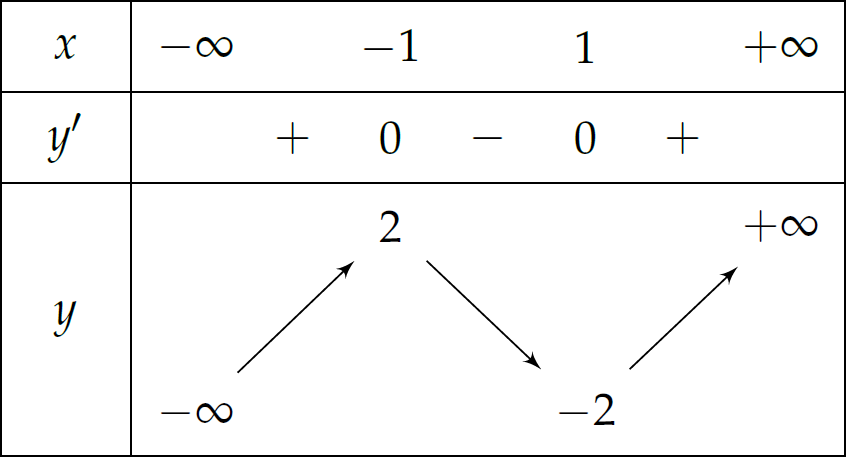
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình trên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

	\((-1;1)\)
	\((-2;2)\)
	\((1;+\infty)\)
	\((-\infty;1)\)

Hàm số \(y=\sqrt{x^4+1}\) có đạo hàm \(y'\) bằng

	\(\dfrac{1}{\sqrt{x^4+1}}\)
	\(\dfrac{4x^3}{\sqrt{x^4+1}}\)
	\(\dfrac{2x^3}{\sqrt{x^4+1}}\)
	\(\dfrac{x^4}{2\sqrt{x^4+1}}\)

Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\dfrac{3-x}{\sqrt{4-3x-x^2}}$$

	\(\mathscr{D}=\mathbb{R}\setminus\{-4;1\}\)
	\(\mathscr{D}=[-4;1]\)
	\(\mathscr{D}=(-4;1)\)
	\(\mathscr{D}=(-\infty;4)\cup(1;+\infty)\)

Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\sqrt{2x^2-5x+2}$$

	\(\mathscr{D}=\left(-\infty;\dfrac{1}{2}\right]\)
	\(\mathscr{D}=\left[2;+\infty\right)\)
	\(\mathscr{D}=\left(-\infty;\dfrac{1}{2}\right]\cup[2;+\infty)\)
	\(\mathscr{D}=\left[\dfrac{1}{2};2\right]\)

Tính thể tích khối tròn xoay được tạo bởi hình phẳng giới hạn bởi ba đường \(y=\sqrt{x}\), \(y=2-x\) và \(y=0\) quanh trục \(Ox\).

	\(\dfrac{3\pi}{2}\)
	\(\dfrac{5\pi}{6}\)
	\(\pi\)
	\(\dfrac{2\pi}{3}\)

Cho hình phẳng giới hạn bởi đồ thị hàm số \(y=\mathrm{e}^x\), trục \(Ox\), hai đường thẳng \(x=0\), \(x=1\). Thể tích khối tròn xoay khi quay hình đó xung quanh trục hoành được cho bởi công thức

	\(\left(\pi\displaystyle\int\limits_{0}^{1}\mathrm{e}^x\mathrm{\,d}x\right)^2\)
	\(\pi\displaystyle\int\limits_{0}^{1}\mathrm{e}^{2x}\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{0}^{1}\mathrm{e}^{2x}\mathrm{\,d}x\)
	\(\pi\left(\displaystyle\int\limits_{0}^{1}\mathrm{e}^x\mathrm{\,d}x\right)^2\)

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng \(D\) giới hạn bởi các đường \(y=\sqrt{x-1}\), trục hoành, \(x=2\) và \(x=5\) quanh trục \(Ox\) bằng

	\(\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{2}^{5}\sqrt{x-1}\mathrm{\,d}x\)
	\(\pi\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x\)
	\(\pi^2\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x\)

Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y=x^2\) và \(y=x\) là

	\(1\)
	\(\dfrac{3}{2}\)
	\(\dfrac{1}{2}\)
	\(\dfrac{1}{6}\)

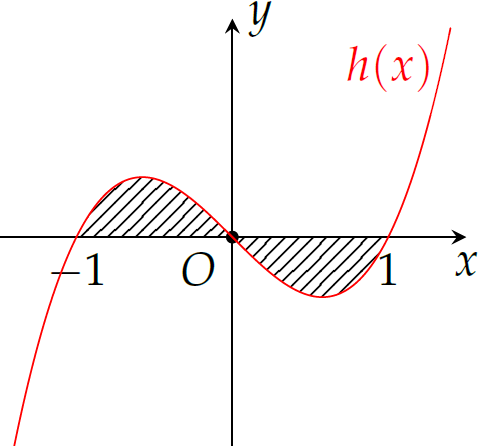
Cho đồ thị hàm số \(y=h(x)\). Diện tích hình phẳng (phần gạch chéo trong hình vẽ) bằng

	\(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{-1}^{1}h(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{0}h(x)\mathrm{\,d}x\)
	\(-\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\)