Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=-x^4+6x^2+mx$ có ba điểm cực trị?
| $17$ | |
| $15$ | |
| $3$ | |
| $7$ |
Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-2)^2(1-x)$ với mọi $x\in\mathbb{R}$. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
| $(1;2)$ | |
| $(1;+\infty)$ | |
| $(2;+\infty)$ | |
| $(-\infty;1)$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
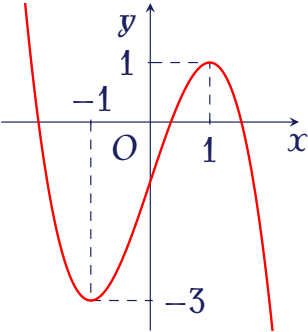
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(x)=m$ có ba nghiệm thực phân biệt?
| $2$ | |
| $5$ | |
| $3$ | |
| $4$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
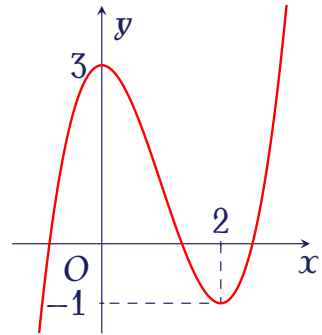
Giá trị cực đại của hàm số đã cho là
| $-1$ | |
| $3$ | |
| $2$ | |
| $0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(0;2)$ | |
| $(3;+\infty)$ | |
| $(-\infty;1)$ | |
| $(1;3)$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x+1}{3x-1}$ là đường thẳng có phương trình
| $y=\dfrac{1}{3}$ | |
| $y=-\dfrac{2}{3}$ | |
| $y=-\dfrac{1}{3}$ | |
| $y=\dfrac{2}{3}$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
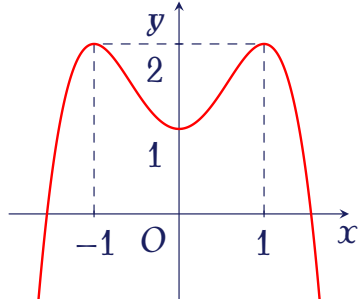
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
| $(-1;2)$ | |
| $(0;1)$ | |
| $(1;2)$ | |
| $(1;0)$ |
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
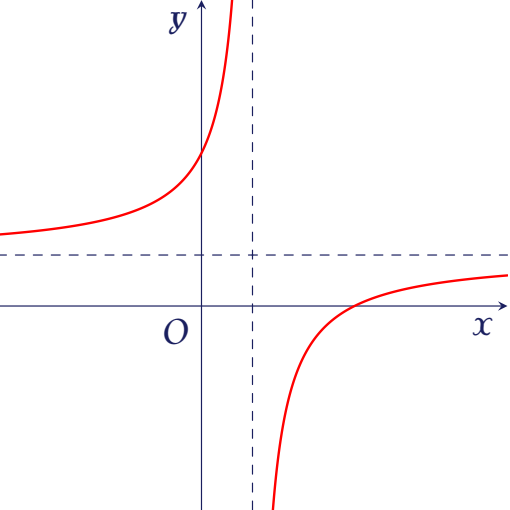
| $y=x^4-3x^2+2$ | |
| $y=\dfrac{x-3}{x-1}$ | |
| $y=x^2-4x+1$ | |
| $y=x^3-3x-5$ |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình bên.
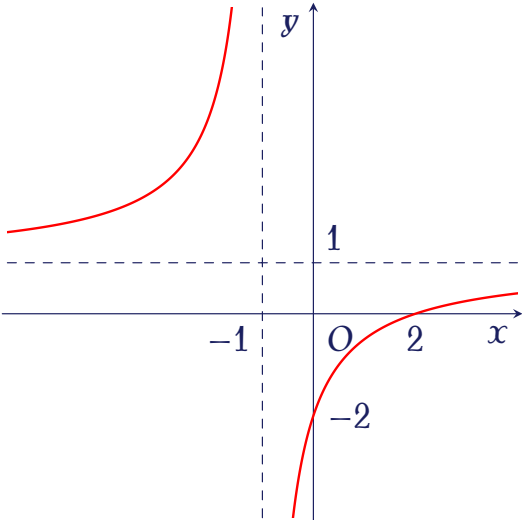
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
| $(0;-2)$ | |
| $(2;0)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=x^{\pi}$ là
| $y'=\pi x^{\pi-1}$ | |
| $y'=x^{\pi-1}$ | |
| $y'=\dfrac{1}{\pi}x^{\pi-1}$ | |
| $y'=\pi x^{\pi}$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=\log_3x$ là
| $y'=\dfrac{1}{x}$ | |
| $y'=\dfrac{1}{x\ln3}$ | |
| $y'=\dfrac{\ln3}{x}$ | |
| $y'=-\dfrac{1}{x\ln3}$ |
Một mảnh vườn hình elip có độ dài trục lớn $8$m và độ dài trục nhỏ $6$m. Người ta cần trồng rau trên dải đất rộng $4$m như hình vẽ.
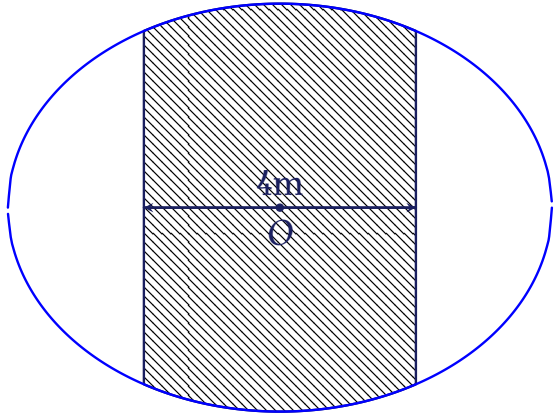
Hỏi cần bao nhiêu tiền để trồng rau trên dải đất đó, biết rằng kinh phí trồng rau là $70000$ đồng/m$^2$?
| $1.607.107$ đồng | |
| $803.553$ đồng | |
| $267.851$ đồng | |
| $2.638.938$ đồng |
Tiệm cận ngang của đồ thị hàm số $y=3^x$ và tiệm cận đứng của đồ thị hàm số $y=\log_2x$ lần lượt có phương trình là
| $y=3$ và $x=0$ | |
| $x=0$ và $y=0$ | |
| $y=0$ và $x=2$ | |
| $y=0$ và $x=0$ |
Tính tích phân $\displaystyle\int\limits_{1}^{2}\left(x^2+4x+\dfrac{4}{x^2}\right)\mathrm{\,d}x$.
Tính tích phân $\displaystyle\int\limits_{0}^{1}(2x+1)^5\mathrm{\,d}x$.
Tính tích phân $I=\displaystyle\int\limits_{0}^{1}x(1+x)^2\mathrm{\,d}x$.
Cho $\lim\limits_{x\to x_0^+}f(x)=5$, $\lim\limits_{x\to x_0^-}f(x)=-5$. Chọn khẳng định đúng.
| $\lim\limits_{x\to x_0}f(x)=\pm5$ | |
| $\lim\limits_{x\to x_0}f(x)=5$ | |
| $\lim\limits_{x\to x_0}f(x)=-5$ | |
| Không tồn tại $\lim\limits_{x\to x_0}f(x)$ |
Hàm số $f(x)$ được gọi là liên tục trên khoảng $(a;b)$ nếu
| $f(x)$ liên tục tại $2$ điểm thuộc khoảng $(a;b)$ | |
| $f(x)$ liên tục tại mọi điểm thuộc khoảng $(a;b)$ | |
| $f(x)$ liên tục tại $4$ điểm thuộc khoảng $(a;b)$ | |
| $f(x)$ liên tục tại $a$ và liên tục tại $b$ |
Cho hàm số $f(x)=\dfrac{2x+3}{(x-1)(x-2)}$. Chọn khẳng định đúng.
| $f(x)$ không liên tục tại $x_0=3$ | |
| $f(x)$ liên tục tại $x_0=3$ | |
| $f(x)$ liên tục tại $x_0=1$ | |
| $f(x)$ liên tục tại $x_0=2$ |
