Cho hai số phức \(z_1=2+3i\), \(z_2=4+5i\). Số phức liên hợp của số phức \(w=2\left(z_1+z_2\right)\) là

	\(\overline{w}=28i\)
	\(\overline{w}=12+8i\)
	\(\overline{w}=8+10i\)
	\(\overline{w}=12-16i\)

Cho hai số phức \(z_1=2-2i\), \(z_2=-3+3i\). Khi đó số phức \(z_1-z_2\) là

	\(-1+i\)
	\(-5+5i\)
	\(5-5i\)
	\(-5i\)

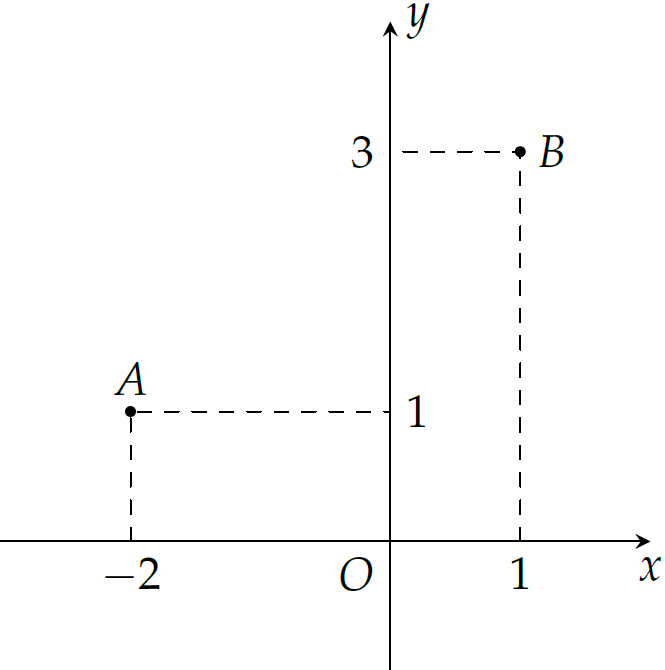
Trong mặt phẳng \(Oxy\), cho các điểm \(A,\,B\) như hình vẽ trên. Trung điểm của đoạn thẳng \(AB\) biểu diễn số phức

	\(-\dfrac{1}{2}+2i\)
	\(2-\dfrac{1}{2}i\)
	\(-1+2i\)
	\(2-i\)

Số phức \(-3+7i\) có phần ảo bằng

	\(-7\)
	\(-3\)
	\(3\)
	\(7\)

Tìm tập nghiệm \(S\) của phương trình \(z^4-7z^2-18=0\) trên tập số phức.

	\(S=\left\{-2;9\right\}\)
	\(S=\left\{-\sqrt{2};\sqrt{2};-3i;3i\right\}\)
	\(S=\left\{-4i;4i;-81;81\right\}\)
	\(S=\left\{-3;3;-\sqrt{2}i;\sqrt{2}i\right\}\)

Kí hiệu \(z_0\) là nghiệm phức có phần ảo dương của phương trình \(2z^2-6z+15=0\). Trên mặt phẳng tọa độ, tìm tọa độ của điểm \(M\) biểu diễn số phức \(z_0\).

	\(M\left(-\dfrac{3}{2};\dfrac{\sqrt{21}}{2}i\right)\)
	\(M\left(-\dfrac{3}{2};\dfrac{\sqrt{21}}{2}\right)\)
	\(M\left(\dfrac{3}{2};\dfrac{\sqrt{21}}{2}\right)\)
	\(M\left(\dfrac{3}{2};\dfrac{\sqrt{21}}{2}i\right)\)

Tìm nghiệm phức có phần ảo âm của phương trình $$z^2-4z+13=0.$$

	\(z=-2-3i\)
	\(z=2-3i\)
	\(z=-2+3i\)
	\(z=2+3i\)

Tìm một căn bậc hai của \(-8\).

	\(-2\sqrt{2}i\)
	\(-2\sqrt{2}\)
	\(2\sqrt{2}\)
	\(2\sqrt{-2}i\)

Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện \(|z-2+3i|=4\).

	Đường tròn tâm \(I(2;-3)\) và bán kính \(R=4\)
	Đường tròn tâm \(I(-2;3)\) và bán kính \(R=16\)
	Đường tròn tâm \(I(-2;3)\) và bán kính \(R=4\)
	Đường tròn tâm \(I(2;-3)\) và bán kính \(R=16\)

Tìm số phức \(z\) thỏa mãn $$z-1+4i=2i\overline{z}.$$

	\(z=\dfrac{9}{5}-\dfrac{2}{5}i\)
	\(z=-\dfrac{9}{5}+\dfrac{2}{5}i\)
	\(z=\dfrac{7}{3}+\dfrac{2}{3}i\)
	\(z=-\dfrac{7}{3}-\dfrac{2}{3}i\)

Tìm số phức \(z\) thỏa mãn $$(3-5i)z+(2+3i)=-4i.$$

	\(z=\dfrac{2}{17}-\dfrac{8}{17}i\)
	\(z=\dfrac{29}{34}-\dfrac{31}{34}i\)
	\(z=\dfrac{1}{17}-\dfrac{21}{17}i\)
	\(z=-\dfrac{1}{34}-\dfrac{13}{34}i\)

Tìm số phức liên hợp của số phức $$z=(11-3i)+(5+2i)(1-i).$$

	\(\overline{z}=14+6i\)
	\(\overline{z}=18+6i\)
	\(\overline{z}=18-6i\)
	\(\overline{z}=14-6i\)

Tìm phần thực và phần ảo của số phức $$z=\dfrac{6-3i}{2+5i}.$$

	Phần thực là \(-\dfrac{3}{29}\) và phần ảo là \(-\dfrac{36}{29}\)
	Phần thực là \(-\dfrac{3}{29}\) và phần ảo là \(-\dfrac{36}{29}i\)
	Phần thực là \(\dfrac{1}{7}\) và phần ảo là \(\dfrac{12}{7}\)
	Phần thực là \(\dfrac{1}{7}\) và phần ảo là \(\dfrac{12}{7}i\)

Tính môđun của số phức $$z=\dfrac{\left(-2-3i\right)\left(-1+2i\right)}{2+i}.$$

	\(|z|=\sqrt{13}\)
	\(|z|=\sqrt{5}\)
	\(|z|=13\)
	\(|z|=5\)

Cho hai số phức \(z_1=\dfrac{1}{2}-2i\) và \(z_2=4-i\). Tính môđun của số phức \(z=z_1\cdot z_2\).

	\(|z|=\dfrac{\sqrt{34}}{2}\)
	\(|z|=\dfrac{289}{4}\)
	\(|z|=\dfrac{17}{2}\)
	\(|z|=-\dfrac{17}{2}\)

Cho hai số phức \(z_1=-4+\sqrt{2}i\) và \(z_2=1-\sqrt{3}i\). Tìm phần ảo của số phức \(z_1-z_2\).

	Phần ảo là \(\sqrt{5}\)
	Phần ảo là \(\sqrt{2}-\sqrt{3}\)
	Phần ảo là \(\sqrt{2}+\sqrt{3}\)
	Phần ảo là \(-5\)

Cho hai số phức \(z_1=3+2i\) và \(z_2=1-5i\). Tìm phần thực và phần ảo của số phức \(z_1+z_2\).

	Phần thực là \(4\) và phần ảo là \(3\)
	Phần thực là \(4\) và phần ảo là \(-3i\)
	Phần thực là \(4\) và phần ảo là \(3i\)
	Phần thực là \(4\) và phần ảo là \(-3\)

Cho số phức \(z=(2m-1)+(m^2-4)i\), \(m\in\mathbb{R}\). Tìm \(m\) để số phức \(z\) là số thuần ảo.

	\(m=2,\,m=-2\)
	\(m=2\)
	\(m=-\dfrac{1}{2}\)
	\(m=\dfrac{1}{2}\)

Trên mặt phẳng tọa độ, tìm tọa độ của điểm \(M\) biểu diễn số phức \(z=5-i\).

	\(M(5;0)\)
	\(M(5;-1)\)
	\(M(0;-5)\)
	\(M(5;1)\)

Tìm phần thực và phần ảo của số phức \(z=2-3i\).

	Phần thực là \(2\) và phần ảo là \(3\)
	Phần thực là \(2\) và phần ảo là \(-3\)
	Phần thực là \(2\) và phần ảo là \(3i\)
	Phần thực là \(2\) và phần ảo là \(-3i\)