Cho hàm số bậc ba \(y=f(x)\) có đồ thị là đường cong trong hình.

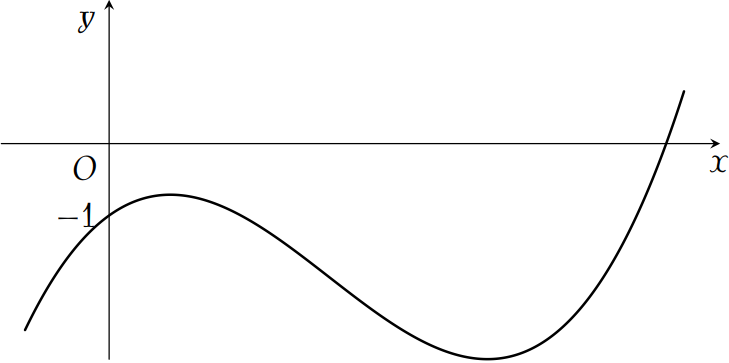
Số nghiệm thực phân biệt của phương trình \(f\left(x^3f(x)\right)+1=0\) là

	\(8\)
	\(5\)
	\(6\)
	\(4\)

Cho hàm số \(y=ax^3+bx^2+cx+d\) (\(a,\,b,\,c,\,d\in\mathbb{R}\)) có đồ thị là đường cong trong hình.

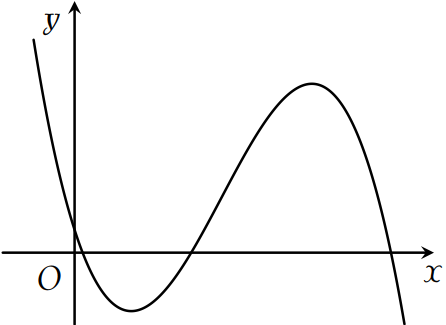
Có bao nhiêu số dương trong các số \(a\), \(b\), \(c\), \(d\)?

	\(4\)
	\(1\)
	\(2\)
	\(3\)

Số giao điểm của đồ thị hàm số \(y=x^3+3x^2\) và đồ thị hàm số \(y=3x^2+3x\) là

	\(3\)
	\(1\)
	\(2\)
	\(0\)

Cho hàm số bậc ba \(y=f\left(x\right)\) có đồ thị là đường cong trong hình.

Số nghiệm thực của phương trình \(f\left(x\right)=-1\) là

	\(3\)
	\(1\)
	\(0\)
	\(2\)

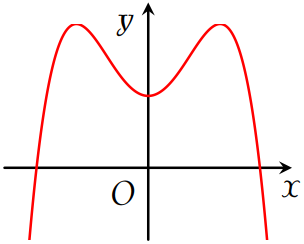
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình trên?

	\(y=x^3-3x^2+1\)
	\(y=-x^3+3x^2+1\)
	\(y=-x^4+2x^2+1\)
	\(y=x^4-2x^2+1\)

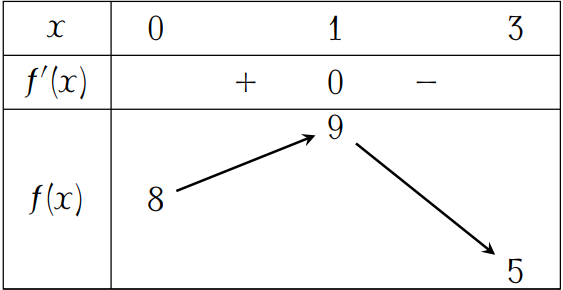
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là

	\(9\)
	\(10\)
	Vô số
	\(0\)

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \((-6;5)\) sao cho phương trình $$2\cos2x+4\sin x-m\sqrt{2}=0$$vô nghiệm?

	\(3\)
	\(2\)
	\(4\)
	\(5\)

Tìm \(m\) để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\).

	\(m\leq3\)
	\(m\leq-3\)
	\(m\leq5\)
	\(m\leq-1\)

Tiếp tuyến của đường cong \(\left(\mathscr{C}\right)\colon y=\dfrac{2x+1}{x-1}\) tại điểm \(M(2;5)\) cắt các trục tọa độ \(Ox\), \(Oy\) lần lượt tại \(A\) và \(B\). Tính diện tích tam giác \(OAB\).

	\(\dfrac{121}{6}\)
	\(\dfrac{121}{3}\)
	\(-\dfrac{121}{6}\)
	\(-\dfrac{121}{3}\)

Biết rằng tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số $$y=\dfrac{1}{3}x^3-(m-1)x^2-(m-3)x+2020m$$đồng biến trên khoảng \((-3;-1)\) và \((0;3)\) là đoạn \(T=[a;b]\). Tính \(a^2+b^2\).

	\(a^2+b^2=8\)
	\(a^2+b^2=13\)
	\(a^2+b^2=10\)
	\(a^2+b^2=5\)

Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y=x+\dfrac{4}{x}\) trên khoảng \((0;+\infty)\). Tìm \(m\).

	\(m=2\)
	\(m=3\)
	\(m=1\)
	\(m=4\)

Tìm tất cả giá trị của tham số \(m\) để hàm số $$y=x^3+2x^2-mx+1$$đồng biến trên \(\mathbb{R}\).

	\(m\leq-\dfrac{4}{3}\)
	\(m\geq-\dfrac{4}{3}\)
	\(m<-\dfrac{4}{3}\)
	\(m>-\dfrac{4}{3}\)

Tập hợp các giá trị \(m\) để đồ thị hàm số \(y=\dfrac{mx^2+6x-2}{x+2}\) có tiệm cận đứng là

	\(\left\{\dfrac{7}{2}\right\}\)
	\(\mathbb{R}\setminus\left\{-\dfrac{7}{2}\right\}\)
	\(\mathbb{R}\)
	\(\mathbb{R}\setminus\left\{\dfrac{7}{2}\right\}\)

Điểm cực tiểu của đồ thị hàm số \(y=-x^3+x^2+5x-5\) là điểm nào?

	\((-1;-8)\)
	\((1;0)\)
	\((0;-5)\)
	\(\left(\dfrac{5}{3};\dfrac{40}{27}\right)\)

Đồ thị sau đây là của hàm số \(y=x^3-3x+1\).

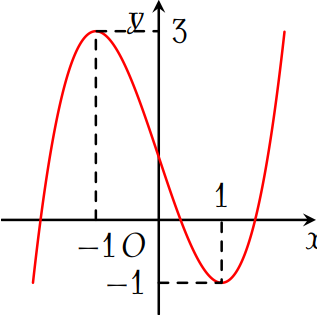
Với giá trị nào của \(m\) thì phương trình \(x^3-3x-m=0\) có \(3\) nghiệm phân biệt?

	\(-2< m<2\)
	\(-2< m<3\)
	\(-1< m<3\)
	\(-2\leq m<2\)

Cho hàm số \(y=f(x)\) có đạo hàm trên khoảng \(\mathbb{K}\). Mệnh đề nào dưới đây đúng?

	Nếu \(f'(x)\geq0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)\leq0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)<0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)
	Nếu \(f'(x)>0\) với mọi \(x\) thuộc \(\mathbb{K}\) thì hàm số \(f(x)\) đồng biến trên \(\mathbb{K}\)

Biết rằng đường thẳng \(y=4x+5\) cắt đồ thị hàm số \(y=x^3+2x+1\) tại điểm duy nhất, kí hiệu \(\left(x_0;y_0\right)\) là tọa độ của điểm đó. Tìm \(y_0\).

	\(y_0=11\)
	\(y_0=10\)
	\(y_0=13\)
	\(y_0=12\)

Hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có bảng biến thiên như sau:

Gọi \(M\) là giá trị lớn nhất của hàm số \(y=f(x)\) trên đoạn \([-1;3]\). Khẳng định nào sau đây là khẳng định đúng?

	\(M=f(0)\)
	\(M=f(3)\)
	\(M=f(2)\)
	\(M=f(-1)\)

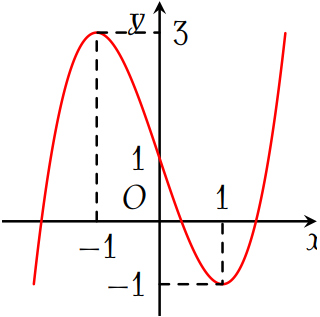
Đường cong trong hình vẽ là đồ của hàm số nào dưới đây?

	\(y=x^3-3x+3\)
	\(y=x^3-3x\)
	\(y=x^3-3x+1\)
	\(y=-x^3+3x+1\)

Hàm số nào sau đây không có điểm cực trị?

	\(y=-x^4+2x^2-5\)
	\(y=x^4+2x^2-5\)
	\(y=-\dfrac{1}{4}x^4+6\)
	\(y=x^3+6x-2019\)