Cho hàm số \(f(x)\)  liên tục trên đoạn \([a;b]\) và \(F(x)\) là một nguyên hàm của \(f(x)\) trên đoạn \([a;b]\). Mệnh đề nào dưới đây đúng?

	\(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=F(a)-F(b)\)
	\(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=f(b)-f(a)\)
	\(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=f(a)-f(b)\)
	\(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=F(b)-F(a)\)

Cho \(I=\displaystyle\int\limits_0^4x\sqrt{1+2x}\mathrm{\,d}x\) và \(u=\sqrt{2x+1}\). Mệnh đề nào sau đây sai?

	\(I=\dfrac{1}{2}\left(\dfrac{u^5}{5}-\dfrac{u^3}{3}\right)\bigg|_1^3\)
	\(I=\displaystyle\int\limits_1^3u^2\left(u^2-1\right)\mathrm{\,d}u\)
	\(I=\dfrac{1}{2}\displaystyle\int\limits_1^3x^2\left(x^2-1\right)\mathrm{\,d}x\)
	\(I=\dfrac{1}{2}\displaystyle\int\limits_1^3u^2\left(u^2-1\right)\mathrm{\,d}u\)

Cho tích phân \(I=\displaystyle\int_0^4x\sqrt{x^2+9}\mathrm{\,d}x\). Khi đặt \(t=\sqrt{x^2+9}\) thì tích phân đã cho trở thành

	\(I=\displaystyle\int_3^5t\mathrm{\,d}t\)
	\(I=\displaystyle\int_0^4t\mathrm{\,d}t\)
	\(I=\displaystyle\int_0^4t^2\mathrm{\,d}t\)
	\(I=\displaystyle\int_3^5t^2\mathrm{\,d}t\)

Cho \(\displaystyle\int\limits_1^3 \dfrac{\left(x+6\right)^{2017}}{x^{2019}}\mathrm{\,d}x=\dfrac{a^{2018}-3^{2018}}{6\cdot 2018}\). Tính \(a\).

	\(7\)
	\(9\)
	\(6\)
	\(8\)

Tích phân \(I=\displaystyle\int\limits_0^1\dfrac{\left(x-1\right)^2}{x^2+1}\mathrm{\,d}x=a-\ln b\), trong đó \(a,\,b\) là các số nguyên. Tính giá trị của biểu thức \(a+b\).

	\(1\)
	\(0\)
	\(-1\)
	\(3\)

Biết rằng \(\displaystyle\int\limits_2^7\dfrac{x\mathrm{\,d}x}{x^2+1}=a\ln2-b\ln5\) với \(a,\,b\in\Bbb{Q}\). Giá trị của \(2a+b\) bằng

	\(\dfrac{3}{2}\)
	\(\dfrac{1}{2}\)
	\(1\)
	\(2\)

Cho hai quả bóng \(A\), \(B\) di chuyển ngược chiều và va chạm với nhau. Sau va chạm, mỗi quả bóng nảy ngược lại một đoạn thì dừng hẳn. Biết sau khi va chạm, quả bóng \(A\) nảy ngược lại với vận tốc \(v_A(t)=8-2t\) (m/s) và quả bóng \(B\) nảy ngược lại với vận tốc \(v_B(t)=12-4t\) (m/s). Tính khoảng cách giữa hai quả bóng sau khi đã dừng hẳn. (Giả sử hai quả bóng đều chuyển động thẳng)

	\(36\) m
	\(32\) m
	\(34\) m
	\(30\) m

Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu \(1\) m. Một ô tô \(A\) đang chạy với vận tốc \(12\) m/s bỗng gặp ô tô \(B\) đang dừng đèn đỏ nên ô tô \(A\) hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức \(v_A(t)=12-4t\) (đơn vị tính bằng m/s), thời gian \(t\) tính bằng giây. Hỏi rằng để hai ô tô \(A\) và \(B\) đạt khoảng cách an toàn khi dừng lại thì ô tô \(A\) phải hãm phanh khi cách ô tô \(B\) một khoảng ít nhất là bao nhiêu mét?

	\(37\)
	\(17\)
	\(19\)
	\(18\)

Một chiếc xe đang chạy đều với vận tốc \(20\) m/s thì giảm phanh với vận tốc \(v(t)=20-2t\) m/s đến khi dừng hẳn. Quãng đường xe đi được từ lúc bắt đầu giảm phanh đến khi dừng hẳn là

	\(98\) m
	\(94\) m
	\(100\) m
	\(96\) m

Một ô tô đang chạy với tốc độ \(36\) km/h thì người lái xe đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v(t)=-5t+10\) m/s, trong đó \(t\) là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

	\(10\) m
	\(20\) m
	\(2\) m
	\(0,2\) m

Tính thể tích khối tròn xoay được tạo bởi hình phẳng giới hạn bởi ba đường \(y=\sqrt{x}\), \(y=2-x\) và \(y=0\) quanh trục \(Ox\).

	\(\dfrac{3\pi}{2}\)
	\(\dfrac{5\pi}{6}\)
	\(\pi\)
	\(\dfrac{2\pi}{3}\)

Cho hình phẳng giới hạn bởi đồ thị hàm số \(y=\mathrm{e}^x\), trục \(Ox\), hai đường thẳng \(x=0\), \(x=1\). Thể tích khối tròn xoay khi quay hình đó xung quanh trục hoành được cho bởi công thức

	\(\left(\pi\displaystyle\int\limits_{0}^{1}\mathrm{e}^x\mathrm{\,d}x\right)^2\)
	\(\pi\displaystyle\int\limits_{0}^{1}\mathrm{e}^{2x}\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{0}^{1}\mathrm{e}^{2x}\mathrm{\,d}x\)
	\(\pi\left(\displaystyle\int\limits_{0}^{1}\mathrm{e}^x\mathrm{\,d}x\right)^2\)

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng \(D\) giới hạn bởi các đường \(y=\sqrt{x-1}\), trục hoành, \(x=2\) và \(x=5\) quanh trục \(Ox\) bằng

	\(\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{2}^{5}\sqrt{x-1}\mathrm{\,d}x\)
	\(\pi\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x\)
	\(\pi^2\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x\)

Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y=x^2\) và \(y=x\) là

	\(1\)
	\(\dfrac{3}{2}\)
	\(\dfrac{1}{2}\)
	\(\dfrac{1}{6}\)

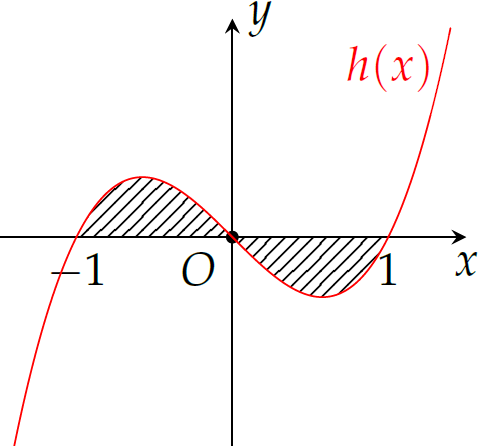
Cho đồ thị hàm số \(y=h(x)\). Diện tích hình phẳng (phần gạch chéo trong hình vẽ) bằng

	\(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{-1}^{1}h(x)\mathrm{\,d}x\)
	\(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{0}h(x)\mathrm{\,d}x\)
	\(-\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\)

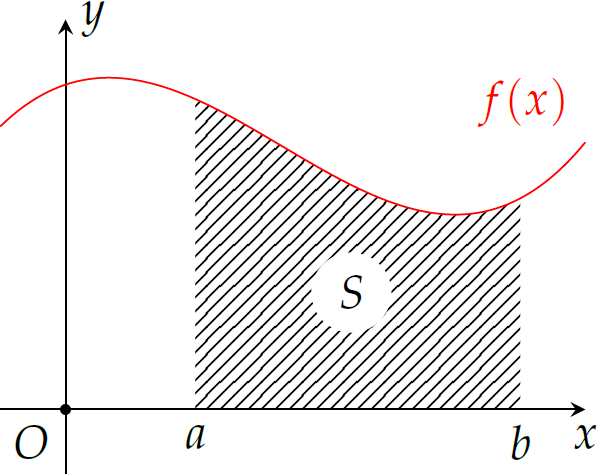
Diện tích hình phẳng \(S\) đối với hình vẽ trên là

	\(S=-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\)
	\(S=\displaystyle\int\limits_{a}^{b}-f(x)\mathrm{\,d}x\)

Biết rằng \(\displaystyle\int\limits_{1}^{5}\dfrac{3}{x^2+3x}\mathrm{\,d}x=a\ln5+b\ln2\), (\(a,\,b\in\mathbb{Z}\)). Mệnh đề nào sau đây đúng?

	\(a+b=0\)
	\(a-b=0\)
	\(a+2b=0\)
	\(2a-b=0\)

Cho \(\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{2}}\dfrac{\cos x}{\sin x+1}\mathrm{\,d}x=a\ln2+b\ln3\) (\(a,\,b\in\mathbb{Z}\)). Khi đó, giá trị của \(a\cdot b\) là

	\(2\)
	\(-2\)
	\(-4\)
	\(3\)

Kết quả của phép tính tích phân \(\displaystyle\int\limits_{0}^{1}\ln(2x+1)\mathrm{\,d}x=a\ln3+b\), (\(a,\,b\in\mathbb{Q}\)) khi đó giá trị của \(ab^3\) bằng

	\(-\dfrac{3}{2}\)
	\(3\)
	\(1\)
	\(\dfrac{3}{2}\)

Cho \(I=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin2x\mathrm{\,d}x\), \(J=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin x\mathrm{\,d}x\). Trong các mệnh đề sau, mệnh đề nào đúng?

	\(I>J\)
	\(I=J\)
	\(I< J\)
	\(I=2J\)