Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ và có đồ thị $f'(x)$ như hình vẽ.

Tìm số điểm cực trị của hàm số $g(x)=f(x)-x$.
| $1$ | |
| $2$ | |
| $3$ | |
| $4$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ và có đồ thị $f'(x)$ như hình vẽ.
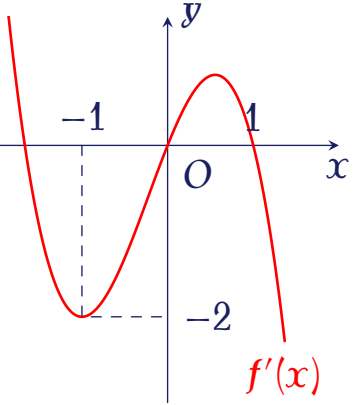
Số điểm cực trị của hàm số $y=f(x)+2x$ là
| $1$ | |
| $2$ | |
| $3$ | |
| $4$ |
Tìm các giá trị thực của tham số $m$ để đồ thị hàm số $y=x^4-2mx^2$ có ba điểm cực trị tạo thành một tam giác có diện tích bằng $4\sqrt{2}$.
| $m=2$ | |
| $m=-2$ | |
| $m=\pm2$ | |
| $m=32$ |
Cho hàm số $y=\dfrac{x^4}{4}-(3m+1)x^2+2(m+1)$ với $m$ là tham số thực. Tìm giá trị của $m$ để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có trọng tâm là gốc tọa độ.
| $m=-\dfrac{2}{3}$ | |
| $m=\dfrac{2}{3}$ | |
| $m=-\dfrac{1}{3}$ | |
| $m=\dfrac{1}{3}$ |
Cho hàm số $y=\dfrac{9}{8}x^4+3(m-3)x^2+4m+2022$ với $m$ là tham số thực. Tìm giá trị của $m$ để đồ thị hàm số có ba điểm cực trị tạo thành tam giác đều.
| $m=-2$ | |
| $m=2$ | |
| $m=3$ | |
| $m=2022$ |
Cho hàm số $y=x^4-2(m+1)x^2+m^2$ với $m$ là tham số thực. Tìm tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành một tam giác vuông.
| $m=-1$ | |
| $m=0$ | |
| $m=1$ | |
| $m>-1$ |
Gọi $x_1,\,x_2$ là hai điểm cực trị của hàm số $y=4x^3+mx^2-3x$. Tìm các giá trị của tham số $m$ sao cho $x_1+4x_2=0$.
| $m=0$ | |
| $m=\pm\dfrac{9}{2}$ | |
| $m=\pm\dfrac{3}{2}$ | |
| $m=\pm\dfrac{1}{2}$ |
Gọi $x_1,\,x_2$ là hai điểm cực trị của hàm số $y=x^3-3mx^2+3\big(m^2-1\big)x-m^3+m$. Tìm các giá trị của tham số $m$ sao cho $x_1^2+x_2^2-x_1x_2=7$.
| $m=0$ | |
| $m=\pm\dfrac{9}{2}$ | |
| $m=\pm\dfrac{1}{2}$ | |
| $m=\pm2$ |
Gọi $S$ là tập hợp các giá trị nguyên để hàm số $y=\dfrac{x^3}{3}-(m+1)x^2+(m-2)x+2m-3$ đạt cực trị tại hai điểm $x_1,\,x_2$ thỏa mãn $x_1^2+x_2^2=18$. Tính tổng $P$ của tất cả các giá trị $m$ trong $S$.
| $P=-4$ | |
| $P=1$ | |
| $P=-\dfrac{3}{2}$ | |
| $P=-5$ |
Tìm giá trị của tham số $m$ để hàm số $y=x^3-3x^2+mx-1$ có hai điểm cực trị $x_1,\,x_2$ thỏa mãn $x_1^2+x_2^2=6$.
| $m=1$ | |
| $m=-1$ | |
| $m=3$ | |
| $m=-3$ |
Viết phương trình đường thẳng đi qua hai điểm cực tiểu của đồ thị hàm số $y=\dfrac{x^4}{4}+\dfrac{x^3}{3}-x^2$.
| $y=\dfrac{3}{4}x-\dfrac{7}{6}$ | |
| $y=\dfrac{4}{3}x$ | |
| $y=-\dfrac{21}{50}x$ | |
| $y=-\dfrac{3}{4}x-\dfrac{7}{6}$ |
Đồ thị hàm số $y=x^3-3x^2-9x+1$ có hai điểm cực trị là $A$ và $B$. Điểm nào sau đây thuộc đường thẳng $AB$?
| $M(0;-1)$ | |
| $Q(-1;10)$ | |
| $P(1;0)$ | |
| $N(1;-10)$ |
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=-2x^3+3x^2+1$.
| $y=x+1$ | |
| $y=-x+1$ | |
| $y=x-1$ | |
| $y=-x-1$ |
Biết đồ thị hàm số $y=x^3-3x+1$ có hai điểm cực trị $A,\,B$. Khi đó đường thẳng $AB$ có phương trình
| $y=2x-1$ | |
| $y=x-2$ | |
| $y=-x+2$ | |
| $y=-2x+1$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ.
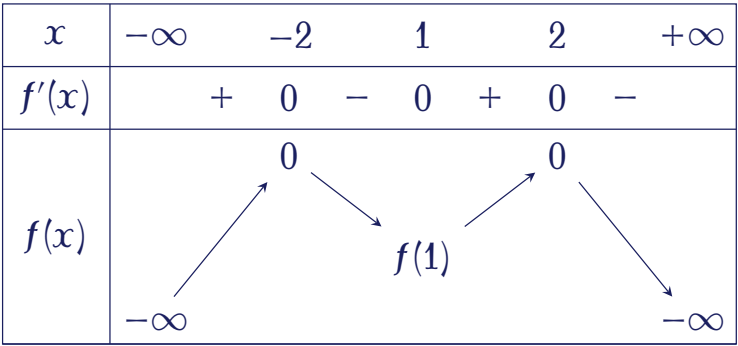
Hàm số $g(x)=\big[f(3-x)\big]^2$ nghịch biến trên khoảng nào trong các khoảng sau?
| $(-2;5)$ | |
| $(1;2)$ | |
| $(2;5)$ | |
| $(5;+\infty)$ |
Cho hàm số $y=f(x)$ có đạo hàm, liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ.
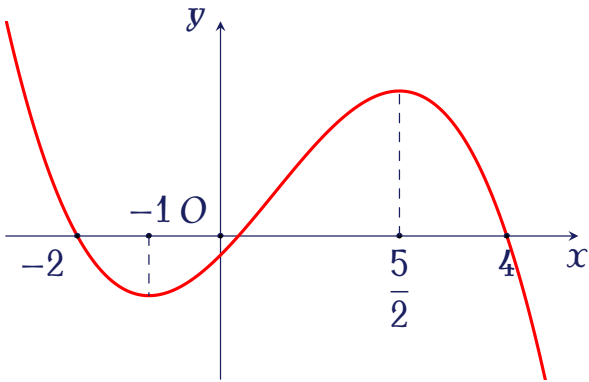
Hàm số $g(x)=\big[f(x)\big]^2$ nghịch biến trên khoảng nào sau đây?
| $(-1;1)$ | |
| $\left(0;\dfrac{5}{2}\right)$ | |
| $\left(\dfrac{5}{2};4\right)$ | |
| $(-2;-1)$ |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$. Biết hàm số $f'(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ.
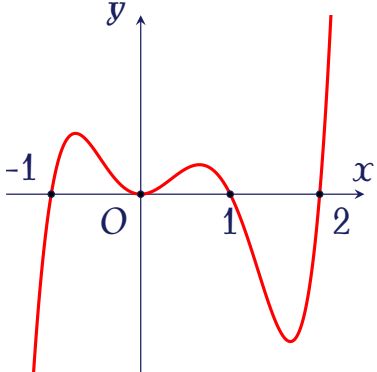
Hàm số $g(x)=f\left(\sqrt{x^2+1}\right)$ đồng biến trên khoảng
| $\left(-\infty;-\sqrt{3}\right)$ và $\left(0;\sqrt{3}\right)$ | |
| $\left(-\infty;-\sqrt{3}\right)$ và $\left(\sqrt{3};+\infty\right)$ | |
| $\left(-\sqrt{3};0\right)$ và $\left(\sqrt{3};+\infty\right)$ | |
| $\left(-\infty;-\sqrt{3}\right)$ và $\left(0;+\infty\right)$ |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có đồ thị hàm $f'(x)$ như hình vẽ.
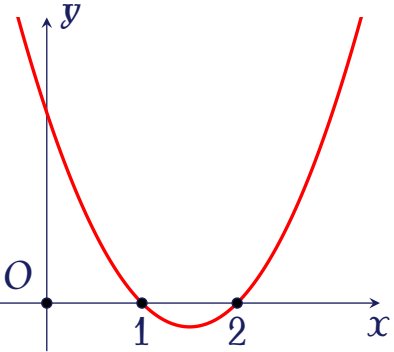
Tìm khoảng nghịch biến của hàm số $g(x)=f\big(x-x^2\big)$.
| $\left(-\dfrac{1}{2};+\infty\right)$ | |
| $\left(-\dfrac{3}{2};+\infty\right)$ | |
| $\left(-\infty;\dfrac{3}{2}\right)$ | |
| $\left(\dfrac{1}{2};+\infty\right)$ |
Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số $y=\dfrac{mx^3}{3}+7mx^2+14x-m+2$ nghịch biến trên $[1;+\infty)$.
| $\left(-\infty;-\dfrac{14}{15}\right)$ | |
| $\left(-\infty;-\dfrac{14}{15}\right]$ | |
| $\left[-2;-\dfrac{14}{15}\right]$ | |
| $\left[-\dfrac{14}{15};+\infty\right)$ |
Tìm tập hợp giá trị của tham số $m$ để hàm số $y=x^3-mx^2-(m-6)x+1$ đồng biến trên khoảng $(0;4)$.
| $(-\infty;6]$ | |
| $(-\infty;3]$ | |
| $(-\infty;3)$ | |
| $[3;6]$ |
