Cho hàm số \(y=\dfrac{3x-1}{x+2}\). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn \([0;2]\). Khi đó \(4M-2m\) bằng
| \(10\) | |
| \(6\) | |
| \(5\) | |
| \(4\) |
Kí hiệu $M$ và $m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số $y=x^2+\sqrt{4-x^2}$. Khi đó $M+m$ bằng
| $\dfrac{25}{4}$ | |
| $\dfrac{15}{4}$ | |
| $4$ | |
| $\dfrac{1}{4}$ |
Có bao nhiêu giá trị nguyên thuộc đoạn $[-10;10]$ của $m$ để giá trị lớn nhất của hàm số $y=\dfrac{2x+m}{x+1}$ trên đoạn $[-4;-2]$ không lớn hơn $1$?
| $6$ | |
| $7$ | |
| $8$ | |
| $5$ |
Đồ thị của hàm số $y=f(x)$ có dạng như đường cong trong hình vẽ bên.
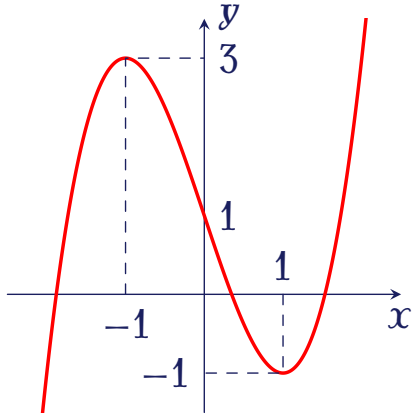
Gọi $M$ là giá trị lớn nhất, $m$ là giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $[-1;1]$. Tính $P=M-2m$.
| $P=5$ | |
| $P=3$ | |
| $P=1$ | |
| $P=4$ |
Cho hàm số $f(x)=\dfrac{x+m}{x+1}$ với $m$ là tham số thực. Tìm giá trị của $m$ thỏa mãn $\min\limits_{[1;2]}f(x)+\min\limits_{[1;2]}f(x)=\dfrac{16}{3}$.
| $m=5$ | |
| $m=\dfrac{5}{6}$ | |
| $m=-5$ | |
| $m=\dfrac{5}{3}$ |
Cho hàm số $f(x)=\dfrac{x+m}{x-1}$ với $m$ là tham số thực. Gọi $m$ là giá trị thỏa mãn $\min\limits_{[2;4]}=3$, mệnh đề nào sau đây là đúng?
| $3< m\leq4$ | |
| $1\leq m<3$ | |
| $m>4$ | |
| $m<-1$ |
Cho hàm số $f(x)=\dfrac{x-m^2}{x+8}$ với $m$ là tham số thực. Tìm giá trị lớn nhất của $m$ để hàm số có giá trị nhỏ nhất trên đoạn $[0;3]$ bằng $-2$.
| $m=-4$ | |
| $m=5$ | |
| $m=1$ | |
| $m=4$ |
Cho hàm số $f\left(x\right)=\log_2^3x-\log_2x^3+m$ ($m$ là tham số thực). Gọi $S$ là tập hợp tất cả các giá trị của $m$ sao cho $\max\limits_{\left[1;4\right]}\left|f\left(x\right)\right|+\min\limits_{\left[1;4\right]}\left|f\left(x\right)\right|=6$. Tổng bình phương các phần tử của $S$ bằng
| $13$ | |
| $18$ | |
| $5$ | |
| $8$ |
Giá trị lớn nhất của hàm số $f\left(x\right)=\dfrac{2x+5}{x-2}$ trên đoạn $\left[3;6\right]$ là
| $f\left(5\right)$ | |
| $f\left(4\right)$ | |
| $f\left(6\right)$ | |
| $ f\left(3\right)$ |
Gọi $M,\,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $f(x)=x^4-2x^2+3$ trên đoạn $[0;2]$. Tổng $M+m$ bằng
| $11$ | |
| $14$ | |
| $5$ | |
| $13$ |
Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x+\dfrac{1}{x}\) trên đoạn \(\left[\dfrac{1}{2};3\right]\). Khi đó \(M+m\) bằng
| \(\dfrac{9}{2}\) | |
| \(\dfrac{35}{6}\) | |
| \(\dfrac{7}{2}\) | |
| \(\dfrac{16}{3}\) |
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-3;2]\) và có bảng biến thiên như sau: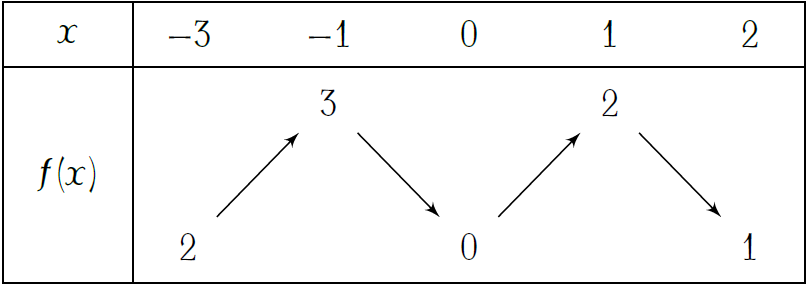
Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(f(x)\) trên đoạn \([-1;2]\). Tính \(M+m\).
| \(3\) | |
| \(2\) | |
| \(1\) | |
| \(4\) |
Gọi \(M,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y=x^3-3x^2+1\) trên đoạn \([1;2]\). Khi đó tổng \(M+N\) bằng
| \(2\) | |
| \(-2\) | |
| \(0\) | |
| \(-4\) |
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x\sqrt{1-x^2}\). Khi đó \(M-m\) bằng
| \(1\) | |
| \(2\) | |
| \(4\) | |
| \(3\) |
Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+3}{2x-3}\) trên đoạn \([2;5]\).
| \(\dfrac{7}{8}\) | |
| \(\dfrac{8}{7}\) | |
| \(5\) | |
| \(\dfrac{2}{7}\) |
Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+1}{x-1}\) trên đoạn \([2;3]\).
| \(-3\) | |
| \(3\) | |
| \(2\) | |
| \(4\) |
Tìm giá trị lớn nhất của hàm số \(y=\dfrac{3x-1}{x-3}\) trên đoạn \([0;2]\).
| \(-\dfrac{1}{3}\) | |
| \(-5\) | |
| \(5\) | |
| \(\dfrac{1}{3}\) |
Hàm số nào sau đây không có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \([-2;2]\).
| \(y=\dfrac{x-1}{x+1}\) | |
| \(y=x^2\) | |
| \(y=1-x\) | |
| \(y=x^3+2\) |
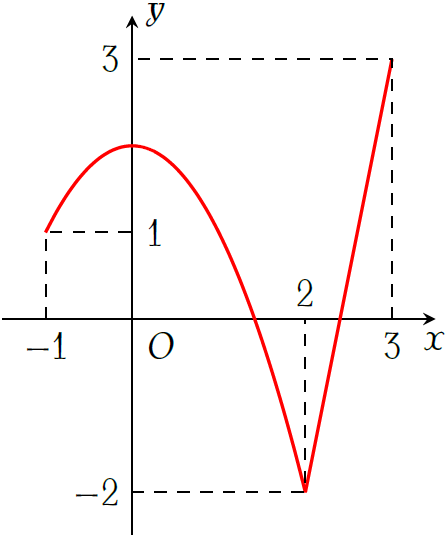
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \([-1;3]\). Giá trị của \(M-m\) bằng
| \(0\) | |
| \(1\) | |
| \(4\) | |
| \(5\) |
Cho hàm số \(f\left(x\right)=\dfrac{x+m}{x+1}\) (\(m\) là tham số thực). Gọi \(S\) là tập hợp tất cả các giá trị của m sao cho $$\max\limits_{[0;1]}\left|f\left(x\right)\right|+\min\limits_{[0;1]}\left|f\left(x\right)\right|=2.$$Số phần tử của \(S\) là
| \(6\) | |
| \(2\) | |
| \(1\) | |
| \(4\) |
