Giải bất phương trình $\dfrac{x+11}{5-6x}$.

Giải bất phương trình $\dfrac{1}{x-1}+\dfrac{2}{x-2}>0$.

Giải bất phương trình $\dfrac{x^2-x-6}{2-x}\geq0$.

Hàm số $y=\left(3-x\right)\left(x+2\right)^2\left(x-2\right)^3$ nhận giá trị dương trên khoảng nào dưới đây?

	$\left(-2;2\right)$
	$\left(3;+\infty\right)$
	$\left(2;3\right)$
	$\left(-\infty;-2\right)$

Cho biểu thức $f\left(x\right)=\dfrac{1}{3x-6}$. Tìm tập hợp các giá trị $x$ để $f\left(x\right)>0$.

	$\left(-\infty;2\right]$
	$\left(-\infty;2\right)$
	$\left(2;+\infty\right)$
	$\left[2;+\infty\right)$

Cho biểu thức $f\left(x\right)=\left(x+5\right)\left(3-x\right)$. Tìm tập hợp các giá trị $x$ để $f\left(x\right)\leq0$.

	$\left(-\infty;-5\right)\cup\left(3;+\infty\right)$
	$\left(3;+\infty\right)$
	$\left(-5;-3\right)$
	$\left(-\infty;-5\right]\cup\left[3;+\infty\right)$

Tập nghiệm của bất phương trình \(\dfrac{3x-1}{x^2-4}\geq0\) là tập hợp nào sau đây?

	\(T=\left(-2;\dfrac{1}{3}\right]\cup(2;+\infty)\)
	\(P=(-\infty;-2)\cup(2;+\infty)\)
	\(Q=(-2;2)\)
	\(S=(-\infty;-2)\cup\left[\dfrac{1}{3};2\right)\)

Tìm tập nghiệm \(S\) của bất phương trình \(\dfrac{1}{x-1}\leq1\).

	\(S=(-\infty;2]\)
	\(S=(1;+\infty)\)
	\(S=(1;2]\)
	\(S=(-\infty;1)\cup[2;+\infty)\)

Tìm tất cả các nghiệm của bất phương trình \((2x-3)(5-3x)>0\).

	\(x<\dfrac{3}{2},\,x>\dfrac{5}{3}\)
	\(x>\dfrac{5}{3}\)
	\(\dfrac{3}{2}< x<\dfrac{5}{3}\)
	\(x<\dfrac{3}{2}\)

Cho nhị thức bậc nhất \(f(x)=ax+b\,(a\neq0)\) có bảng xét dấu như hình vẽ bên dưới. Mệnh đề nào sau đây sai?

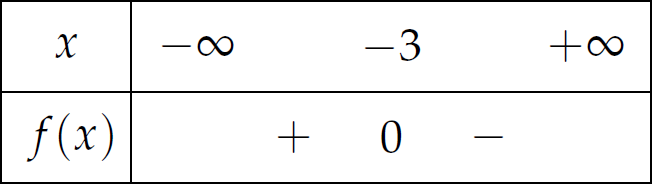
	Phương trình \(f(x)=0\) có nghiệm \(x=-3\)
	\(f(-4)< f(-1)\)
	\(f(x)>0\) với mọi \(x\in(-\infty;-3)\)
	\(a\) là một số thực âm

Tập nghiệm của bất phương trình \(\dfrac{-3x^2+2x+5}{x-1}\leq0\) là

	\((-\infty;-1]\cup\left[\dfrac{5}{3};+\infty\right)\)
	\((-1;1)\cup\left(\dfrac{5}{3};+\infty\right)\)
	\([-1;1]\cup\left[\dfrac{5}{3};+\infty\right)\)
	\([-1;1)\cup\left[\dfrac{5}{3};+\infty\right)\)

Bất phương trình \(\dfrac{1}{x-1}+\dfrac{2}{x-2}>0\) có tập nghiệm là

	\(\left(1;\dfrac{4}{3}\right]\cup(2;+\infty)\)
	\(\left(1;\dfrac{4}{3}\right)\cup(2;+\infty)\)
	\((-\infty;1)\cup\left[\dfrac{4}{3};2\right)\)
	\(\left(\dfrac{4}{3};2\right)\cup(-\infty;1)\)

Tập nghiệm của bất phương trình \(\dfrac{x-1}{x+2}<0\) là

	\((-2;1)\)
	\((-2;1]\)
	\((-\infty;-2)\cup(1;+\infty)\)
	\((-\infty;-2)\cup[1;+\infty)\)

Biểu thức \(f(x)=2x-3\) nhận giá trị dương trên khoảng

	\((2;+\infty)\)
	\(\left(\dfrac{2}{3};+\infty\right)\)
	\(\left(-\infty;\dfrac{3}{2}\right)\)
	\(\left(\dfrac{3}{2};+\infty\right)\)

Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn $$\dfrac{x+3}{x^2-4}-\dfrac{1}{x+2}<\dfrac{2x}{2x-x^2}?$$

	\(0\)
	\(2\)
	\(1\)
	\(3\)

Tập nghiệm \(S\) của bất phương trình \(\dfrac{x-7}{4x^2-19x+12}>0\) là

	\(S=\left(-\infty;\dfrac{3}{4}\right)\cup(4;7)\)
	\(S=\left(\dfrac{3}{4};4\right)\cup(7;+\infty)\)
	\(S=\left(\dfrac{3}{4};4\right)\cup(4;+\infty)\)
	\(S=\left(\dfrac{3}{4};7\right)\cup(7;+\infty)\)

Giải bất phương trình \(x^3+3x^2-6x-8\geq0\).

	\(S=[-4;-1]\cup[2;+\infty)\)
	\(S=(-4;-1)\cup(2;+\infty)\)
	\(S=[-1;+\infty)\)
	\(S=(-\infty;-4]\cup[-1;2]\)

Biểu thức \(f(x)=\dfrac{11x+3}{-x^2+5x-7}\) nhận giá trị dương khi và chỉ khi

	\(x\in\left(-\dfrac{3}{11};+\infty\right)\)
	\(x\in\left(-\dfrac{3}{11};5\right)\cup\left(\dfrac{5}{4};3\right)\)
	\(x\in\left(-\infty;-\dfrac{3}{11}\right)\)
	\(x\in\left(-5;-\dfrac{3}{11}\right)\)

Biểu thức \(\left(3x^2-10x+3\right)(4x-5)\) âm khi và chỉ khi

	\(x\in\left(-\infty;\dfrac{5}{4}\right)\)
	\(x\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{5}{4};3\right)\)
	\(x\in\left(\dfrac{1}{3};\dfrac{5}{4}\right)\cup(3;+\infty)\)
	\(x\in\left(\dfrac{1}{3};3\right)\)

Để phương trình \((m-1)x^2+3mx+m^2-m-6=0\) có hai nghiệm trái dấu thì

	\(m\in(-\infty;-2)\cup(1;3)\)
	\(m\in(-\infty;-2]\cup[1;3]\)
	\(m\in(-2;1)\cup(3;+\infty)\)
	\(m\in[-2;1]\cup[3;+\infty)\)