Một hộp chứa $15$ quả cầu gồm $6$ quả màu đỏ được đánh số từ $1$ đến $6$ và $9$ quả màu xanh được đánh số từ $1$ đến $9$. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
| $\dfrac{9}{35}$ | |
| $\dfrac{18}{35}$ | |
| $\dfrac{4}{35}$ | |
| $\dfrac{1}{7}$ |
Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-2)^2(1-x)$ với mọi $x\in\mathbb{R}$. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
| $(1;2)$ | |
| $(1;+\infty)$ | |
| $(2;+\infty)$ | |
| $(-\infty;1)$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
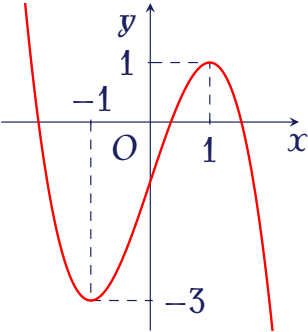
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(x)=m$ có ba nghiệm thực phân biệt?
| $2$ | |
| $5$ | |
| $3$ | |
| $4$ |
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, $SA$ vuông góc với đáy và $SA=AB$ (tham khảo hình bên).
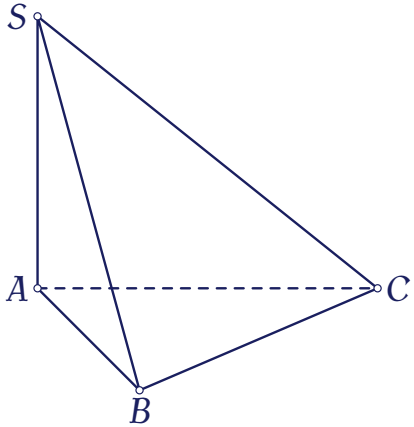
Góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ bằng
| $60^{\circ}$ | |
| $30^{\circ}$ | |
| $90^{\circ}$ | |
| $45^{\circ}$ |
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường $y=-x^2+2x$ và $y=0$ quanh trục $Ox$ bằng
| $\dfrac{16}{15}$ | |
| $\dfrac{16\pi}{9}$ | |
| $\dfrac{16}{9}$ | |
| $\dfrac{16\pi}{15}$ |
Với $a$ là số thực dương tùy ý, $\ln(3a)-\ln(2a)$ bằng
| $\ln a$ | |
| $\ln\dfrac{2}{3}$ | |
| $\ln\big(6a^2\big)$ | |
| $\ln\dfrac{3}{2}$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
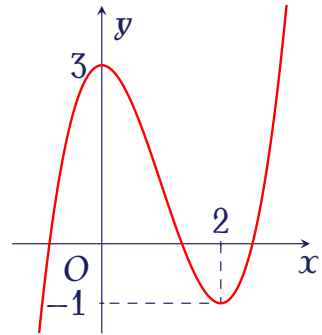
Giá trị cực đại của hàm số đã cho là
| $-1$ | |
| $3$ | |
| $2$ | |
| $0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
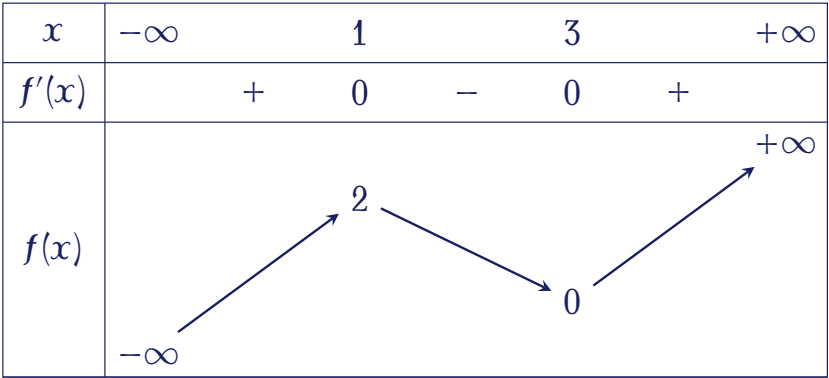
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(0;2)$ | |
| $(3;+\infty)$ | |
| $(-\infty;1)$ | |
| $(1;3)$ |
Cho hàm số $f(x)=\cos x+x$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\sin x+x^2+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\sin x+x^2+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\sin x+\dfrac{x^2}{2}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\sin x+\dfrac{x^2}{2}+C$ |
Nếu $\displaystyle\displaystyle\int_0^2f(x)\mathrm{\,d}x=4$ thì $\displaystyle\displaystyle\int_0^2\left[\dfrac{1}{2}f(x)-2\right]\mathrm{\,d}x$ bằng
| $0$ | |
| $6$ | |
| $8$ | |
| $-2$ |
Cho $\displaystyle\displaystyle\int\dfrac{1}{x}\mathrm{\,d}x=F(x)+C$. Khẳng định nào dưới đây đúng?
| $F'(x)=\dfrac{2}{x^2}$ | |
| $F'(x)=\ln x$ | |
| $F'(x)=\dfrac{1}{x}$ | |
| $F'(x)=-\dfrac{1}{x^2}$ |
Cho tập hợp $A$ có $15$ phần tử. Số tập con gồm hai phần tử của $A$ bằng
| $225$ | |
| $30$ | |
| $210$ | |
| $105$ |
Tập nghiệm của bất phương trình $\log(x-2)>0$ là
| $(2;3)$ | |
| $(-\infty;3)$ | |
| $(3;+\infty)$ | |
| $(12;+\infty)$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x+1}{3x-1}$ là đường thẳng có phương trình
| $y=\dfrac{1}{3}$ | |
| $y=-\dfrac{2}{3}$ | |
| $y=-\dfrac{1}{3}$ | |
| $y=\dfrac{2}{3}$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
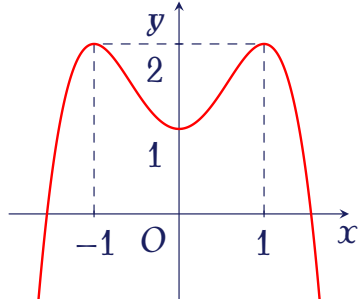
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
| $(-1;2)$ | |
| $(0;1)$ | |
| $(1;2)$ | |
| $(1;0)$ |
Trong không gian $Oxyz$, cho đường thẳng $d\colon\dfrac{x-1}{2}=\dfrac{y-2}{-1}=\dfrac{z+3}{-2}$. Điểm nào dưới đây thuộc $d$?
| $P(1;2;3)$ | |
| $Q(1;2;-3)$ | |
| $N(2;1;2)$ | |
| $M(2;-1;-2)$ |
Cho hình nón có đường kính đáy $2r$ và độ dải đường sinh $\ell$. Diện tích xung quanh của hình nón đã cho bằng
| $2\pi r\ell$ | |
| $\dfrac{2}{3}\pi r\ell^2$ | |
| $\pi r\ell$ | |
| $\dfrac{1}{3}\pi r^2\ell$ |
Cho mặt phẳng $(P)$ tiếp xúc với mặt cầu $S(O,R)$. Gọi $d$ là khoảng cách từ $O$ đến $(P)$. Khẳng định nào dưới đây đúng?
| $d< R$ | |
| $d>R$ | |
| $d=R$ | |
| $d=0$ |
Cho khối chóp $S.ABC$ có đáy là tam giác vuông cân tại $A$, $AB=2$, $SA$ vuông góc với đáy và $SA=3$ (tham khảo hình bên).
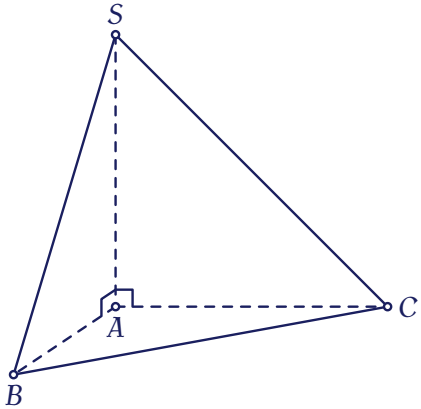
Thể tích khối chóp đã cho bằng
| $12$ | |
| $2$ | |
| $6$ | |
| $4$ |
