Cho \(x\) là một phần tử của tập hợp \(A\). Xét các mệnh đề sau:

1. \(x\in A\)
2. \(\{x\}\in A\)
3. \(x\subset A\)
4. \(\{x\}\subset A\)

Trong các mệnh đề trên, mệnh đề nào đúng?

	I và II
	I và III
	I và IV
	II và IV

Cho \(A\) là một tập hợp. Trong các mệnh đề sau, mệnh đề nào đúng?

	\(A\in A\)
	\(\varnothing\in A\)
	\(A\subset A\)
	\(A\in\{A\}\)

Hình nào sau đây minh họa tập \(A\) là tập con của tập \(B\)?

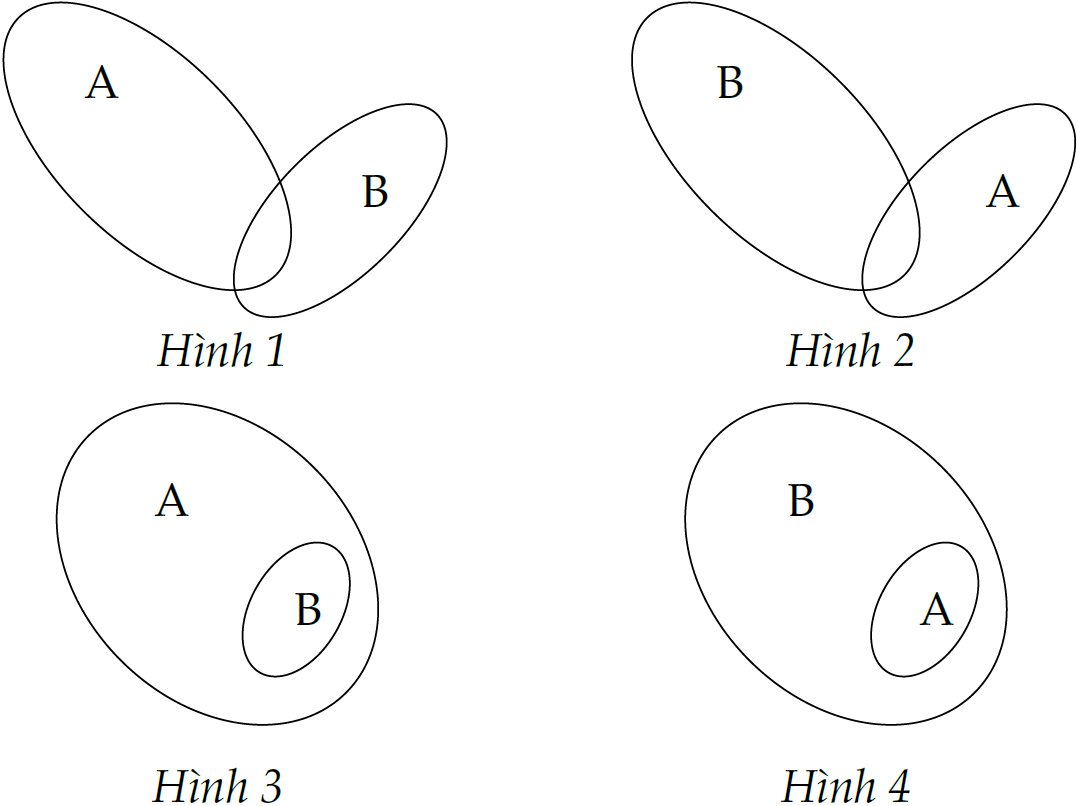
	Hình 1
	Hình 2
	Hình 3
	Hình 4

Cho tập hợp \(M=\left\{(x;y)\colon x,\,y\in\mathbb{N}\text{ và }x+y=1\right\}\). Hỏi \(M\) có bao nhiêu phần tử?

	\(0\)
	\(1\)
	\(2\)
	\(4\)

Tập hợp nào sau đây là tập rỗng?

	\(A=\{\varnothing\}\)
	\(B=\left\{x\in\mathbb{N}\colon(3x-2)\left(3x^2+4x+1\right)=0\right\}\)
	\(C=\left\{x\in\mathbb{Z}\colon(3x-2)\left(3x^2+4x+1\right)=0\right\}\)
	\(D=\left\{x\in\mathbb{Q}\colon(3x-2)\left(3x^2+4x+1\right)=0\right\}\)

Tập hợp \(A=\left\{k^2+1\colon k\in\mathbb{Z},\,|k|\leq2\right\}\) có bao nhiêu phần tử?

	\(1\)
	\(2\)
	\(3\)
	\(5\)

Cho tập hợp $$A=\left\{x\in\mathbb{N}\colon x\text{ là ước chung của }36\text{ và }120\right\}$$Hãy liệt kê các phần tử của tập hợp \(A\).

	\(A=\{1;2;3;4;6;12\}\)
	\(A=\{1;2;4;6;8;12\}\)
	\(A=\{2;4;6;8;10;12\}\)
	\(A=\{1;36;120\}\)

Hãy liệt kê các phần tử của tập hợp $$X=\left\{x\in\mathbb{R}\colon x^2+x+1=0\right\}$$

	\(X=0\)
	\(X=\{0\}\)
	\(X=\varnothing\)
	\(X=\{\varnothing\}\)

Hãy liệt kê các phần tử của tập hợp $$X=\left\{x\in\mathbb{Q}\colon\left(x^2-x-6\right)\left(x^2-5\right)=0\right\}$$

	\(X=\left\{\sqrt{5};3\right\}\)
	\(X=\left\{-\sqrt{5};-2;\sqrt{5};3\right\}\)
	\(X=\left\{-2;3\right\}\)
	\(X=\left\{-\sqrt{5};\sqrt{5}\right\}\)

Cho tập hợp \(X=\left\{x\in\mathbb{Z}\colon\left(x^2-9\right)\left(x^2-\left(1+\sqrt{2}\right)x+\sqrt{2}\right)=0\right\}\). Hỏi tập \(X\) có bao nhiêu phần tử?

	\(1\)
	\(2\)
	\(3\)
	\(4\)

Cho tập hợp \(X=\left\{x\in\mathbb{N}\colon\left(x^2-4\right)(x-1)\left(2x^2-7x+3\right)=0\right\}\). Tính tổng \(S\) các phần tử của tập hợp \(X\).

	\(S=4\)
	\(S=\dfrac{9}{2}\)
	\(S=5\)
	\(S=6\)

Hãy viết tập hợp \(X=\left\{x\in\mathbb{R}\colon2x^2-5x+3=0\right\}\) dưới dạng liệt kê phần tử.

	\(X=\{0\}\)
	\(X=\{1\}\)
	\(X=\left\{\dfrac{3}{2}\right\}\)
	\(X=\left\{1;\dfrac{3}{2}\right\}\)

Mệnh đề nào sau đây tương đương với mệnh đề \(A\neq\varnothing\)?

	\(\forall x,\,x\in A\)
	\(\exists x,\,x\in A\)
	\(\exists x,\,x\notin A\)
	\(\forall x,\,x\subset A\)

Kí hiệu nào sau đây dùng để viết đúng mệnh đề "\(\sqrt{2}\) không phải là số vô tỉ"?

	\(\sqrt{2}\neq\mathbb{Q}\)
	\(\sqrt{2}\not\subset\mathbb{Q}\)
	\(\sqrt{2}\notin\mathbb{Q}\)
	\(\sqrt{2}\in\mathbb{Q}\)

Kí hiệu nào sau đây dùng để viết đúng mệnh đề "\(7\) là số tự nhiên"?

	\(7\subset\mathbb{N}\)
	\(7\in\mathbb{N}\)
	\(7\notin\mathbb{N}\)
	\(7\leq\mathbb{N}\)

Trong các mệnh đề sau đây, mệnh đề nào sai?

	\(\forall x\in\mathbb{R},\,\exists y\in\mathbb{R}\colon x+y^2\geq0\)
	\(\exists x\in\mathbb{R},\,\forall y\in\mathbb{R}\colon x+y^2\geq0\)
	\(\forall x\in\mathbb{R},\,\forall y\in\mathbb{R}\colon x+y^2\geq0\)
	\(\exists x\in\mathbb{R},\,\forall y\in\mathbb{R}\colon x+y^2\leq0\)

Trong các mệnh đề sau đây, mệnh đề nào sai?

	\(\exists x\in\mathbb{Z},\,2x^2-8=0\)
	\(\exists n\in\mathbb{N},\,n^2+11n+2\) chia hết cho \(11\)
	Tồn tại số nguyên tố chia hết cho \(5\)
	\(\exists n\in\mathbb{N},\,n^2+1\) chia hết cho \(4\)

Trong các mệnh đề sau đây, mệnh đề nào đúng?

	Không có số chẵn nào là số nguyên tố
	\(\forall x\in\mathbb{R},\,-x^2<0\)
	\(\exists n\in\mathbb{N},\,n(n+11)+6\) chia hết cho \(11\)
	Phương trình \(3x^2-6=0\) có nghiệm hửu tỷ

Mệnh đề "\(\exists x\in\mathbb{R},\,x^2=2\)" khẳng định rằng

	Bình phương của mọi số thưc đều bằng \(2\)
	Có ít nhất một số thực có bình phương bằng \(2\)
	Chỉ có một số thực có bình phương bằng \(2\)
	Nếu \(x\) là một số thực thì \(x^2=2\)

Kí hiệu \(X\) là tập hợp các cầu thủ \(x\) trong đổi tuyển bóng rổ, \(P(x)\) là mệnh đề chứa biến "\(x\) cao trên \(180\)cm". Mệnh đề "\(\forall x\in X,\,P(x)\)" khẳng định rằng

	Mọi cầu thủ trong đổi tuyển bóng rổ đều cao trên \(180\)cm
	Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao trên \(180\)cm
	Bất cứ ai cao trên \(180\)cm đều là cầu thủ của đội tuyển bóng rổ
	Có một số người cao trên \(180\)cm là cầu thủ của đội tuyển bóng rổ