Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$
| Không tồn tại | |
| Đi qua điểm $S$ | |
| Đi qua giao điểm $I$ của $AD$ và $BC$ | |
| Đi qua giao điểm $I$ của $AB$ và $CD$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
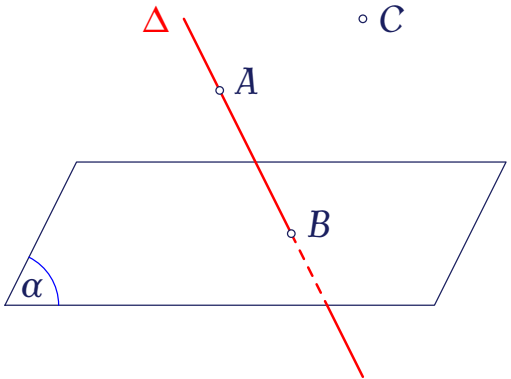
Giao tuyến của hai mặt phẳng $(\alpha)$ và $(ABC)$ có tồn tại không, nếu có thì giao tuyến đó đi qua điểm nào?
| $B$ | |
| $A$ | |
| $C$ | |
| Không tồn tại |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
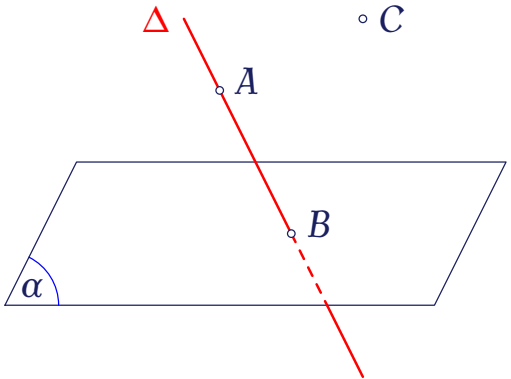
Mệnh đề nào sau đây là đúng?
| $\Delta\subset(\alpha)$ | |
| $\Delta\cap(\alpha)=A$ | |
| $C\in(\alpha)$ | |
| $\Delta\cap(\alpha)=B$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
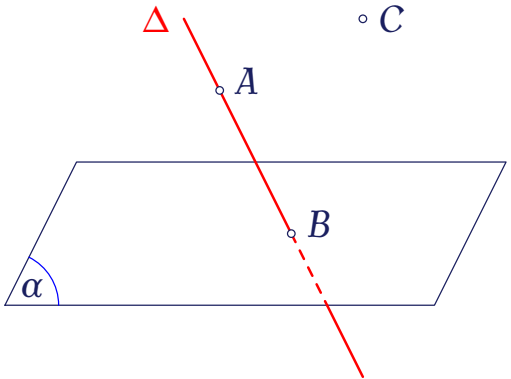
Xét mệnh đề "$B=\Delta\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
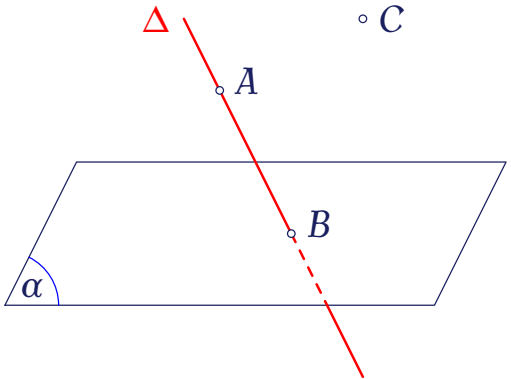
Xét mệnh đề "$C\ldots\ldots\Delta$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
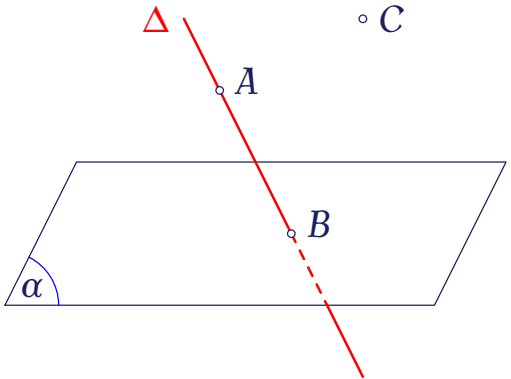
Xét mệnh đề "$A\ldots\ldots\Delta$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
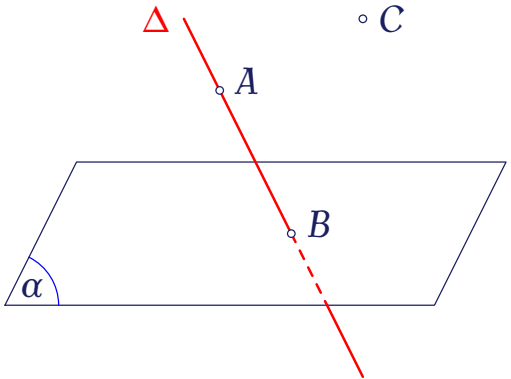
Xét mệnh đề "$A\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
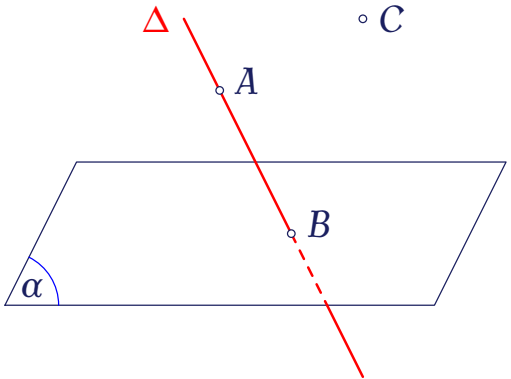
Xét mệnh đề "$B\ldots\ldots(\alpha)$", hãy chọn ký hiệu thích hợp điền vào dấu "..." để được mệnh đề đúng.
| $\notin$ | |
| $\in$ | |
| $\subset$ | |
| $\cap$ |
Trong không gian, cho mặt phẳng $(\alpha)$, đường thẳng $\Delta$ và các điểm $A,\,B,\,C$ như hình vẽ.
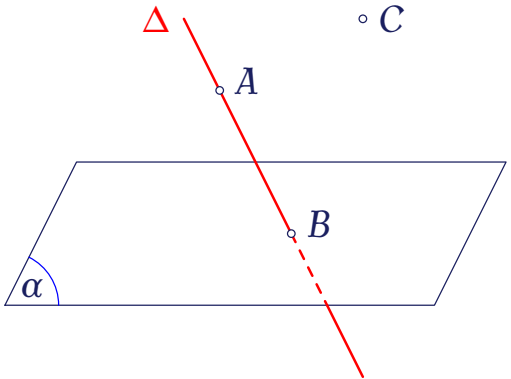
Phần nét đứt trong hình vẽ thể hiện điều gì?
| Phần không tồn tại | |
| Phần thấy được | |
| Phần không thấy được | |
| Phần bị ẩn |
Lớp 12A4 có $32$ học sinh. Để gọi tên trả bài, thầy Sĩ đã nhập tên của mỗi bạn vào phần mềm và xuất ngẫu nhiên tên của một bạn, mỗi cái tên chỉ nhập một lần. Để tăng xác suất gọi trúng tên bạn lớp trưởng lên $50\%$, thầy Sĩ cần nhập tên bạn lớp trưởng bao nhiêu lần?
| $31$ | |
| $32$ | |
| $62$ | |
| $64$ |
Trong một video đập heo cuối năm, Lâm Vlog đã đặt $10$ triệu đồng tiền mặt vào chín trong số $10$ con heo đất. Bạn Ân được chọn một trong $10$ con heo đất để đập, xác suất đập trúng $10$ triệu của Ân là
| $\dfrac{1}{10}$ | |
| $0$ | |
| $\dfrac{9}{10}$ | |
| $\dfrac{1}{2}$ |
Bạn Ngân uống trà sữa nhân ngày khai trương quán Hỏa Mộc, được tham gia vòng quay may mắn. Vòng quay gồm có ô "trà sữa", "trà đào", "trà chanh", "trà khổ qua"; hỏi phép thử vòng quay may mắn này có không gian mẫu gồm bao nhiêu phần tử?
| $5$ | |
| $4$ | |
| $3$ | |
| Vô số |
Cho tập hợp $A$ có $10$ phần tử. Số tập con của $A$ là
| $11$ | |
| $1024$ | |
| $2048$ | |
| $12$ |
Tìm số hạng không chứa $x$ trong khải triển $\left(x^2-\dfrac{2}{x}\right)^6$.
| $2^4\mathrm{C}_6^2$ | |
| $2^2\mathrm{C}_6^2$ | |
| $-2^4\mathrm{C}_6^4$ | |
| $-2^2\mathrm{C}_6^4$ |
Biết rằng $(2x-3)^4=16x^4-96x^3+216x^2-216x+81$. Phát biểu nào sau đây không đúng?
| Số hạng thứ $4$ là $-216x$ | |
| Hệ số của $x^2$ là $216$ | |
| Hệ số của $x^3$ là $-96$ | |
| Tổng các hệ số của khai triển bằng $-1$ |
Khai triển biểu thức $(x+y)^2$ ta được
| $x^2+2xy+y^2$ | |
| $x^2-2xy+y^2$ | |
| $x^2+3xy+y^2$ | |
| $x^2-3xy+y^2$ |
Khối 11 trường THCS-THPT Mỹ Thuận có $13$ học sinh giỏi Toán, trong đó có $8$ học sinh nam và $5$ học sinh nữ. Nhà trường muốn chọn ra $4$ em trong số đó để tham dự Câu lạc bộ Toán học huyện Bình Tân, trong đó có nhiều nhất $2$ học sinh nữ. Hỏi có bao nhiêu cách chọn?
| $280$ | |
| $1120$ | |
| $630$ | |
| $365$ |
Khối 11 trường THCS-THPT Mỹ Thuận có $13$ học sinh giỏi Toán, trong đó có $8$ học sinh nam và $5$ học sinh nữ. Nhà trường muốn chọn ra $4$ em trong số đó để tham dự Câu lạc bộ Toán học huyện Bình Tân, trong đó có ít nhất $2$ học sinh nữ. Hỏi có bao nhiêu cách chọn?
| $280$ | |
| $1120$ | |
| $630$ | |
| $365$ |
Khối 11 trường THCS-THPT Mỹ Thuận có $13$ học sinh giỏi Toán, trong đó có $8$ học sinh nam và $5$ học sinh nữ. Nhà trường muốn chọn ra $4$ em trong số đó để tham dự Câu lạc bộ Toán học huyện Bình Tân, trong đó có $2$ học sinh nữ. Hỏi có bao nhiêu cách chọn?
| $280$ | |
| $1120$ | |
| $630$ | |
| $365$ |
