Cho khối lập phương có cạnh bằng \(6\). Thể tích khối lập phương đã cho bằng

	\(216\)
	\(18\)
	\(36\)
	\(72\)

Cho hai số phức \(z_1=-3+i\) và \(z_2=1-i\). Phần ảo của số phức \(z_1+\overline{z_2}\) bằng

	\(-2\)
	\(2i\)
	\(2\)
	\(-2i\)

Môđun của số phức \(1+2i\) bằng

	\(5\)
	\(\sqrt{3}\)
	\(\sqrt{5}\)
	\(3\)

Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(z=\left(1+2i\right)^2\) là điểm nào dưới đây?

	\(P\left(-3;4\right)\)
	\(Q\left(5;4\right)\)
	\(N\left(4;-3\right)\)
	\(M\left(4;5\right)\)

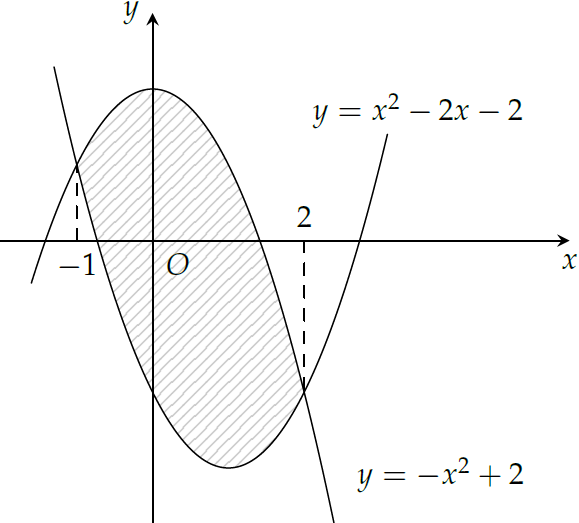
Diện tích phần hình phẳng được gạch chéo trong hình bên bằng

	\(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2+2x+4\right)\mathrm{\,d}x}\)
	\(\displaystyle\int\limits_{-1}^{2}{\left(2x^2-2x-4\right)\mathrm{\,d}x}\)
	\(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2-2x+4\right)\mathrm{\,d}x}\)
	\(\displaystyle\int\limits_{-1}^{2}{\left(2x^2+2x-4\right)\mathrm{\,d}x}\)

Cho hàm số \(f\left(x\right)\) có \(f\left(3\right)=3\) và \(f'\left(x\right)=\dfrac{x}{x+1-\sqrt{x+1}}\), \(\forall x>0\). Khi đó \(\displaystyle\int\limits_3^8f\left(x\right)\mathrm{\,d}x\) bằng

	\(7\)
	\(\dfrac{197}{6}\)
	\(\dfrac{29}{2}\)
	\(\dfrac{181}{6}\)

Nếu \(\displaystyle\int\limits_1^2f(x)\mathrm{\,d}x=-2\) và \(\displaystyle\int\limits_2^3f(x)\mathrm{\,d}x=1\) thì \(\displaystyle\int\limits_1^3f(x)\mathrm{\,d}x\) bằng

	\(-3\)
	\(-1\)
	\(1\)
	\(3\)

Họ tất cả các nguyên hàm của hàm số \(f\left(x\right)=\dfrac{x+2}{x-1}\) trên khoảng \(\left(1;+\infty\right)\) là

	\(x+3\ln\left(x-1\right)+C\)
	\(x-3\ln\left(x-1\right)+C\)
	\(x+\dfrac{3}{\left(x-1\right)^2}+C\)
	\(x-\dfrac{3}{\left(x-1\right)^2}+C\)

Họ tất cả các nguyên hàm của hàm số \(f(x)=\cos x+6x\) là

	\(\sin x+3x^2+C\)
	\(-\sin x+3x^2+C\)
	\(\sin x+6x^2+C\)
	\(-\sin x+C\)

Tập nghiệm của bất phương trình \(5^{x-1}\geq5^{x^2-x-9}\) là

	\(\left[-2;4\right]\)
	\(\left[-4;2\right]\)
	\(\left(-\infty;-2\right]\cup\left[4;+\infty\right)\)
	\(\left(-\infty;-4\right]\cup\left[2;+\infty\right)\)

Để dự báo dân số của một quốc gia, người ta sử dụng công thức \(S=A\mathrm{e}^{nr}\); trong đó \(A\) là dân số của năm lấy làm mốc tính, \(S\) là dân số sau \(n\) năm, \(r\) là tỉ lệ tăng dân số hàng năm. Năm \(2017\), dân số Việt Nam là \(93.671.600\) người (Tổng cục Thống kê, Niên giám Thống kê năm \(2017\), Nhà xuất bản Thống kê, Tr. \(79\)). Giả sử tỉ lệ tăng dân số hàng năm không đổi là \(0,81\%\) dự báo dân số Việt Nam năm \(2035\) là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)?

	\(109.256.100\)
	\(108.374.700\)
	\(107.500.500\)
	\(108.311.100\)

Xét tất cả các số thực dương \(a\) và \(b\) thỏa mãn $$\log_2a=\log_8\left(ab\right).$$Mệnh đề nào dưới đây đúng?

	\(a=b^2\)
	\(a^3=b\)
	\(a=b\)
	\(a^2=b\)

Với \(a\) là số thực dương tùy ý, \(\log_2\left(a^2\right)\) bằng

	\(2+\log_2a\)
	\(\dfrac{1}{2}+\log_2a\)
	\(2\log_2a\)
	\(\dfrac{1}{2}\log_2a\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

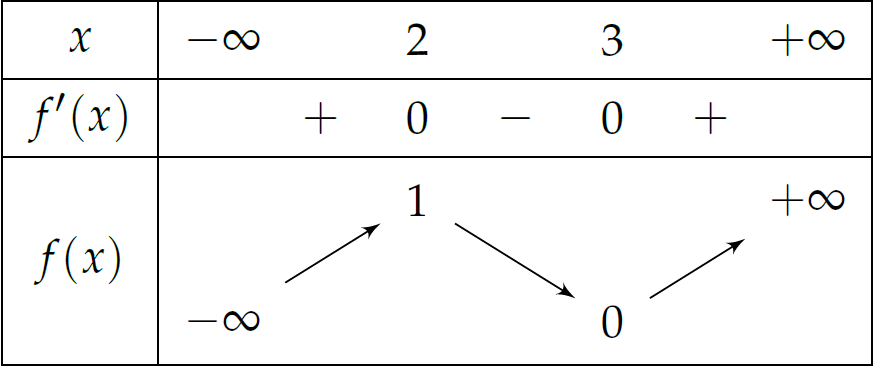
Số nghiệm thực của phương trình \(3f\left(x\right)-2=0\) là

	\(2\)
	\(0\)
	\(3\)
	\(1\)

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{5x^2-4x-1}{x^2-1}\) là

	\(1\)
	\(0\)
	\(2\)
	\(3\)

Giá trị lớn nhất của hàm số \(f\left(x\right)=-x^4+12x^2+1\) trên đoạn \(\left[-1;2\right]\) bằng

	\(1\)
	\(37\)
	\(33\)
	\(12\)

Cho hàm số \(f\left(x\right)\), bảng xét dấu của \(f'\left(x\right)\) như sau:

Số điểm cực trị của hàm số đã cho là

	\(0\)
	\(2\)
	\(1\)
	\(3\)

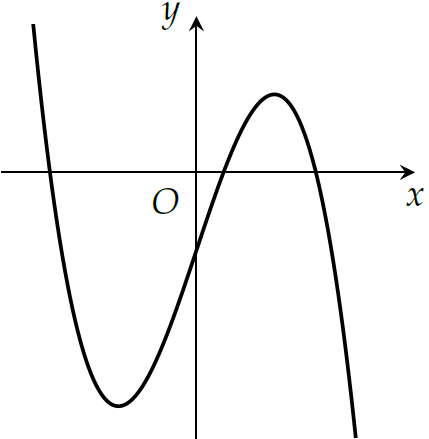
Cho hàm số \(y=ax^3+3x+d\) (\(a,\,d\in\mathbb{R}\)) có đồ thị như hình trên. Mệnh đề nào dưới đây đúng?

	\(a>0;\,d>0\)
	\(a<0;\,d>0\)
	\(a>0;\,d<0\)
	\(a<0;\,d<0\)

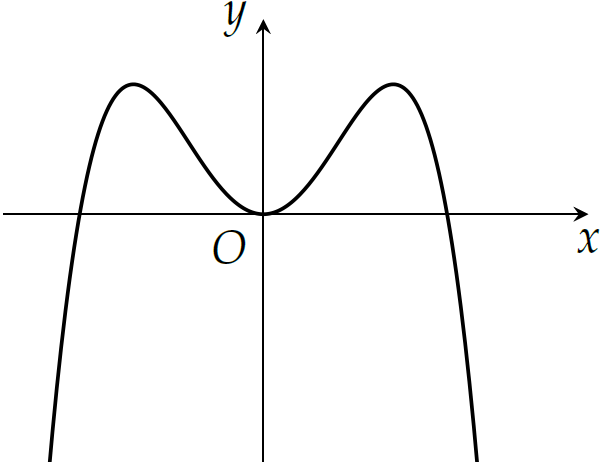
Đồ thị của hàm số nào sau đây có dạng như hình cong trong hình bên?

	\(y=-x^4+2x^2\)
	\(y=x^4-2x^2\)
	\(y=x^3-3x^2\)
	\(y=-x^3+3x^2\)

Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:

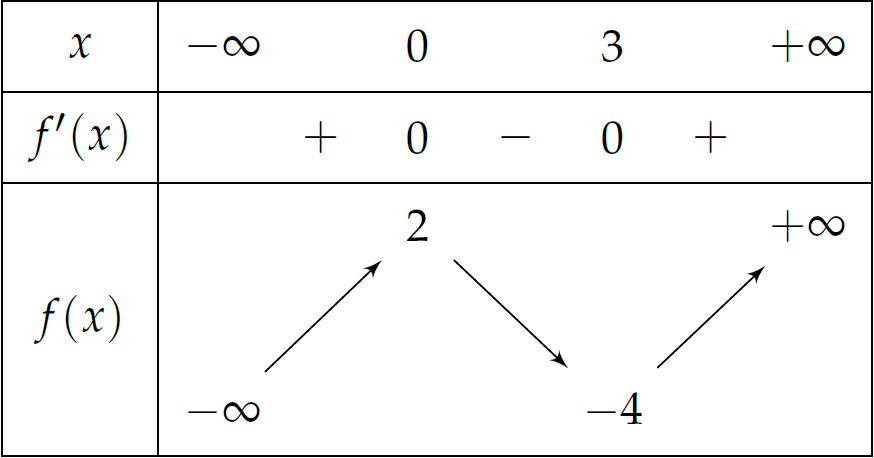
Giá trị cực tiểu của hàm số đã cho bằng

	\(2\)
	\(3\)
	\(0\)
	\(-4\)