Cho bảng biến thiên của hàm số \(y=f(x)\) như hình.
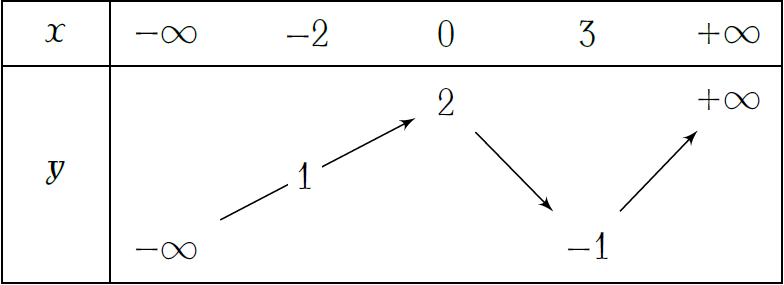
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số trên đoạn \([-2;3]\).
| \(\begin{cases}M=3\\ m=-2\end{cases}\) | |
| \(\begin{cases}M=0\\ m=3\end{cases}\) | |
| \(\begin{cases}M=2\\ m=-1\end{cases}\) | |
| \(\begin{cases}M=1\\ m=-1\end{cases}\) |
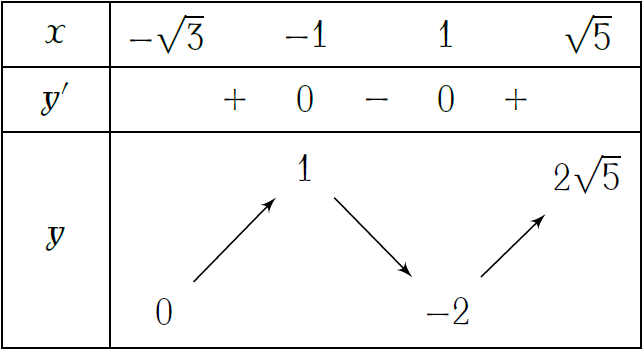
Cho hàm số \(y=f(x)\) xác định trên đoạn \(\left[-\sqrt{3};\sqrt{5}\right]\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
| \(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=0\) | |
| \(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\) | |
| \(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\sqrt{5}\) | |
| \(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\) |
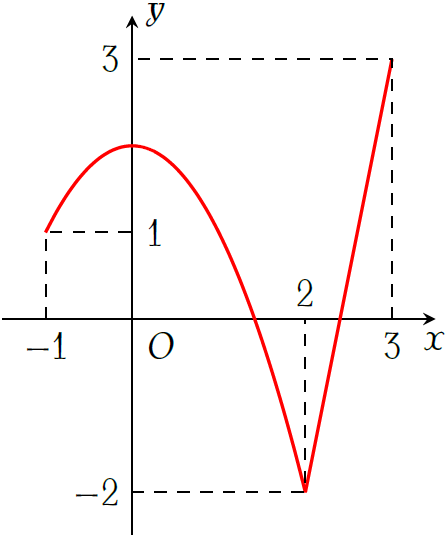
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \([-1;3]\). Giá trị của \(M-m\) bằng
| \(0\) | |
| \(1\) | |
| \(4\) | |
| \(5\) |
Tìm giá trị lớn nhất \(M\) của hàm số $$y=4\sin2x-3\cos2x.$$
| \(M=3\) | |
| \(M=1\) | |
| \(M=5\) | |
| \(M=4\) |
Tìm tập giá trị \(T\) của hàm số $$y=12\sin x-5\cos x.$$
| \(T=[-1;1]\) | |
| \(T=[-7;7]\) | |
| \(T=[-13;13]\) | |
| \(T=[-17;17]\) |
Tìm giá trị lớn nhất \(M\) của hàm số $$y=\dfrac{2}{1+\tan^2x}.$$
| \(M=\dfrac{1}{2}\) | |
| \(M=\dfrac{2}{3}\) | |
| \(M=1\) | |
| \(M=2\) |
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số $$y=\sin^2x+2\cos^2x.$$
| \(M=3,\,m=0\) | |
| \(M=2,\,m=0\) | |
| \(M=2,\,m=1\) | |
| \(M=3,\,m=1\) |
Tìm giá trị nhỏ nhất \(m\) của hàm số $$y=\dfrac{1}{\cos x+1}.$$
| \(m=\dfrac{1}{2}\) | |
| \(m=\dfrac{1}{\sqrt{2}}\) | |
| \(m=1\) | |
| \(m=\sqrt{2}\) |
Tìm tập giá trị \(T\) của hàm số $$y=\sin2019x-\cos2019x.$$
| \(T=[-2;2]\) | |
| \(T=[-4038;4038]\) | |
| \(T=\left[-\sqrt{2};\sqrt{2}\right]\) | |
| \(T=\left[0;\sqrt{2}\right]\) |
Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x+\cos x\). Tính \(P=M-m\).
| \(P=4\) | |
| \(P=2\sqrt{2}\) | |
| \(P=\sqrt{2}\) | |
| \(P=2\) |
Hàm số \(y=5+4\sin2x\cos2x\) có tất cả bao nhiêu giá trị nguyên?
| \(3\) | |
| \(4\) | |
| \(5\) | |
| \(6\) |
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y=1-2\left|\cos3x\right|\).
| \(M=3,\,m=-1\) | |
| \(M=1,\,m=-1\) | |
| \(M=2,\,m=-2\) | |
| \(M=0,\,m=-2\) |
Cho hàm số \(y=-2\sin\left(x+\dfrac{\pi}{3}\right)+2\). Mệnh đề nào sau đây là đúng?
| \(y\geq-4,\,\forall x\in\mathbb{R}\) | |
| \(y\geq4,\,\forall x\in\mathbb{R}\) | |
| \(y\geq0,\,\forall x\in\mathbb{R}\) | |
| \(y\geq2,\,\forall x\in\mathbb{R}\) |
Tìm giá trị nhỏ nhất \(m\) của hàm số $$y=-\sqrt{2}\sin\left(2019x+2020\right).$$
| \(m=-2019\sqrt{2}\) | |
| \(m=-\sqrt{2}\) | |
| \(m=-1\) | |
| \(m=\sqrt{2}\) |
Tìm tập giá trị \(T\) của hàm số \(y=5-3\sin x\).
| \(T=[-1;1]\) | |
| \(T=[-3;3]\) | |
| \(T=[2;8]\) | |
| \(T=[5;8]\) |
Tìm tập giá trị \(T\) của hàm số \(y=3\cos2x+5\).
| \(T=[-1;1]\) | |
| \(T=[-1;11]\) | |
| \(T=[2;8]\) | |
| \(T=[5;8]\) |
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y=3\sin x-2\).
| \(M=1,\,m=-5\) | |
| \(M=3,\,m=1\) | |
| \(M=2,\,m=-2\) | |
| \(M=0,\,m=-2\) |
Cho hàm số \(f\left(x\right)=\dfrac{x+m}{x+1}\) (\(m\) là tham số thực). Gọi \(S\) là tập hợp tất cả các giá trị của m sao cho $$\max\limits_{[0;1]}\left|f\left(x\right)\right|+\min\limits_{[0;1]}\left|f\left(x\right)\right|=2.$$Số phần tử của \(S\) là
| \(6\) | |
| \(2\) | |
| \(1\) | |
| \(4\) |
Xét các số thực dương \(a,\,b,\,x,\,y\) thỏa mãn \(a>1,\,b>1\) và \(a^x=b^y=\sqrt{ab}\). Giá trị nhỏ nhất của biểu thức \(P=x+2y\) thuộc tập hợp nào dưới đây?
| \(\left(1;2\right)\) | |
| \(\left[2;\dfrac{5}{2}\right)\) | |
| \(\left[3;4\right)\) | |
| \(\left[\dfrac{5}{2};3\right)\) |
Giá trị nhỏ nhất của hàm số \(y=x^4-10x^2+2\) trên đoạn \(\left[-1;2\right]\) bằng
| \(2\) | |
| \(-23\) | |
| \(-22\) | |
| \(-7\) |
