Kết quả của $\lim\limits_{x\rightarrow2}\dfrac{x^2-4}{x-2}$ bằng
| $+\infty$ | |
| $-\infty$ | |
| $0$ | |
| $4$ |
Hàm số $y=\dfrac{x^2-4x+3}{x+1}$ không liên tục tại điểm nào sau đây?
| $x=1$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-1$ |
Giới hạn $\lim\dfrac{2022}{n}$ bằng
| $0$ | |
| $+\infty$ | |
| $2022$ | |
| $1$ |
Giới hạn $\lim\limits_{x\rightarrow+\infty}\left(x^4-4x^2+3\right)$ là
| $+\infty$ | |
| $3$ | |
| $-\infty$ | |
| $1$ |
Kết quả của $S=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^n}+\cdots$ là
| $\dfrac{1}{2}$ | |
| $1$ | |
| $+\infty$ | |
| $0$ |
Biết rằng khi $m=m_0$ thì $\lim\limits_{x\rightarrow2}\dfrac{x^2+mx+2}{x-2}=1$. Số $m_0$ thuộc khoảng nào sau đây?
| $(-2;0)$ | |
| $(0;2)$ | |
| $(-4;-2)$ | |
| $(2;4)$ |
$\lim\limits_{x\rightarrow-\infty}\dfrac{3x-1}{2x+3}$ bằng bao nhiêu?
| $-3$ | |
| $\dfrac{3}{2}$ | |
| $-\dfrac{1}{3}$ | |
| $\dfrac{2}{3}$ |
Giá trị của $\lim\limits_{x\rightarrow-1}(4-3x)$ bằng
| $-7$ | |
| $-1$ | |
| $7$ | |
| $1$ |
Cho hàm số $f(x)=\begin{cases}\dfrac{4x^2+3x-1}{x+1} &\text { khi }x\neq-1\\ 2m+1 &\text { khi }x=-1\end{cases}$. Với giá trị nào của $m$ thì hàm số đã cho liên tục tại điểm $x=-1$?
| $m=2$ | |
| $m=-3$ | |
| $m=\dfrac{1}{2}$ | |
| $m=0$ |
Cho hàm số $y=f(x)$ có đồ thị được biểu diễn trong hệ trục tọa độ $Oxy$ như hình vẽ bên.
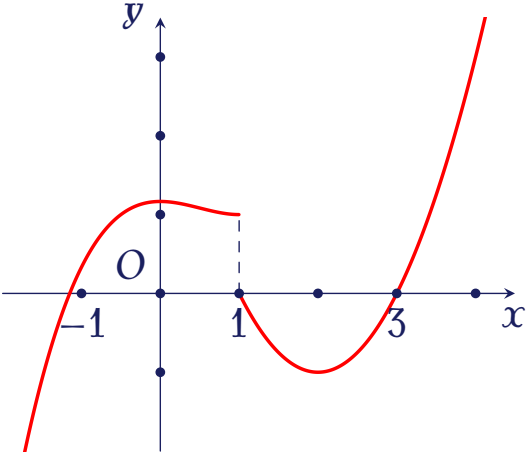
Mệnh đề nào sau đây sai?
| Hàm số $y=f(x)$ liên tục tại điểm $x=3$ | |
| Hàm số $y=f(x)$ liên tục tại điểm $x=-1$ | |
| Hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ | |
| Hàm số $y=f(x)$ gián đoạn tại điểm $x=1$ |
Giá trị thực của tham số $m$ để hàm số $f\left(x\right)=\begin{cases}2x+1 &\text{khi }x\ge2\\ m &\text{khi }x< 2\end{cases}$ liên tục tại $x=2$ bằng
| $5$ | |
| $2$ | |
| $3$ | |
| $1$ |
Cho $\left(u_n\right)$ là cấp số nhân với $u_1=3$ và công bội $q=\dfrac{1}{2}$. Gọi $S_n$ là tổng của $n$ số hạng đầu tiên của cấp số nhân đã cho. Ta có $\lim S_n$ bằng
| $6$ | |
| $\dfrac{3}{2}$ | |
| $3$ | |
| $\dfrac{1}{2}$ |
$\lim\limits_{x\to0}\dfrac{\sin x}{x}$ bằng
| $1$ | |
| $-1$ | |
| $0$ | |
| $+\infty$ |
$\lim\limits_{x\to+\infty}\left(2x+3\right)$ bằng
| $+\infty$ | |
| $2$ | |
| $3$ | |
| $-\infty$ |
$\lim\limits_{x\to2}\left(x^2-1\right)$ bằng
| $3$ | |
| $-1$ | |
| $1$ | |
| $+\infty$ |
$\lim\left(\dfrac{1}{3}\right)^n$ bằng
| $0$ | |
| $\dfrac{1}{3}$ | |
| $1$ | |
| $+\infty$ |
$\lim\dfrac{1}{2n+1}$ bằng
| $0$ | |
| $\dfrac{1}{2}$ | |
| $1$ | |
| $+\infty$ |
Cho hai dãy $\left(u_n\right)$ và $\left(v_n\right)$ thỏa mãn $\lim u_n=2$ và $\lim v_n=3$. Giá trị của $\lim\left(u_n+v_n\right)$ bằng
| $5$ | |
| $6$ | |
| $-1$ | |
| $1$ |
Giới hạn \(\lim\limits_{x\to1}\dfrac{2x-7}{x-1}\) bằng
| \(\dfrac{9}{2}\) | |
| \(-\infty\) | |
| \(+\infty\) | |
| Không tồn tại |
Giới hạn \(\lim\limits_{x\to1^-}\dfrac{2x-7}{x-1}\) bằng
| \(0\) | |
| \(\dfrac{9}{2}\) | |
| \(+\infty\) | |
| \(-\infty\) |
