Cho hai tập hợp \(A=\{1;2;5;7\}\) và \(B=\{1;2;3\}\). Có tất cả bao nhiêu tập hợp \(X\) sao cho \(X\subset A\) và \(X\subset B\)?

	\(1\)
	\(2\)
	\(3\)
	\(4\)

Cho hai tập hợp \(A=\{1;2;3\}\) và \(B=\{1;2;3;4;5\}\). Có tất cả bao nhiêu tập \(X\) sao cho \(A\subset X\subset B\)?

	\(4\)
	\(5\)
	\(6\)
	\(8\)

Tập hợp nào sau đây có đúng hai tập con?

	\(\{x;\,y\}\)
	\(\{x\}\)
	\(\{\varnothing;\,x\}\)
	\(\{\varnothing;\,x;\,y\}\)

Tập hợp nào sau đây có đúng một tập con?

	\(\varnothing\)
	\(\{1\}\)
	\(\{\varnothing\}\)
	\(\{\varnothing;1\}\)

Tập hợp \(X=\{0;2;4;6\}\) có bao nhiêu tập con gồm \(2\) phần tử?

	\(4\)
	\(6\)
	\(7\)
	\(8\)

Cho tập hợp \(X=\{1;2;3;4\}\). Khẳng định nào sau đây đúng?

	\(X\) có \(16\) tập con
	\(X\) có \(8\) tập con gồm \(2\) phần tử
	\(X\) có \(16\) tập con chứa số \(1\)
	\(X\) không có tập con nào chứa \(4\) phần tử

Cho tập hợp \(X=\{2;3;4\}\). Hỏi \(X\) có bao nhiêu tập con?

	\(3\)
	\(6\)
	\(8\)
	\(9\)

Tập hợp \(B=\{a;b;c;d;e;f\}\) có bao nhiêu tập con?

	\(36\)
	\(7\)
	\(32\)
	\(64\)

Cho tập hợp $A$ có $7$ phần tử. Số tập con gồm $3$ phần tử của tập hợp $A$ là

	$\mathrm{A}_7^3$
	$3^7$
	$\mathrm{C}_7^3$
	$7^3$

Cho tập hợp $A$ có $15$ phần tử. Số tập con gồm hai phần tử của $A$ bằng

	$225$
	$30$
	$210$
	$105$

Cho các tập hợp

• \(M=\{x\in\mathbb{N}^*\colon x\text{ là bội của }2\}\),
• \(N=\{x\in\mathbb{N}^*\colon x\text{ là bội của }6\}\),
• \(P=\{x\in\mathbb{N}\colon x\text{ là ước của }2\}\),
• \(Q=\{x\in\mathbb{N}\colon x\text{ là ước của }6\}\).

Mệnh đề nào sau đây đúng?

	\(M\subset N\)
	\(Q\subset P\)
	\(M\cap N=N\)
	\(P\cap Q=Q\)

Mệnh đề nào sau đây sai?

	\(A\cap B=A\Leftrightarrow A\subset B\)
	\(A\cup B=A\Leftrightarrow B\subset A\)
	\(A\setminus B=A\Leftrightarrow A\cap B=\varnothing\)
	\(A\setminus B=\varnothing\Leftrightarrow A\cap B=\varnothing\)

Cho hai tập hợp \(M,\,N\) sao cho \(M\subset N\). Mệnh đề nào sau đây đúng?

	\(M\cap N=N\)
	\(M\setminus N=N\)
	\(M\cap N=M\)
	\(M\setminus N=M\)

Cho \(M,\,N\) là hai tập hợp khác rỗng. Mệnh đề nào sau đây đúng?

	\(M\setminus N\subset N\)
	\(M\setminus N\subset M\)
	\(\left(M\setminus N\right)\cap N\neq\varnothing\)
	\(M\setminus N\subset M\cap N\)

Cho \(x\) là một phần tử của tập hợp \(A\). Xét các mệnh đề sau:

1. \(x\in A\)
2. \(\{x\}\in A\)
3. \(x\subset A\)
4. \(\{x\}\subset A\)

Trong các mệnh đề trên, mệnh đề nào đúng?

	I và II
	I và III
	I và IV
	II và IV

Cho \(A\) là một tập hợp. Trong các mệnh đề sau, mệnh đề nào đúng?

	\(A\in A\)
	\(\varnothing\in A\)
	\(A\subset A\)
	\(A\in\{A\}\)

Hình nào sau đây minh họa tập \(A\) là tập con của tập \(B\)?

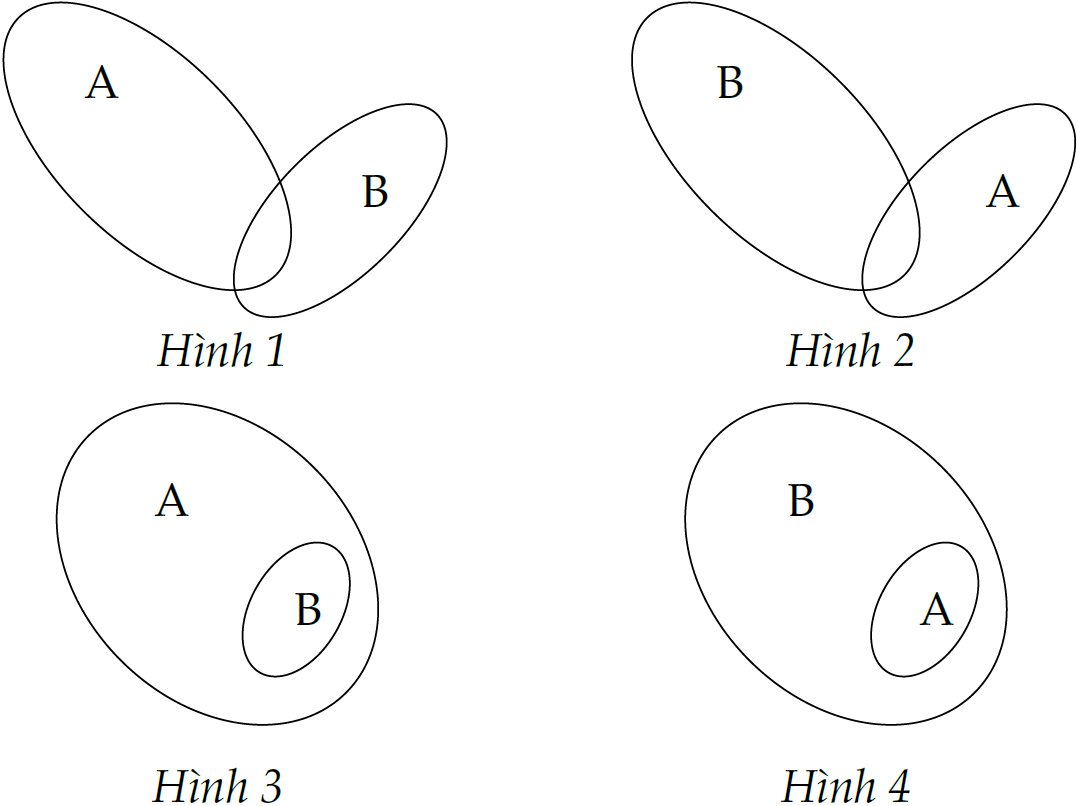
	Hình 1
	Hình 2
	Hình 3
	Hình 4

Kí hiệu nào sau đây dùng để viết đúng mệnh đề "\(7\) là số tự nhiên"?

	\(7\subset\mathbb{N}\)
	\(7\in\mathbb{N}\)
	\(7\notin\mathbb{N}\)
	\(7\leq\mathbb{N}\)

Gọi \(S\) là tập nghiệm của bất phương trình \(x^2-8x+7\geq0\). Trong các tập hợp sau, tập nào không phải lập con của \(S\)?

	\([8;+\infty)\)
	\((-\infty;-1]\)
	\((-\infty;0]\)
	\([6;+\infty)\)

Biết số phức $z$ thỏa mãn $\big|\overline{z}-3-2i\big|=\sqrt{5}$ và tập hợp các điểm biểu diễn số phức $w=(1-i)z+2$ là một đường tròn. Xác định tâm $I$ và bán kính của đường tròn đó.

	$I(-3;-5)$, $R=\sqrt{5}$
	$I(3;-5)$, $R=\sqrt{10}$
	$I(-3;5)$, $R=\sqrt{10}$
	$I(3;5)$, $R=10$