Một túi có $20$ viên bi khác nhau trong đó có $7$ viên bi đỏ, $8$ viên bi xanh và $5$ viên bi vàng. Số cách lấy hai viên bi khác màu là
| $40$ | |
| $78400$ | |
| $131$ | |
| $2340$ |
Một túi có $20$ viên bi khác nhau trong đó có $7$ viên bi đỏ, $8$ viên bi xanh và $5$ viên bi vàng. Số cách lấy ba viên bi khác màu là
| $20$ | |
| $280$ | |
| $6840$ | |
| $1140$ |
Một lớp có $23$ học sinh nữ và $17$ học sinh nam. Có bao nhiêu cách chọn hai học sinh tham gia hội trại với điều kiện có cả nam và nữ tham gia?
| $23$ | |
| $17$ | |
| $40$ | |
| $391$ |
Một lớp có $23$ học sinh nữ và $17$ học sinh nam. Có bao nhiêu cách chọn một học sinh tham gia cuộc thi tìm hiểu môi trường?
| $23$ | |
| $17$ | |
| $40$ | |
| $391$ |
Trong một video đập heo cuối năm, Lâm Vlog đã đặt $10$ triệu đồng tiền mặt vào một trong $10$ con heo đất, trong đó có $6$ con heo cỡ nhỏ và $4$ con heo cỡ lớn. Bạn Ân được chọn một con cỡ nhỏ và một con cỡ lớn trong số đó để đập, hỏi Ân có bao nhiêu cách chọn?
| $10$ | |
| $6$ | |
| $4$ | |
| $24$ |
Trong một video đập heo cuối năm, Lâm Vlog đã đặt $10$ triệu đồng tiền mặt vào một trong $10$ con heo đất, trong đó có $6$ con heo cỡ nhỏ và $4$ con heo cỡ lớn. Bạn Ân được chọn một con trong số đó để đập, hỏi Ân có bao nhiêu cách chọn?
| $10$ | |
| $6$ | |
| $4$ | |
| $24$ |
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y=\big|x^4-2mx^2+64x\big|$ có đúng ba điểm cực trị?
| $5$ | |
| $6$ | |
| $12$ | |
| $11$ |
Trong không gian $Oxyz$, cho mặt cầu $(S)$ tâm $I(1;3;9)$ bán kính bằng $3$. Gọi $M,\,N$ là hai điểm lần lượt thuộc hai trục $Ox$, $Oz$ sao cho đường thẳng $MN$ tiếp xúc với $(S)$, đồng thời mặt cầu ngoại tiếp tứ diện $OIMN$ có bán kính bằng $\dfrac{13}{2}$. Gọi $A$ là tiếp điểm của $MN$ và $(S)$, giá trị $AM\cdot AN$ bằng
| $39$ | |
| $12\sqrt{3}$ | |
| $18$ | |
| $28\sqrt{3}$ |
Có bao nhiêu số phức $z$ thỏa mãn $\big|z^2\big|=2\big|z-\overline{z}\big|$ và $\left|(z-4)\big(\overline{z}-4i\big)\right|=|z+4i|^2$?
| $3$ | |
| $1$ | |
| $2$ | |
| $4$ |
Cho hàm số bậc bốn $y=f(x)$. Biết rằng hàm số $g(x)=\ln f(x)$ có bảng biến thiên như sau:
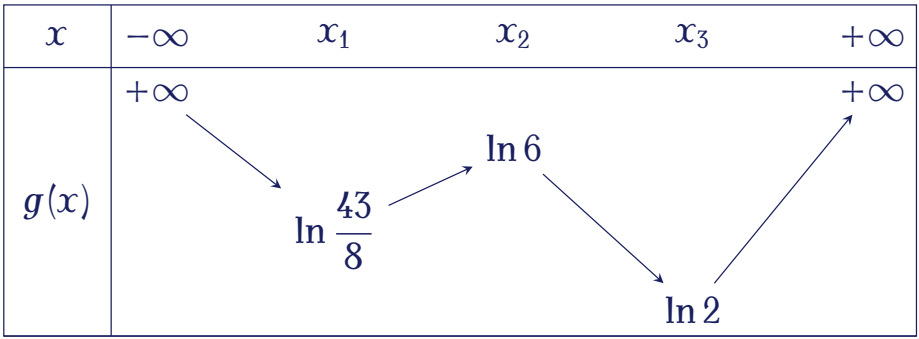
Diện tích hình phẳng giới hạn bởi các đường $y=f'(x)$ và $y=g'(x)$ thuộc khoảng nào dưới đây?
| $(5;6)$ | |
| $(4;5)$ | |
| $(2;3)$ | |
| $(3;4)$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=2a$. Góc giữa đường thẳng $BC'$ và mặt phẳng $(ACC'A')$ bằng $30^\circ$. Thể tích của khối lăng trụ đã cho bằng
| $3a^3$ | |
| $a^3$ | |
| $12\sqrt{2}a^3$ | |
| $4\sqrt{2}a^3$ |
Cho các số phức $z_1,\,z_2,\,z_3$ thỏa mãn $\big|z_1\big|=\big|z_2\big|=2\big|z_3\big|=2$ và $8\big(z_1+z_2\big)z_3=3z_1z_2$. Gọi $A,\,B,\,C$ lần lượt là các điểm biểu diễn của $z_1,\,z_2,\,z_3$ trên mặt phẳng tọa độ. Diện tích tam giác $ABC$ bằng
| $\dfrac{\sqrt{55}}{32}$ | |
| $\dfrac{\sqrt{55}}{16}$ | |
| $\dfrac{\sqrt{55}}{24}$ | |
| $\dfrac{\sqrt{55}}{8}$ |
Xét tất cả các số thực $x,\,y$ sao cho $a^{4x-\log_5a^2}\leq25^{40-y^2}$ với mọi số thực dương $a$. Giá trị lớn nhất của biểu thức $P=x^2+y^2+x-3y$ bằng
| $\dfrac{125}{2}$ | |
| $80$ | |
| $60$ | |
| $20$ |
Cho hình nón có góc ở đỉnh bằng $120^\circ$ và chiều cao bằng $4$. Gọi $(S)$ là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của $(S)$ bằng
| $64\pi$ | |
| $256\pi$ | |
| $192\pi$ | |
| $96\pi$ |
Trong không gian $Oxyz$, cho điểm $A(1;2;-2)$. Gọi $(P)$ là mặt phẳng chứa trục $Ox$ sao cho khoảng cách từ $A$ đến $(P)$ lớn nhất. Phương trình của $(P)$ là
| $2y+z=0$ | |
| $2y-z=0$ | |
| $y+z=0$ | |
| $y-z=0$ |
Biết $F(x)$ và $G(x)$ là hai nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$ và $\displaystyle\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=F(3)-G(0)+a$ ($a>0$). Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=F(x)$, $y=G(x)$, $x=0$ và $x=3$. Khi $S=15$ thì $a$ bằng
| $15$ | |
| $12$ | |
| $18$ | |
| $5$ |
Cho hàm số $f(x)=(m-1)x^4-2mx^2+1$ với $m$ là tham số thực. Nếu $\min\limits_{[0;3]}f(x)=f(2)$ thì $\max\limits_{[0;3]}f(x)$ bằng
| $-\dfrac{13}{3}$ | |
| $4$ | |
| $-\dfrac{14}{3}$ | |
| $1$ |
Có bao nhiêu số nguyên dương $a$ sao cho ứng với mỗi số $a$ có đúng ba số nguyên $b$ thỏa mãn $\big(3^b-3\big)\big(a\cdot2^b-18\big)< 0$?
| $72$ | |
| $73$ | |
| $71$ | |
| $74$ |
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn $[40;60]$. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
| $\dfrac{4}{7}$ | |
| $\dfrac{2}{5}$ | |
| $\dfrac{3}{5}$ | |
| $\dfrac{3}{7}$ |
Trong không gian $Oxyz$, cho điểm $A(0;-3;2)$ và mặt phẳng $(P)\colon2x-y+3z+5=0$. Mặt phẳng đi qua $A$ và song song với $(P)$ có phương trình là
| $2x-y+3z+9=0$ | |
| $2x+y+3z-3=0$ | |
| $2x+y+3z+3=0$ | |
| $2x-y+3z-9=0$ |
