Cho hai số thực $a,\,b>1$. Khẳng định nào dưới đây đúng?
| $\log(a+b)=\log a+\log b$ | |
| $\log(ab)=\log a+\log b$ | |
| $\log(a-b)=\log a-\log b$ | |
| $\log\left(\dfrac{a}{b}\right)=\log a+\log b$ |
Cho số thực $a>0$ và $a\neq1$, khi đó $\log_a\sqrt[3]{a}$ bằng
| $-\dfrac{1}{3}$ | |
| $\dfrac{1}{3}$ | |
| $-3$ | |
| $3$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho khối nón có diện tích đáy $B=a^2$ và chiều cao $h=3a$. Thể tích của khối nón bằng
| $a^3$ | |
| $3a^3$ | |
| $2a^3$ | |
| $4a^3$ |
Tập nghiệm của bất phương trình $3^x>5$ là
| $\big(0;\log_35\big)$ | |
| $\big(\log_53;+\infty\big)$ | |
| $\big(\log_35;+\infty\big)$ | |
| $\big(0;\log_53\big)$ |
Phương trình $3^{1-x}=9$ có nghiệm là
| $x=-1$ | |
| $x=-2$ | |
| $x=1$ | |
| $x=2$ |
Thể tích của khối lập phương cạnh $4a$ bằng
| $16a^3$ | |
| $36a^3$ | |
| $27a^3$ | |
| $64a^3$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,b,c\in\mathbb{R}$) có đồ thị như hình bên.
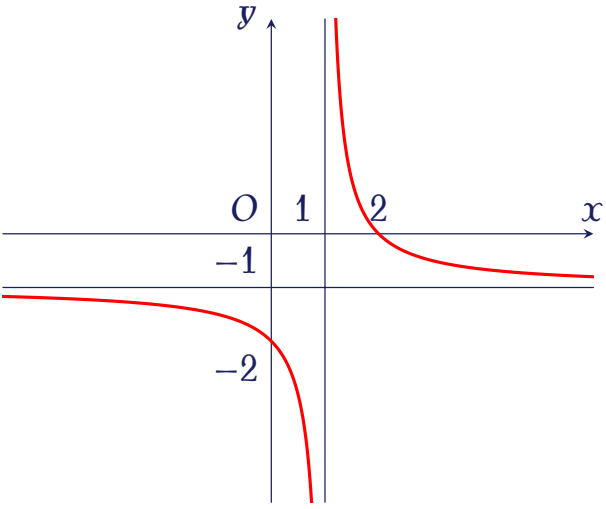
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Cho mặt cầu $\mathscr{S}(O,r)$, biết khoảng cách từ $O$ tới mặt phẳng $(P)$ bằng $\dfrac{r}{3}$. Mặt phẳng $(P)$ cắt mặt cầu theo một đường tròn có bán kính bằng
| $\dfrac{2r\sqrt{2}}{3}$ | |
| $r\sqrt{3}$ | |
| $\dfrac{2r}{3}$ | |
| $\dfrac{r\sqrt{3}}{3}$ |
Tập xác định của hàm số $y=\log_{\sqrt{3}}x$ là
| $[0;+\infty)$ | |
| $(0;+\infty)$ | |
| $(-\infty;0)$ | |
| $\mathbb{R}$ |
Tìm giá trị nhỏ nhất của hàm số $y=x+\dfrac{3}{x}-4$ trên đoạn $[1;5]$.
| $\dfrac{8}{5}$ | |
| $4-2\sqrt{3}$ | |
| $0$ | |
| $2\sqrt{3}-4$ |
Đồ thị của hàm số nào dưới đây cắt trục hoành tại $3$ điểm phân biệt?
| $y=x^3-3x+3$ | |
| $y=x^3+3x+1$ | |
| $y=-x^3+3x+5$ | |
| $y=x^3-3x+1$ |
Tìm giá trị nhỏ nhất của hàm số $y=2\sqrt{x+2}$ trên đoạn $[-1;3]$.
| $1$ | |
| $2$ | |
| $4$ | |
| $-1$ |
Cho tứ diện $ABCD$. Gọi $N,\,K$ lần lượt là trung điểm các cạnh $BC$ và $CD$, $M$ là điểm trên cạnh $AB$ sao cho $MB=2MA$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là
| Hình bình hành | |
| Hình thang | |
| Hình chữ nhật | |
| Hình thoi |
Cho tứ diện $ABCD$. Gọi $M,\,N,\,K$ lần lượt là trung điểm các cạnh $AB$, $BC$, $CD$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là
| Hình bình hành | |
| Hình thang | |
| Hình chữ nhật | |
| Hình thoi |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$ là đường thẳng
| Đi qua điểm $S$ và song song với $AD$ | |
| Đi qua điểm $S$ và song song với $AB$ | |
| Không tồn tại | |
| Đi qua giao điểm $I$ của $AB$ và $CD$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Phát biểu nào không đúng về giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$?
| Song song với $CD$ | |
| Đi qua điểm $S$ | |
| Song song với $AB$ | |
| Đi qua giao điểm $I$ của $AB$ và $CD$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$
| Không tồn tại | |
| Đi qua điểm $S$ | |
| Đi qua giao điểm $I$ của $AD$ và $BC$ | |
| Đi qua giao điểm $I$ của $AB$ và $CD$ |
