Gieo một đồng xu (cân đối và đồng chất) ba lần. Số phần tử của không gian mẫu là

	\(6\)
	\(3\)
	\(4\)
	\(8\)

Gieo một đồng xu (cân đối và đồng chất) liên tiếp hai lần. Tìm không gian mẫu \(\Omega\).

	\(\Omega=\left\{S;N\right\}\)
	\(\Omega=\left\{SN;NN;SS\right\}\)
	\(\Omega=\left\{SN;NS;SS;NN\right\}\)
	\(\Omega=\left\{SN;NS\right\}\)

Cho tứ diện \(ABCD\). Gọi \(M,\,K\) lần lượt là trung điểm của \(BC\) và \(AC\), \(N\) là điểm trên cạnh \(BD\) sao cho \(BN=2ND\). Gọi \(F\) là giao điểm của \(AD\) và \((MNK)\).

Trong các mệnh đề sau đây, mệnh đề nào đúng?

	\(AF=FD\)
	\(AF=3FD\)
	\(FD=2AF\)
	\(AF=2FD\)

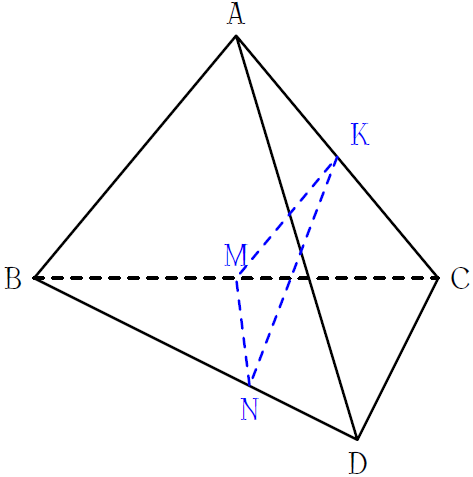
Cho tứ diện \(ABCD\). Gọi \(M,\,K\) lần lượt là trung điểm của \(BC\) và \(AC\), \(N\) là điểm trên cạnh \(BD\) sao cho \(BN=2ND\). Giao điểm của \(MN\) và \((ACD)\) là

	Giao điểm của \(MN\) với \(AD\)
	Giao điểm của \(MN\) với \(KD\)
	Giao điểm của \(MN\) với \(CD\)
	Không có

Trong các mệnh đề sau, mệnh đề nào đúng?

	Hai đường thẳng phân biệt không cắt nhau thì chéo nhau
	Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau
	Hai đường thẳng phân biệt không song song thì chéo nhau
	Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau

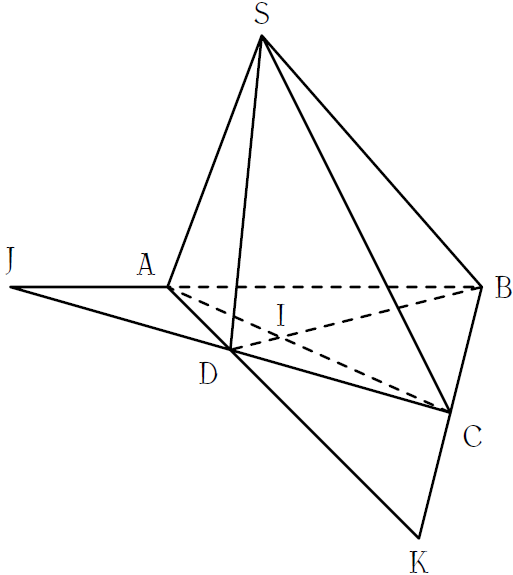
Cho hình chóp \(S.ABCD\). Gọi \(AC\cap BD={I}\), \(AB\cap CD={J}\), \(AD\cap BC={K}\). Đẳng thức nào sai trong các đẳng thức sau đây?

	\((SAC)\cap(SAD)=SB\)
	\((SAB)\cap(SCD)=SJ\)
	\((SAD)\cap(SBC)=SK\)
	\((SAC)\cap(SBD)=SI\)

Cho tứ diện \(ABCD\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(AD\) và \(BC\); \(G\) là trọng tâm tam giác \(BCD\).

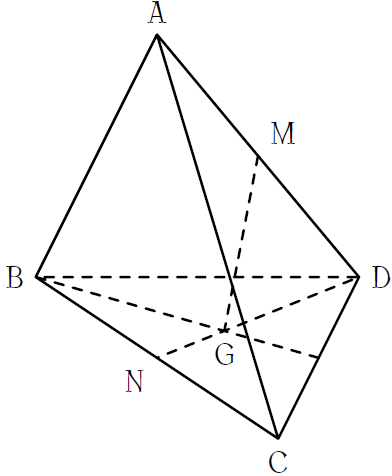
Khi ấy giao điểm của đường thẳng \(MG\) và mặt phẳng \((ABC)\) là

	Điểm \(C\)
	Điểm \(N\)
	Giao điểm của đường thẳng \(MG\) và đường thẳng \(BC\)
	Giao điểm của đường thẳng \(MG\) và đường thẳng \(AN\)

Tìm mệnh đề đúng trong các mệnh đề sau:

	Nếu hai mặt phẳng (\(\alpha\)) và (\(\beta\)) song song với nhau thì mọi đường thẳng nằm trong (\(\alpha\)) đều song song với mọi đường thẳng nằm trong (\(\beta\))
	Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt (\(\alpha\)) và (\(\beta\)) thì (\(\alpha\)) và (\(\beta\)) song song với nhau
	Nếu hai mặt phẳng (\(\alpha\)) và (\(\beta\)) song song với nhau thì mọi đường thẳng nằm trong (\(\alpha\)) đều song song với (\(\beta\))
	Qua một điểm nằm ngoài mặt phẳng cho trước ta sẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó

Tìm mệnh đề sai trong các mệnh đề sau đây:

	Nếu hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì chúng song song với nhau
	Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
	Nếu hai mặt phẳng có một điểm chung thì còn có vô số điểm chung khác nữa
	Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại

Trong mặt phẳng \(Oxy\) cho đường tròn \((x-8)^2+(y-3)^2=7\). Ảnh của đường tròn qua phép quay tâm \(O\) góc \(90^\circ\) là

	\((x+3)^2+(y-8)^2=4\)
	\((x+8)^2+(y-3)^2=7\)
	\((x+8)^2+(y+3)^2=7\)
	\((x+3)^2+(y-8)^2=7\)

Gọi \(N\) là ảnh của điểm \(M=\left(-6;1\right)\) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay \(\mathrm{Q}_{\left(O,90^\circ\right)}\) và phép vị tự tâm \(O\) tỉ số \(k=2\). Tọa độ điểm \(N\) là

	\(N=\left(-2;-12\right)\)
	\(N=\left(2;12\right)\)
	\(N=\left(-12;-2\right)\)
	\(N=\left(12;2\right)\)

Cho \(d\colon2x+y-3=0\). Phép vị tự tâm \(O\) tỉ số \(2\) biến đường thẳng \(d\) thành

	\(2x+y+3=0\)
	\(4x+2y-3=0\)
	\(2x+y-6=0\)
	\(4x+2y-5=0\)

Trong mặt phẳng \(Oxy\), ảnh của điểm \(M\left(-6;1\right)\) qua phép quay \(\mathrm{Q}_{\left(O,90^\circ\right)}\) là

	\(M'\left(1;6\right)\)
	\(M'\left(-1;-6\right)\)
	\(M'\left(-6;-1\right)\)
	\(M'\left(6;1\right)\)

Tìm ảnh của điểm \(M=(2;5)\) qua phép tịnh tiến theo vectơ \(\overrightarrow{u}=(-3;1)\).

	\(M'=\left(-1;6\right)\)
	\(M'=\left(-2;7\right)\)
	\(M'=\left(7;-2\right)\)
	\(M'=\left(-6;5\right)\)

Biểu thức tọa độ của phép quay \(\mathrm{Q}_{\left(O,-90^\circ\right)}\) là

	\(\begin{cases}x'=-y\\ y'=x\end{cases}\)
	\(\begin{cases}x'=x\\ y'=-y\end{cases}\)
	\(\begin{cases}x'=-x\\ y'=y\end{cases}\)
	\(\begin{cases}x'=y\\ y'=-x\end{cases}\)

Tìm số hạng chính giữa của khai triển \(\left(\sqrt[3]{x}+\dfrac{1}{\sqrt[4]{x}}\right)^8\),với \(x>0\).

	\(70x^{\tfrac{1}{3}}\) và \(56x^{-\tfrac{1}{4}}\)
	\(56x^{-\tfrac{1}{4}}\)
	\(70x^{\tfrac{1}{3}}\)
	\(70\sqrt[3]{x}\sqrt[4]{x}\)

Trong khai triển \(\left(x-\sqrt{y}\right)^{16}\), hai số hạng cuối là

	\(-16x\sqrt{y^{15}}+y^4\)
	\(-16x\sqrt{y^{15}}+y^8\)
	\(16xy^{15}+y^4\)
	\(16xy^{15}+y^8\)

Trong khai triển \(\left(a-\dfrac{5}{x^3}\right)^{2019}\) có bao nhiêu số hạng?

	\(2020\) số hạng
	\(2019\) số hạng
	\(2018\) số hạng
	\(2021\) số hạng

Trong khai triển \((2a-b)^5\) theo thứ tự mũ giảm dần của \(a\) thì \(80a^3b^2\) là số hạng thứ

	\(2\)
	\(4\)
	\(5\)
	\(3\)

Hệ số của \(x^5\) trong khai triển \((2x+3)^8\) là

	\(\mathrm{C}_8^3\cdot2^3\cdot3^5\)
	\(-\mathrm{C}_8^5\cdot2^5\cdot3^3\)
	\(\mathrm{C}_8^3\cdot2^5\cdot3^3\)
	\(\mathrm{C}_8^5\cdot2^3\cdot3^5\)