Từ nhà thầy Thơ đến nhà Lăm có thể đi bằng đường bộ hoặc đường thủy, trong đó đường bộ có $4$ tuyến, đường thủy có $3$ tuyến. Thầy Thơ muốn đến nhà Lăm để gặp phụ huynh thì có bao nhiêu cách chọn?
| $7$ | |
| $12$ | |
| $24$ | |
| $1$ |
Thầy Thơ vào shop thời trang Mơ Huyền để chọn mua một chiếc áo somi hoặc một chiếc caravat chuẩn bị cho ngày 20-11. Trong shop có $7$ mẫu áo và $5$ mẫu caravat phù hợp. Hỏi thầy Thơ có bao nhiêu sự lựa chọn?
| $12$ | |
| $35$ | |
| $21$ | |
| $1$ |
Thầy Thơ vào shop thời trang Mơ Huyền để chọn mua một chiếc áo somi và một chiếc caravat chuẩn bị cho ngày 20-11. Trong shop có $7$ mẫu áo và $5$ mẫu caravat phù hợp. Hỏi thầy Thơ có bao nhiêu sự lựa chọn?
| $12$ | |
| $35$ | |
| $21$ | |
| $1$ |
Bạn Tín có $4$ chiếc tem khác nhau và $3$ bì thư khác nhau. Có bao nhiêu cách chọn ra một chiếc tem và một bì thư để dán vào nhau?
| $7$ | |
| $12$ | |
| $24$ | |
| $1$ |
Bạn Tín có $4$ chiếc smartphone khác nhau và $3$ chiếc xe khác nhau. Tín muốn chụp hình một món trong số đó để khoe trên Facebook, hỏi Tín có bao nhiêu cách chọn?
| $7$ | |
| $12$ | |
| $24$ | |
| $1$ |
Từ một nhóm học sinh gồm $5$ nam và $3$ nữ, có bao nhiêu cách chọn ra một đôi song ca nam nữ?
| $8$ | |
| $15$ | |
| $10$ | |
| $60$ |
Từ một nhóm học sinh gồm $5$ nam và $3$ nữ, có bao nhiêu cách chọn ra một học sinh?
| $8$ | |
| $15$ | |
| $10$ | |
| $60$ |
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, hình chiếu của $S$ trên $(ABCD)$ trùng với trung điểm của cạnh $AB$, cạnh bên $SD=\dfrac{3a}{2}$. Tính thể tích $V$ của khối chóp $S.ABCD$ theo $a$.
Giải phương trình $\log_2x+\log_2(x-6)=\log_27$.
Tìm các điểm cực trị hàm số $f(x)=x^3-3x+1$.
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng $3$ lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài.
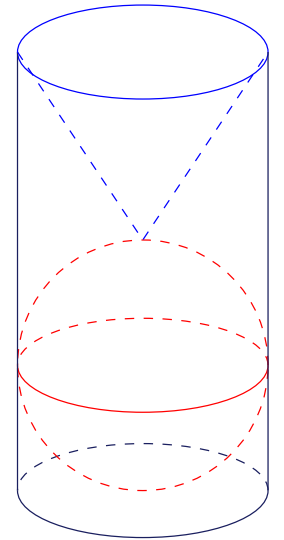
Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
| $\dfrac{1}{2}$ | |
| $\dfrac{2}{3}$ | |
| $\dfrac{4}{9}$ | |
| $\dfrac{5}{9}$ |
Thiết diện qua trục của một hình nón tròn xoay là tam giác đều có diện tích bằng $a^2\sqrt{3}$. Tính thể tích $V$ của khối nón đã cho.
| $V=\dfrac{\pi a^3\sqrt{3}}{3}$ | |
| $V=\dfrac{\pi a^3\sqrt{3}}{2}$ | |
| $V=\dfrac{\pi a^3\sqrt{3}}{6}$ | |
| $V=\dfrac{\pi a^3\sqrt{6}}{6}$ |
Hình hộp chữ nhật không nắp có thể tích $3200$cm$^3$, tỉ số giữa chiều cao và chiều rộng bằng $2$. Khi tổng diện tích các mặt của hình hộp nhỏ nhất, tính diện tích mặt đáy của hình hộp.
| $1200$cm$^2$ | |
| $120$cm$^2$ | |
| $160$cm$^2$ | |
| $1600$cm$^2$ |
Cho lăng trụ $ABC.A'B'C'$ có thể tích $V$. Tính thể tích $V_1$ của khối đa diện $BCA'B'C'$ theo $V$.
| $V_1=\dfrac{2}{3}V$ | |
| $V_1=\dfrac{1}{3}V$ | |
| $V_1=\dfrac{1}{2}V$ | |
| $V_1=\dfrac{1}{4}V$ |
Số mặt phẳng đối xứng của hình chóp tứ giác đều $S.ABCD$ là
| $2$ | |
| $4$ | |
| $7$ | |
| $6$ |
Trong các hình đa diện đều sau, hình nào có số đỉnh nhỏ hơn số mặt?
| Hình tứ diện đều | |
| Hình $20$ mặt đều | |
| Hình lập phương | |
| Hình $12$ mặt đều |
Một hình chóp $100$ cạnh có bao nhiêu mặt?
| $53$ | |
| $51$ | |
| $50$ | |
| $52$ |
Hình lăng trụ tam giác có bao nhiêu mặt?
| $6$ | |
| $3$ | |
| $9$ | |
| $5$ |
Gọi $x_1,\,x_2$ là hai nghiệm của phương trình $5^{x-1}=2^{x^2-1}$. Tính $P=\left(x_1+1\right)\left(x_2+1\right)$.
| $0$ | |
| $2\log_25+2$ | |
| $2\log_25-1$ | |
| $\log_225$ |
Nghiệm thực của phương trình $9^x-4\cdot3^x-45=0$ là
| $x=9$ | |
| $x=-5$ hoặc $x=9$ | |
| $x=2$ hoặc $x=\log_35$ | |
| $x=2$ |
