Cho khối chóp $S.ABC$ có đáy là tam giác vuông cân tại $A$, $AB=2$, $SA$ vuông góc với đáy và $SA=3$ (tham khảo hình bên).
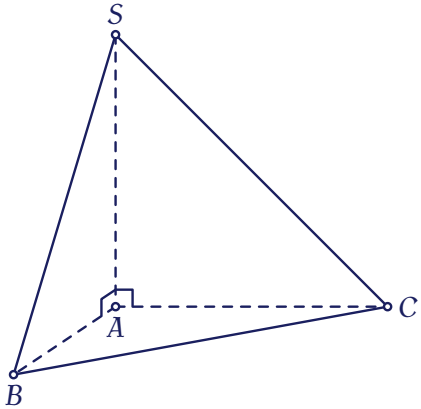
Thể tích khối chóp đã cho bằng
| $12$ | |
| $2$ | |
| $6$ | |
| $4$ |
Cho khối lập phương có cạnh bằng $2$. Thể tích của khối lập phương đã cho bằng
| $6$ | |
| $8$ | |
| $\dfrac{8}{3}$ | |
| $4$ |
Cho số phức $z=2+9i$, phần thực của số phức $z^2$ bằng
| $-77$ | |
| $4$ | |
| $36$ | |
| $85$ |
Trong không gian $Oxyz$, góc giữa hai mặt phẳng $(Oxy)$ và $(Oyz)$ bằng
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ | |
| $90^{\circ}$ |
Trong không gian $Oxyz$, cho mặt cầu $(S)\colon x^2+y^2+z^2-2x-4y-6z+1=0$. Tâm của $(S)$ có tọa độ là
| $(-1;-2;-3)$ | |
| $(2;4;6)$ | |
| $(-2;-4;-6)$ | |
| $(1;2;3)$ |
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
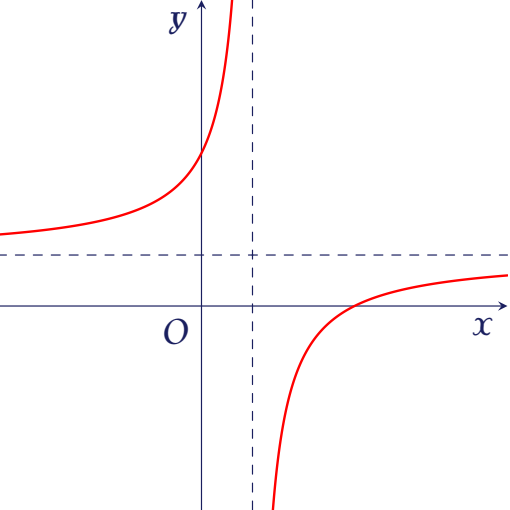
| $y=x^4-3x^2+2$ | |
| $y=\dfrac{x-3}{x-1}$ | |
| $y=x^2-4x+1$ | |
| $y=x^3-3x-5$ |
Nếu $\displaystyle\displaystyle\int_{-1}^4f(x)\mathrm{\,d}x=2$ và $\displaystyle\displaystyle\int_{-1}^4g(x)\mathrm{\,d}x=3$ thì $\displaystyle\displaystyle\int_{-1}^4\big[f(x)+g(x)\big]\mathrm{\,d}x$ bằng
| $5$ | |
| $6$ | |
| $1$ | |
| $-1$ |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình bên.
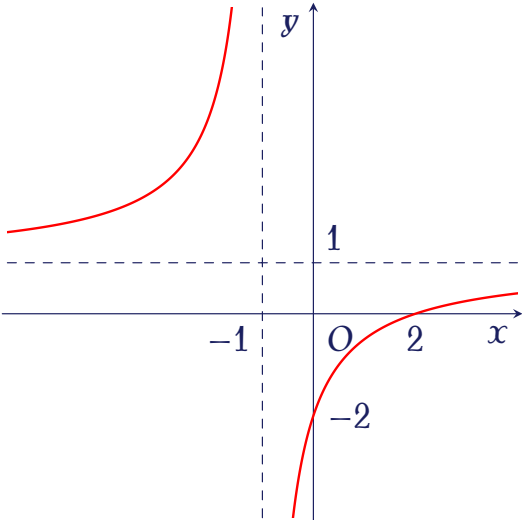
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
| $(0;-2)$ | |
| $(2;0)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
Trong không gian $Oxyz$, mặt phẳng $(P)\colon x+y+z+1=0$ có một vectơ pháp tuyến là
| $\overrightarrow{n_1}=(-1;1;1)$ | |
| $\overrightarrow{n_4}=(1;1;-1)$ | |
| $\overrightarrow{n_3}=(1;1;1)$ | |
| $\overrightarrow{n_2}=(1;-1;1)$ |
Cho cấp số nhân $\big(u_n\big)$ với $u_1=2$ và công bội $q=\dfrac{1}{2}$. Giá trị của $u_3$ bằng
| $3$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{1}{4}$ | |
| $\dfrac{7}{2}$ |
Tập nghiệm của bất phương trình $2^{x+1}< 4$ là
| $(-\infty;1]$ | |
| $(1;+\infty)$ | |
| $[1;+\infty)$ | |
| $(-\infty;1)$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=x^{\pi}$ là
| $y'=\pi x^{\pi-1}$ | |
| $y'=x^{\pi-1}$ | |
| $y'=\dfrac{1}{\pi}x^{\pi-1}$ | |
| $y'=\pi x^{\pi}$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=\log_3x$ là
| $y'=\dfrac{1}{x}$ | |
| $y'=\dfrac{1}{x\ln3}$ | |
| $y'=\dfrac{\ln3}{x}$ | |
| $y'=-\dfrac{1}{x\ln3}$ |
Trên mặt phẳng tọa độ, điểm biểu diễn số phức $z=7-6i$ có tọa độ là
| $(-6;7)$ | |
| $(6;7)$ | |
| $(7;6)$ | |
| $(7;-6)$ |
Một mảnh vườn hình elip có độ dài trục lớn $8$m và độ dài trục nhỏ $6$m. Người ta cần trồng rau trên dải đất rộng $4$m như hình vẽ.
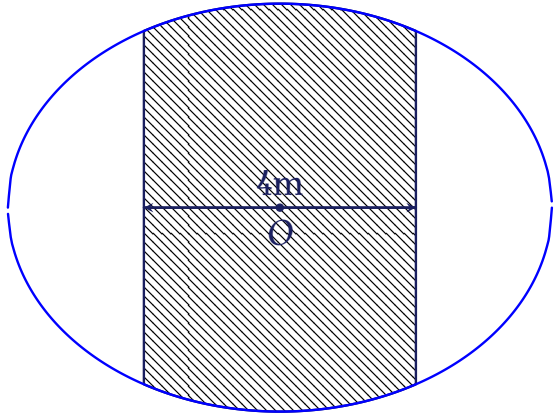
Hỏi cần bao nhiêu tiền để trồng rau trên dải đất đó, biết rằng kinh phí trồng rau là $70000$ đồng/m$^2$?
| $1.607.107$ đồng | |
| $803.553$ đồng | |
| $267.851$ đồng | |
| $2.638.938$ đồng |
Tìm $m$ để phương trình $(m-2)x^2+3mx+m^2-4m+3=0$ có hai nghiệm trái dấu.
Giải bất phương trình $\dfrac{1}{x-1}+\dfrac{2}{x-2}>0$.
Tiệm cận ngang của đồ thị hàm số $y=3^x$ và tiệm cận đứng của đồ thị hàm số $y=\log_2x$ lần lượt có phương trình là
| $y=3$ và $x=0$ | |
| $x=0$ và $y=0$ | |
| $y=0$ và $x=2$ | |
| $y=0$ và $x=0$ |
Trong không gian với hệ tọa độ $Oxyz$, cho điểm $I(1;-1;2)$ và mặt phẳng $(P)$ có phương trình $x+3y-z+2=0$.
- Viết phương trình mặt cầu $(S)$ tâm $I$, tiếp xúc với mặt phẳng $(P)$.
- Tìm tọa độ tiếp điểm của mặt cầu $(S)$ và mặt phẳng $(P)$.
Tìm hai số thực $x,\,y$ thỏa mãn $(2x-y)i+y(1-2i)^2=3+7i$.
