Trong không gian \(Oxyz\), cho ba điểm \(A(1;-2;3)\), \(B(4;2;3)\), \(C(3;4;3)\). Gọi \(\left(S_1\right),\,\left(S_2\right),\,\left(S_3\right)\) là các mặt cầu có tâm \(A,\,B,\,C\) và bán kính lần lượt là \(3,\,2,\,3\). Hỏi có bao nhiêu mặt phẳng qua điểm \(I\left(\dfrac{14}{5};\dfrac{2}{5};3\right)\) và tiếp xúc với cả ba mặt cầu \(\left(S_1\right),\,\left(S_2\right),\,\left(S_3\right)\)?
| \(2\) | |
| \(7\) | |
| \(0\) | |
| \(1\) |
Trong không gian \(Oxyz\), cho mặt phẳng \((P)\colon2x+3y+4z-5=0\) và điểm \(A(1;-3;1)\). Tính khoảng cách \(\mathrm{d}\) từ điểm \(A\) đến mặt phẳng \((P)\).
| \(\mathrm{d}=\dfrac{8}{9}\) | |
| \(\mathrm{d}=\dfrac{8}{29}\) | |
| \(\mathrm{d}=\dfrac{8}{\sqrt{29}}\) | |
| \(\mathrm{d}=\dfrac{3}{\sqrt{29}}\) |
Trong không gian \(Oxyz\), cho hai mặt phẳng \((P)\colon x+my+(m-1)z+1=0\) và \((Q)\colon x+y+2z=0\). Tập hợp tất cả các giá trị \(m\) để hai mặt phẳng này không song song là
| \((0;+\infty)\) | |
| \(\mathbb{R}\setminus\{-1;1;2\}\) | |
| \((-\infty;3)\) | |
| \(\mathbb{R}\) |
Trong không gian \(Oxyz\) cho điểm \(H(1;2;3)\). Viết phương trình mặt phẳng \((P)\) đi qua điểm \(H\) và cắt các trục tọa độ tại ba điểm phân biệt \(A,\,B,\,C\) sao cho \(H\) là trực tâm của tam giác \(ABC\).
| \((P)\colon x+\dfrac{y}{2}+\dfrac{z}{3}=1\) | |
| \((P)\colon x+2y+3z-14=0\) | |
| \((P)\colon x+y+z-6=0\) | |
| \((P)\colon\dfrac{x}{3}+\dfrac{y}{6}+\dfrac{z}{9}=1\) |
Trong không gian \(Oxyz\), cho mặt cầu \((S)\) có tâm \(I(3;2;-1)\) và đi qua điểm \(A(2;1;2)\). Mặt phẳng nào dưới đây tiếp xúc với \((S)\) tại \(A\)?
| \(x+y-3z-8=0\) | |
| \(x+y-3z+3=0\) | |
| \(x+y+3z-9=0\) | |
| \(x-y-3z+3=0\) |
Trong không gian \(Oxyz\), phương trình mặt phẳng \((Oxz)\) là
| \(x=0\) | |
| \(x+z=0\) | |
| \(z=0\) | |
| \(y=0\) |
Trong không gian \(Oxyz\), gọi \((\alpha)\) là mặt phẳng cắt ba trục tọa độ tại ba điểm \(A(4;0;0)\), \(B(0;-2;0)\) và \(C(0;0;6)\). Phương trình của \((\alpha)\) là
| \(\dfrac{x}{4}+\dfrac{y}{-2}+\dfrac{z}{6}=0\) | |
| \(\dfrac{x}{2}+\dfrac{y}{-1}+\dfrac{z}{3}=1\) | |
| \(\dfrac{x}{4}+\dfrac{y}{-2}+\dfrac{z}{6}=1\) | |
| \(3x-6y+2z-1=0\) |
Trong không gian \(Oxyz\), cho hai điểm \(A(1;-2;3)\) và \(B(5;4;7)\). Phương trình mặt cầu nhận \(AB\) làm đường kính là
| \((x-6)^2+(y-2)^2+(z-10)^2=17\) | |
| \((x-1)^2+(y+2)^2+(z-3)^2=17\) | |
| \((x-3)^2+(y-1)^2+(z-5)^2=17\) | |
| \((x-5)^2+(y-4)^2+(z-7)^2=17\) |
Trong không gian \(Oxyz\), cho \(A(1;-1;0)\), \(B(0;2;0)\) và \(C(2;1;3)\). Tọa độ điểm \(M\) thỏa mãn \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\) là
| \(M(3;2;-3)\) | |
| \(M(3;-2;3)\) | |
| \(M(3;-2;-3)\) | |
| \(M(3;2;3)\) |
Trong không gian \(Oxyz\), điểm nào dưới đây thuộc trục \(Oy\)?
| \(N(2;0;0)\) | |
| \(Q(0;3;2)\) | |
| \(P(2;0;3)\) | |
| \(M(0;-3;0)\) |
Cho số phức \(z=3-5i\). Gọi \(a,\,b\) lần lượt là phần thực và phần ảo của \(z\). Tính \(S=a+b\).
| \(S=-8\) | |
| \(S=8\) | |
| \(S=2\) | |
| \(S=-2\) |
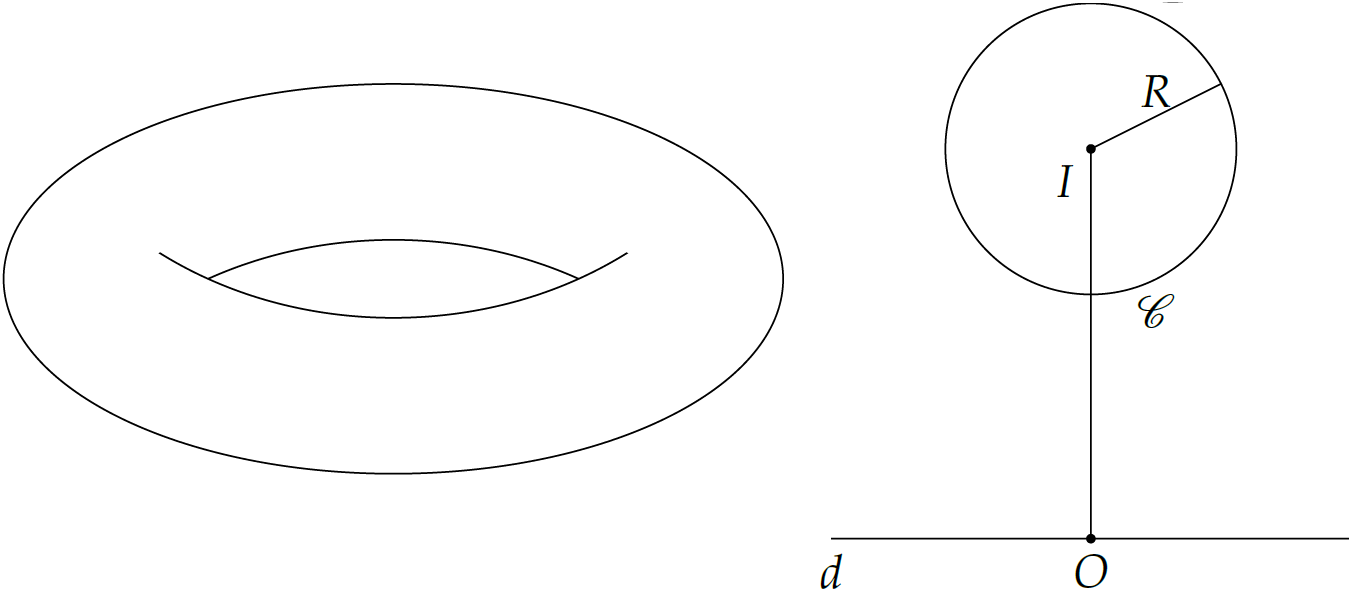
Người ta làm một chiếc phao bơi như hình vẽ (với bề mặt có được bằng cách quay đường tròn \(\mathscr{C}\) quanh trục \(d\)). Biết rằng \(OI=30\)cm, \(R=5\)cm. Tính thể tích \(V\) của chiếc phao.
| \(V=1500\pi^2\text{cm}^3\) | |
| \(V=9000\pi^2\text{cm}^3\) | |
| \(V=1500\pi\text{cm}^3\) | |
| \(V=9000\pi\text{cm}^3\) |
Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol \((P)\colon y=x^2\) và đường thẳng \(d\colon y=x\) xoay quanh trục \(Ox\) bằng
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x-\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x+\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)^2\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)\mathrm{\,d}x\) |
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị các hàm số \(y=x^2-2x\), \(y=0\), \(x=-1\), \(x=2\) quanh trục \(Ox\) bằng
| \(\dfrac{16\pi}{5}\) | |
| \(\dfrac{17\pi}{5}\) | |
| \(\dfrac{18\pi}{5}\) | |
| \(\dfrac{5\pi}{18}\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị các hàm số \(y=|x|\) và \(y=x^2-2\).
| \(S=\dfrac{20}{3}\) | |
| \(S=\dfrac{11}{2}\) | |
| \(S=3\) | |
| \(S=\dfrac{13}{3}\) |
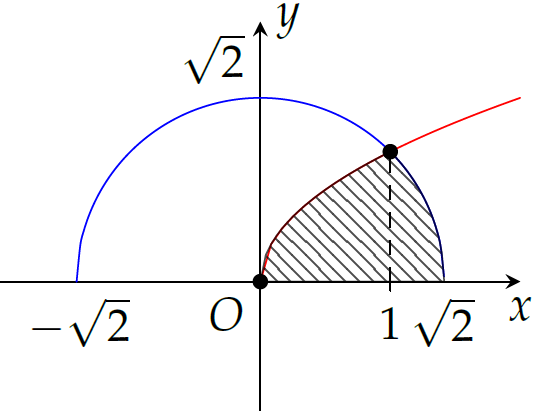
Cho \((H)\) là hình phẳng giới hạn bởi đường cong có phương trình \(y=\sqrt{x}\), nửa đường tròn có phương trình \(y=\sqrt{2-x^2}\) (với \(0\leq x\leq\sqrt{2}\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \((H)\) bằng
| \(\dfrac{3\pi+2}{12}\) | |
| \(\dfrac{4\pi+2}{12}\) | |
| \(\dfrac{3\pi+1}{12}\) | |
| \(\dfrac{4\pi+1}{6}\) |
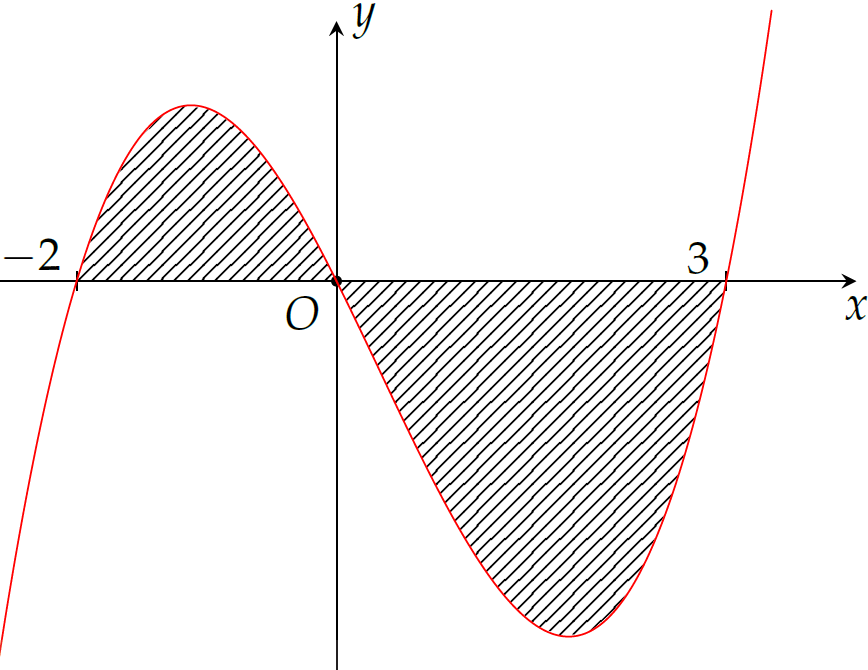
Cho đồ thị hàm số \(y=f(x)\) như hình vẽ và \(\displaystyle\int\limits_{-2}^{0}f(x)\mathrm{\,d}x=a\), \(\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=b\). Tính diện tích của phần được gạch chéo theo \(a\) và \(b\).
| \(\dfrac{a+b}{2}\) | |
| \(a-b\) | |
| \(b-a\) | |
| \(a+b\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\). Diện tích hình phẳng giới hạn bởi đường cong \(y=f(x)\), trục hoành, các đường thẳng \(x=a\), \(x=b\) là
| \(\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) |
Một ô tô đang đi với vận tốc lớn hơn \(72\)km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là \(72\)km/h, vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc \(v(t)=30-2t\) (m/s), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ \(72\)km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét?
| \(100\)m | |
| \(150\)m | |
| \(175\)m | |
| \(125\)m |
Giá trị nào của \(a\) để $$\displaystyle\int\limits_{0}^{a}\left(3x^2+2\right)\mathrm{\,d}x=a^3+2?$$
| \(1\) | |
| \(2\) | |
| \(0\) | |
| \(3\) |
