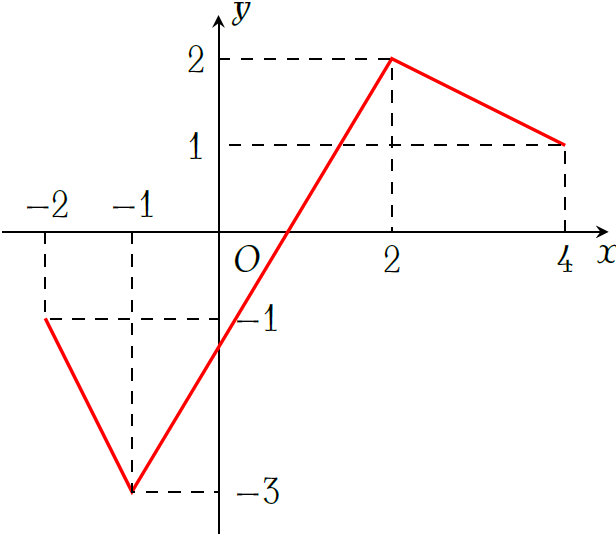
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ. Tìm \(\max\limits_{[-2;4]}\left|f(x)\right|\).

	\(\left|f(0)\right|\)
	\(2\)
	\(3\)
	\(1\)

Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x+\dfrac{1}{x}\) trên đoạn \(\left[\dfrac{1}{2};3\right]\). Khi đó \(M+m\) bằng

	\(\dfrac{9}{2}\)
	\(\dfrac{35}{6}\)
	\(\dfrac{7}{2}\)
	\(\dfrac{16}{3}\)

Cho hàm số \(y=\dfrac{3x-1}{x+2}\). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn \([0;2]\). Khi đó \(4M-2m\) bằng

	\(10\)
	\(6\)
	\(5\)
	\(4\)

Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-3;2]\) và có bảng biến thiên như sau: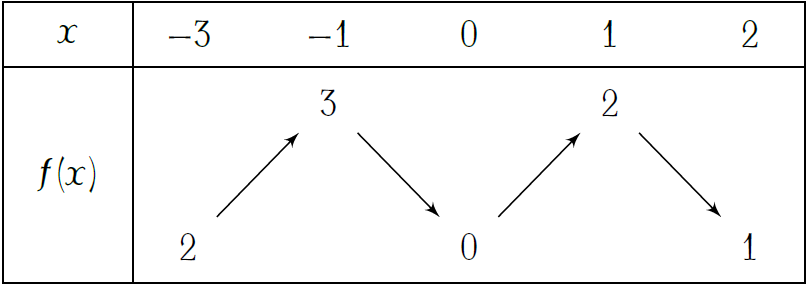

Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(f(x)\) trên đoạn \([-1;2]\). Tính \(M+m\).

	\(3\)
	\(2\)
	\(1\)
	\(4\)

Gọi \(M,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y=x^3-3x^2+1\) trên đoạn \([1;2]\). Khi đó tổng \(M+N\) bằng

	\(2\)
	\(-2\)
	\(0\)
	\(-4\)

Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x\sqrt{1-x^2}\). Khi đó \(M-m\) bằng

	\(1\)
	\(2\)
	\(4\)
	\(3\)

Giá trị lớn nhất của hàm số \(y=\sqrt{1-x^2}\) bằng

	\(1\)
	\(0\)
	\(-1\)
	\(2\)

Tìm tập giá trị \(T\) của hàm số $$y=\sqrt{x-1}+\sqrt{9-x}$$

	\(T=[1;9]\)
	\(T=\left[0;2\sqrt{2}\right]\)
	\(T=(1;9)\)
	\(T=\left[2\sqrt{2};4\right]\)

Giá trị nhỏ nhất \(m\) của hàm số \(y=x^3-3x+5\) trên đoạn \([2;4]\) là

	\(0\)
	\(5\)
	\(7\)
	\(3\)

Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+3}{2x-3}\) trên đoạn \([2;5]\).

	\(\dfrac{7}{8}\)
	\(\dfrac{8}{7}\)
	\(5\)
	\(\dfrac{2}{7}\)

Tìm giá trị nhỏ nhất của hàm số \(y=\dfrac{x+1}{x-1}\) trên đoạn \([2;3]\).

	\(-3\)
	\(3\)
	\(2\)
	\(4\)

Tìm giá trị lớn nhất của hàm số \(y=\dfrac{3x-1}{x-3}\) trên đoạn \([0;2]\).

	\(-\dfrac{1}{3}\)
	\(-5\)
	\(5\)
	\(\dfrac{1}{3}\)

Hàm số nào sau đây không có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \([-2;2]\).

	\(y=\dfrac{x-1}{x+1}\)
	\(y=x^2\)
	\(y=1-x\)
	\(y=x^3+2\)

Tìm giá trị lớn nhất của hàm số $$y=3+\sqrt{x^2-2x+8}$$trên đoạn \([-2;2]\).

	\(7\)
	\(9\)
	\(3+2\sqrt{2}\)
	\(3+\sqrt{7}\)

Tìm giá trị nhỏ nhất của hàm số \(y=x+1+\dfrac{4}{x}\) trên đoạn \([1;3]\).

	\(4\)
	\(\dfrac{16}{3}\)
	\(5\)
	\(6\)

Giải phương trình $$4\sin x\cdot\cos3x=1-2\sin2x$$ 

	\(\left[\begin{array}{l}x=\dfrac{\pi}{6}+k2\pi\\ x=\dfrac{5\pi}{6}+k2\pi\end{array}\right.\,\left(k\in\mathbb{Z}\right)\)
	\(\left[\begin{array}{l}x=\dfrac{\pi}{6}+k\pi\\ x=\dfrac{5\pi}{6}+k\pi\end{array}\right.\,\left(k\in\mathbb{Z}\right)\)
	\(\left[\begin{array}{l}x=\dfrac{\pi}{24}+\dfrac{k\pi}{2}\\ x=\dfrac{5\pi}{24}+\dfrac{k\pi}{2}\end{array}\right.\,\left(k\in\mathbb{Z}\right)\)
	\(\left[\begin{array}{l}x=\dfrac{\pi}{24}+k2\pi\\ x=\dfrac{5\pi}{24}+k2\pi\end{array}\right.\,\left(k\in\mathbb{Z}\right)\)

Phương trình \(\tan^2x-2\sqrt{3}\tan x+3=0\) có bao nhiêu nghiệm trên đoạn \(\left[-10\pi;10\pi\right]\)?

	\(9\)
	\(10\)
	\(19\)
	\(20\)

Tìm tham số \(m\) để phương trình $$m\sin x-\cos x=\sqrt{5}$$có nghiệm.

	\(\left[\begin{array}{l}m\le-2\\ m\ge2\end{array}\right.\)
	\(-2\le m\le2\)
	\(\left[\begin{array}{l}m\le-\sqrt{6}\\ m\ge\sqrt{6}\end{array}\right.\)
	\(-\sqrt{6}\le m\le\sqrt{6}\)

Giải phương trình \(\sqrt{3}\sin x+\cos x=2\).

	\(x=\dfrac{\pi}{2}+k2\pi\,\left(k\in\mathbb{Z}\right)\)
	\(x=\dfrac{\pi}{3}+k2\pi\,\left(k\in\mathbb{Z}\right)\)
	\(x=\dfrac{\pi}{6}+k2\pi\,\left(k\in\mathbb{Z}\right)\)
	\(x=\dfrac{2\pi}{3}+k2\pi\,\left(k\in\mathbb{Z}\right)\)

Giải phương trình \(\cos^2x+\cos x=0\).

	\(\left[\begin{array}{l}x=\dfrac{\pi}{2}+k\pi\\ x=\pi+k2\pi\end{array}\right.\,\left(k\in\mathbb{Z}\right)\)
	\(\left[\begin{array}{l}x=\dfrac{\pi}{2}+k2\pi\\ x=k\pi\end{array}\right.\,\left(k\in\mathbb{Z}\right)\)
	\(\left[\begin{array}{l}x=\pm \dfrac{\pi}{2}+k2\pi\\ x=k\pi\end{array}\right.\,\left(k\in\mathbb{Z}\right)\)
	\(x=\dfrac{k\pi}{2}\,\left(k\in\mathbb{Z}\right)\)