Đồ thị của hàm số nào dưới đây có đường tiệm cận ngang?

	\(y=\dfrac{3x^2-1}{x+1}\)
	\(y=x^4-x^2-2\)
	\(y=\dfrac{2-x}{x}\)
	\(y=x^3-x^2+x-3\)

Đường thẳng \(y=2\) là tiệm cận ngang của đồ thị hàm số nào dưới đây?

	\(y=\dfrac{2x-1}{1-x}\)
	\(y=\dfrac{4x-1}{2x+5}\)
	\(y=\dfrac{x+1}{2x+1}\)
	\(y=\dfrac{2x-4}{2x+3}\)

Đồ thị hàm số \(f(x)=x^3+2x^2+3x+2021\) có bao nhiêu đường tiệm cận ngang?

	\(0\)
	\(1\)
	\(2\)
	\(3\)

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{1-4x}{2x-1}\)?

	\(y=2\)
	\(y=\dfrac{1}{2}\)
	\(y=4\)
	\(y=-2\)

Tìm tiệm cận ngang của đồ thị hàm số \(f(x)=1+\dfrac{2x+2}{x-1}\).

	\(x=1\)
	\(y=1\)
	\(y=2\)
	\(y=3\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2-2x}{x+1}\) là

	\(y=-2\)
	\(x=-1\)
	\(x=-2\)
	\(y=2\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{x-3}{x-1}\) là

	\(y=5\)
	\(y=0\)
	\(x=1\)
	\(y=1\)

Đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2x-3}{x+4}\) là

	\(x=-4\)
	\(y=2\)
	\(x=4\)
	\(y=-\dfrac{3}{4}\)

Trong không gian \(Oxyz\), cho ba điểm \(A\left(1;0;1\right)\), \(B\left(1;1;0\right)\) và \(C\left(3;4;-1\right)\). Đường thẳng đi qua \(A\) và song song với \(BC\) có phương trình là

	\(\dfrac{x-1}{4}=\dfrac{y}{5}=\dfrac{z-1}{-1}\)
	\(\dfrac{x+1}{2}=\dfrac{y}{3}=\dfrac{z+1}{-1}\)
	\(\dfrac{x-1}{2}=\dfrac{y}{3}=\dfrac{z-1}{-1}\)
	\(\dfrac{x+1}{4}=\dfrac{y}{5}=\dfrac{z+1}{-1}\)

Trong không gian \(Oxyz\), cho đường thẳng \(d\colon\dfrac{x-3}{2}=\dfrac{y-4}{-5}=\dfrac{z+1}{3}\). Vectơ nào dưới đây là một vectơ chỉ phương của \(d\)?

	\(\overrightarrow{u_2}=\left(2;4;-1\right)\)
	\(\overrightarrow{u_1}=\left(2;-5;3\right)\)
	\(\overrightarrow{u_3}=\left(2;5;3\right)\)
	\(\overrightarrow{u_4}=\left(3;4;1\right)\)

Trong không gian \(Oxyz\), cho điểm \(M\left(2;-2;3\right)\) và đường thẳng \(d\colon\dfrac{x-1}{3}=\dfrac{y+2}{2}=\dfrac{z-3}{-1}\). Mặt phẳng đi qua \(M\) và vuông góc với \(d\) có phương trình là

	\(3x+2y-z+1=0\)
	\(2x-2y+3z-17=0\)
	\(3x+2y-z-1=0\)
	\(2x-2y+3z+17=0\)

Trong không gian \(Oxyz\), cho ba điểm \(A\left(3;0;0\right)\), \(B\left(0;1;0\right)\) và \(C\left(0;0;-2\right)\). Mặt phẳng \(\left(ABC\right)\) có phương trình là

	\(\dfrac{x}{3}+\dfrac{y}{-1}+\dfrac{z}{2}=1\)
	\(\dfrac{x}{3}+\dfrac{y}{1}+\dfrac{z}{-2}=1\)
	\(\dfrac{x}{3}+\dfrac{y}{1}+\dfrac{z}{2}=1\)
	\(\dfrac{x}{-3}+\dfrac{y}{1}+\dfrac{z}{2}=1\)

Trong không gian \(Oxyz\), cho mặt cầu \(\left(S\right)\colon x^2+y^2+\left(z+2\right)^2=9\). Bán kính của \(\left(S\right)\) bằng

	\(6\)
	\(18\)
	\(9\)
	\(3\)

Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(A\left(3;2;1\right)\) trên trục \(Ox\) có tọa độ là

	\(\left(0;2;1\right)\)
	\(\left(3;0;0\right)\)
	\(\left(0;0;1\right)\)
	\(\left(0;2;0\right)\)

Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(CC'\) (tham khảo hình vẽ).

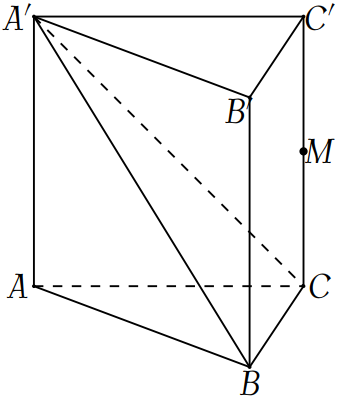
Khoảng cách từ \(M\) đến mặt phẳng \(\left(A'BC\right)\) bằng

	\(\dfrac{\sqrt{21}a}{14}\)
	\(\dfrac{\sqrt{2}a}{2}\)
	\(\dfrac{\sqrt{21}a}{7}\)
	\(\dfrac{\sqrt{2}a}{4}\)

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB=a\), \(BC=2a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA=\sqrt{15}a\) (tham khảo hình vẽ).

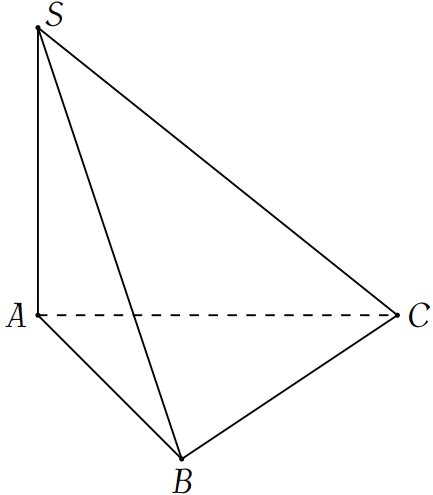
Góc giữa đường thẳng \(SC\) và mặt phẳng đáy bằng

	\(45^\circ\)
	\(30^\circ\)
	\(60^\circ\)
	\(90^\circ\)

Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(4a\), \(SA\) vuông góc với mặt phẳng đáy, góc giữa mặt phẳng \(\left(SBC\right)\) và mặt phẳng đáy bằng \(60^\circ\). Diện tích của mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng

	\(\dfrac{172\pi a^2}{3}\)
	\(\dfrac{76\pi a^2}{3}\)
	\(84\pi a^2\)
	\(\dfrac{172\pi a^2}{9}\)

Cho khối cầu có bán kính \(r=4\). Thể tích của khối cầu đã cho bằng

	\(\dfrac{256\pi}{3}\)
	\(64\pi\)
	\(\dfrac{64\pi}{3}\)
	\(256\pi\)

Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên bằng \(2a\) và \(O\) là tâm của đáy. Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là các điểm đối xứng với \(O\) qua trọng tâm của các tam giác \(SAB\), \(SBC\), \(SCD\), \(SDA\) và \(S'\) là điểm đối xứng với \(S\) qua \(O\). Thể tích của khối chóp \(S'.MNPQ\) bằng

	\(\dfrac{20\sqrt{14}{a^3}}{81}\)
	\(\dfrac{40\sqrt{14}{a^3}}{81}\)
	\(\dfrac{10\sqrt{14}{a^3}}{81}\)
	\(\dfrac{2\sqrt{14}{a^3}}{9}\)

Cho hình nón có bán kính đáy bằng \(2\) và góc ở đỉnh bằng \(60^\circ\). Diện tích xung quanh của hình nón đã cho bằng

	\(8\pi\)
	\(\dfrac{16\sqrt{3}\pi}{3}\)
	\(\dfrac{8\sqrt{3}\pi}{3}\)
	\(16\pi\)