Hàm số $y=\sqrt{x+2}-\sqrt{3-x}$ có tập xác định là
| $\left[-2;3\right]$ | |
| $\left[-2;+\infty\right)$ | |
| $\left[3;+\infty\right)$ | |
| $\left(-\infty;3\right]$ |
Tìm tập xác định $\mathscr{D}$ của hàm số $y=\dfrac{3x-1}{2x-2}$.
| $\mathscr{D}=\Bbb{R}$ | |
| $\mathscr{D}=\Bbb{R}\setminus\left\{2\right\}$ | |
| $\mathscr{D}=\left[1;+\infty\right)$ | |
| $\mathscr{D}=\Bbb{R}\setminus\left\{1\right\}$ |
Cho hàm số $f\left(x\right)=\begin{cases}\dfrac{2}{x-1} &\text{nếu }x\in\left(-\infty;0\right)\\ \sqrt{x+1} &\text{nếu }x\in\left[0;2\right]\\ x^2-1 &\text{nếu }x\in\left(2;5\right]\end{cases}$. Tính $f\left(4\right)$.
| $f\left(4\right)=\dfrac{2}{3}$ | |
| $f\left(4\right)=15$ | |
| $f\left(4\right)=\sqrt{5}$ | |
| Không tồn tại |
Cho hàm số $f\left(x\right)=\left|-5x\right|$. Chọn mệnh đề sai?
| $f\left(-1\right)=5$ | |
| $f\left(2\right)=10$ | |
| $f\left(-2\right)=10$ | |
| $f\left(\dfrac{1}{5}\right)=-1$ |
Điểm nào sau đây thuộc đồ thị hàm số $y=\dfrac{1}{x-1}$?
| $M\left(1;1\right)$ | |
| $N\left(2;1\right)$ | |
| $P\left(2;0\right)$ | |
| $Q\left(0;-2\right)$ |
Tìm tọa độ giao điểm của parabol \(y=-x^2+2x+1\) với đường thẳng \(y=2x-3\).
| \((2;1)\) | |
| \((2;-2)\) và \((1;-7)\) | |
| \((2;1)\) và \((-2;-7)\) | |
| \((-2;-7)\) |
Đồ thị của hàm số \(y=x^2+4x+1\) là đường cong nào dưới đây?
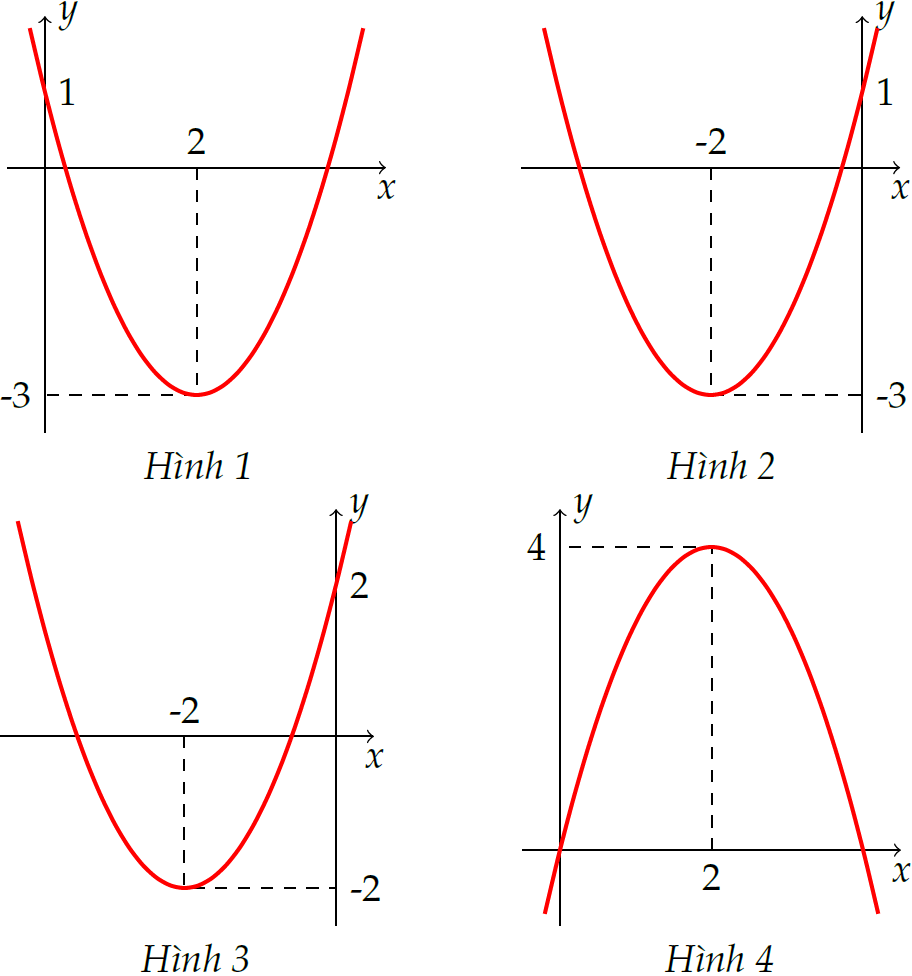
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Hình vẽ sau đây là đồ thị của hàm số nào?
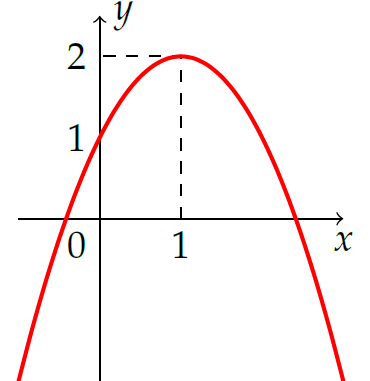
| \(y=-x^2+2x\) | |
| \(y=x^2-2x+1\) | |
| \(y=-x^2-2x+1\) | |
| \(y=-x^2+2x+1\) |
Hàm số \(y=x^2+4x+1\) đồng biến trên khoảng
| \((-\infty;-2)\) | |
| \((-2;+\infty)\) | |
| \((2;+\infty)\) | |
| \((-\infty;+\infty)\) |
Parabol \(y=x^2-x+3\) có đỉnh là
| \(A\left(\dfrac{1}{2};\dfrac{11}{4}\right)\) | |
| \(x=\dfrac{1}{2}\) | |
| \(B\left(-\dfrac{1}{2};\dfrac{15}{4}\right)\) | |
| \(I(1;3)\) |
Hình vẽ sau đây là đồ thị của hàm số nào?
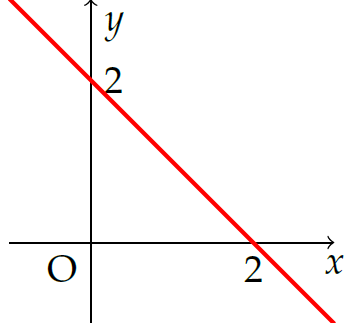
| \(y=2-x\) | |
| \(y=x-2\) | |
| \(y=2-2x\) | |
| \(y=1-2x\) |
Hình vẽ nào dưới đây là đồ thị của hàm số \(y=\dfrac{x}{2}-2\)?
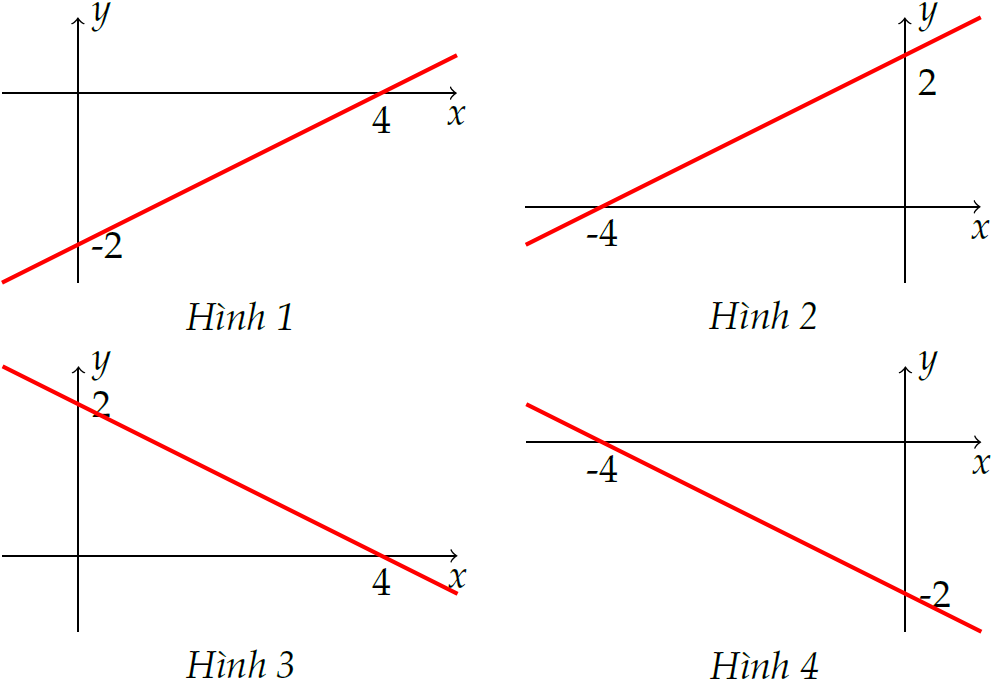
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Đường thẳng \(\Delta\) đi qua điểm \(M(6;13)\) và vuông góc với đường thẳng \(d\colon y=3x-2019\) có phương trình là
| \(y=3x-5\) | |
| \(y=\dfrac{x}{3}+11\) | |
| \(y=-\dfrac{x}{3}-2019\) | |
| \(y=-\dfrac{x}{3}+15\) |
Tìm điều kiện của tham số \(m\) để hàm số \(y=(m-3)x+2019\) luôn nghịch biến trên \(\Bbb{R}\).
| \(m>3\) | |
| \(m\leq3\) | |
| \(m<3\) | |
| \(m\neq3\) |
Hàm số nào dưới đây là hàm số chẵn?
| \(y=\sqrt{x-3}\) | |
| \(y=-x^4+3x^2-2019\) | |
| \(y=(x-3)^2\) | |
| \(y=2x^3-2019x\) |
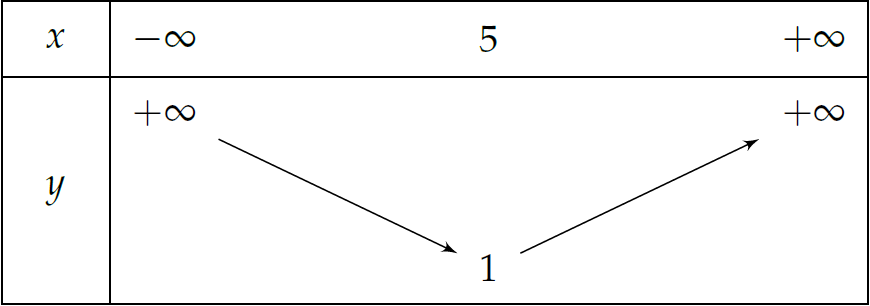
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Tìm khoảng đồng biến của hàm số.
| \((-\infty;5)\) | |
| \((-\infty;1)\) | |
| \((1;+\infty)\) | |
| \((5;+\infty)\) |
Tìm tập xác định của hàm số $$f(x)=\dfrac{x+7}{\sqrt{x-7}}$$
| \(\mathscr{D}=(7;+\infty)\) | |
| \(\mathscr{D}=[7;+\infty)\) | |
| \(\mathscr{D}=\Bbb{R}\setminus\{7\}\) | |
| \(\mathscr{D}=(-\infty;7)\) |
Tìm tập xác định của hàm số $$f(x)=\dfrac{x+7}{x-7}$$
| \(\mathscr{D}=\Bbb{R}\setminus\{-7\}\) | |
| \(\mathscr{D}=\Bbb{R}\setminus\{\pm7\}\) | |
| \(\mathscr{D}=\Bbb{R}\) | |
| \(\mathscr{D}=\Bbb{R}\setminus\{7\}\) |
Điểm nào dưới đây thuộc đồ thị của hàm số \(f(x)=\sqrt{x-3}\)?
| \(A(5;2)\) | |
| \(B(0;-3)\) | |
| \(C(2;-1)\) | |
| \(D(3;0)\) |
