Hàm số nào sau đây có đồ thị là parabol có đỉnh $I(-1;3)$?
| $y=2x^2-4x-3$ | |
| $y=2x^2-2x-1$ | |
| $y=2x^2+4x+5$ | |
| $y=2x^2+x+2$ |
Parabol $\left(\mathscr{P}\right)\colon y=3x^2-2x+1$ có đỉnh là
| $A\left(-\dfrac{1}{3};\dfrac{2}{3}\right)$ | |
| $B\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $C\left(\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $D\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ |
Trong các hàm số sau, hàm số nào có đồ thị nhận đường thẳng $x=1$ làm trục đối xứng?
| $y=-2x^2+4x+1$ | |
| $y=2x^2+4x-3$ | |
| $y=2x^2-2x-1$ | |
| $y=x^2-x+2$ |
Trục đối xứng của parabol $\left(\mathscr{P}\right)\colon y=2x^2+6x+3$ là
| $x=-\dfrac{3}{2}$ | |
| $y=-\dfrac{3}{2}$ | |
| $x=-3$ | |
| $y=-3$ |
Cho hàm số $y=ax^2+bx+c$ $(a\neq0)$ có đồ thị $\left(\mathscr{P}\right)$. Tọa độ đỉnh của $\left(\mathscr{P}\right)$ là
| $I\left(-\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$ | |
| $I\left(-\dfrac{b}{a};-\dfrac{\Delta}{4a}\right)$ | |
| $I\left(-\dfrac{b}{2a};-\dfrac{\Delta}{4a}\right)$ | |
| $I\left(\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$ |
Cho hàm số $y=f(x)$ có đồ thị như hình vẽ.
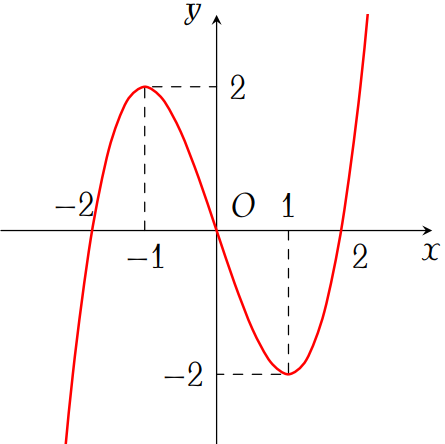
Khẳng định nào sau đây sai?
| $f(x)$ đồng biến trên khoảng $(1;2)$ | |
| $f(x)$ nghịch biến trên khoảng $(-1;0)$ | |
| $f(x)$ nghịch biến trên khoảng $(-1;1)$ | |
| $f(x)$ đồng biến trên khoảng $(0;2)$ |
Cho hàm số $y=f(x)$ xác định trên đoạn $[-3;3]$ và đồ thị của nó được biểu diễn bởi hình bên.

Khẳng định nào sau đây là đúng?
| Hàm số đồng biến trên khoảng $(-3;-1)$ và $(1;3)$ | |
| Hàm số đồng biến trên khoảng $(-3;-1)$ và $(1;4)$ | |
| Hàm số đồng biến trên khoảng $(-3;3)$ | |
| Hàm số nghịch biến trên khoảng $(-1;0)$ |
Điểm nào sau đây thuộc đồ thị hàm số $y=2|x-1|+3|x|-2$?
| $A(2;6)$ | |
| $B(1;-1)$ | |
| $C(-2;-10)$ | |
| Cả ba điểm $A,\,B,\,C$ |
Điểm nào sau đây không thuộc đồ thị hàm số $y=\dfrac{\sqrt{x^2-4x+4}}{x}$?
| $A(2;0)$ | |
| $B\left(3;\dfrac{1}{3}\right)$ | |
| $C(1;-1)$ | |
| $D(-1;-3)$ |
Điểm nào sau đây không thuộc đồ thị hàm số $y=x^4-2x^2-1$?
| $A(-1;2)$ | |
| $B(2;7)$ | |
| $C(0;-1)$ | |
| $D(1;-2)$ |
Cho hàm số $f(x)=\begin{cases}
\dfrac{2\sqrt{x+2}-3}{x-1} &\text{khi }x\geq2\\
x^2+1 &\text{khi }x<2
\end{cases}$. Khi đó, giá trị của $f(2)+f(-2)$ bằng
| $6$ | |
| $4$ | |
| $\dfrac{5}{3}$ | |
| $\dfrac{8}{3}$ |
Cho hàm số $f(x)=\begin{cases}
\dfrac{2}{x-1} &\text{khi }x\in(-\infty;0)\\
\sqrt{x+1} &\text{khi }x\in[0;2]\\
x^2-1 &\text{khi }x\in(2;5]
\end{cases}$. Tính $f(4)$ ta được kết quả
| $\dfrac{2}{3}$ | |
| $15$ | |
| $\sqrt{5}$ | |
| Kết quả khác |
Tính giá trị của hàm số $f(x)=x+1$ tại $x=2$.
| $0$ | |
| $3$ | |
| $2$ | |
| $-1$ |
Cho hàm số $f(x)=|-5x|$. Khẳng định nào sau đây là sai?
| $f(-1)=5$ | |
| $f(2)=10$ | |
| $f(-2)=10$ | |
| $f\left(\dfrac{1}{5}\right)=-1$ |
Xét tính chẵn lẻ của hai hàm số $f(x)=|x+2|-|x-2|$ và $g(x)=-|x|$.
| $f(x)$ chẵn, $g(x)$ chẵn | |
| $f(x)$ lẻ, $g(x)$ chẵn | |
| $f(x)$ lẻ, $g(x)$ lẻ | |
| $f(x)$ chẵn, $g(x)$ lẻ |
Cho hàm số $f(x)=|x+1|+|x-1|$. Mệnh đề nào sai?
| Hàm số $f(x)$ có tập xác định là $\mathbb{R}$ | |
| Đồ thị hàm số $f(x)$ nhận trục $Oy$ là trục đối xứng | |
| Hàm số $f(x)$ là hàm số chẵn | |
| Đồ thị hàm số $f(x)$ nhận gốc tọa độ là tâm đối xứng |
Trong các hàm số sau, hàm số nào không phải là hàm số lẻ?
| $y=-\dfrac{1}{x}$ | |
| $y=x^3+x$ | |
| $y=x^3-x$ | |
| $y=x^3+x^2$ |
Hàm số nào sau đây là hàm số lẻ?
| $y=2x$ | |
| $y=x^3+x^2$ | |
| $y=x^3+1$ | |
| $y=|x|+1$ |
Đồ thị hàm số nào sau đây nhận trục $Oy$ làm trục đối xứng?
| $y=x^3-|x|$ | |
| $y=x^2-|x|$ | |
| $y=x^2-x$ | |
| $y=x^3-x$ |
Hàm số $f(x)=x\left(x^4-3x^2-5\right)$ là hàm số
| vừa chẵn vừa lẻ | |
| lẻ | |
| chẵn | |
| không chẵn không lẻ |
