Cho tứ diện $ABCD$. Gọi $N,\,K$ lần lượt là trung điểm các cạnh $BC$ và $CD$, $M$ là điểm trên cạnh $AB$ sao cho $MB=2MA$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là
| Hình bình hành | |
| Hình thang | |
| Hình chữ nhật | |
| Hình thoi |
Cho tứ diện $ABCD$. Gọi $M,\,N,\,K$ lần lượt là trung điểm các cạnh $AB$, $BC$, $CD$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là
| Hình bình hành | |
| Hình thang | |
| Hình chữ nhật | |
| Hình thoi |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ có số đo
| $45^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a\sqrt{3}$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ có số đo
| $60^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $45^\circ$ |
Cho hình chóp $S.ABC$ có $SA\perp AB$ và $SA\perp BC$. Khẳng định nào sau đây không đúng?
| $AB\perp BC$ | |
| $SA\perp AC$ | |
| $SA\perp(ABC)$ | |
| $\big(SA,(ABC)\big)=90^\circ$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SCA}$ | |
| $\widehat{SCB}$ | |
| $\widehat{SAC}$ | |
| $\widehat{ASC}$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SBA}$ | |
| $\widehat{SBC}$ | |
| $\widehat{SAB}$ | |
| $\widehat{ASB}$ |
Cho hình lăng trụ có cạnh bên vuông góc với mặt đáy, khi đó các mặt bên của lăng trụ là hình gì?
| Hình chữ nhật | |
| Hình bình hành | |
| Hình thoi | |
| Hình vuông |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SC$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AC$ | |
| $BC$ | |
| $AB$ | |
| $SC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SB$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AB$ | |
| $BC$ | |
| $SB$ | |
| $AC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ có số đo là
| $90^\circ$ | |
| $0^\circ$ | |
| $180^\circ$ | |
| $90$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Khẳng định nào sau đây không đúng?
| $SB\perp BC$ | |
| $SA\perp AB$ | |
| $SA\perp AC$ | |
| $SA\perp BC$ |
Biết rằng $b,\,c$ là hai đường thẳng cắt nhau và cùng nằm trong mặt phẳng $(\alpha)$. Nếu đường thẳng $a$ vuông góc với cả $b$ và $c$ thì
| $a\perp(\alpha)$ | |
| $a\parallel(\alpha)$ | |
| $a\subset(\alpha)$ | |
| $a,\,b,\,c$ đồng quy |
Biết rằng đường thẳng $a$ vuông góc với mặt phẳng $(\alpha)$ và đường thẳng $b$ nằm trên mặt phẳng $(\alpha)$. Kết luận nào sau đây là đúng?
| $a\perp b$ | |
| $a\parallel b$ | |
| $a,\,b$ chéo nhau | |
| $a,\,b$ cắt nhau |
Trong không gian, cho tứ diện $ABCD$ có trọng tâm $S$. Gọi $G$ là trọng tâm tam giác $BCD$, $M$ và $N$ lần lượt là trung điểm của $AB$, $CD$. Mệnh đề nào sau đây là sai?
| $S$ là trung điểm đoạn $MN$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $S$ nằm trên đoạn $AG$ sao cho $SA=3SG$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ |
Trong không gian, cho tứ diện $ABCD$ có $M,\,N$ lần lượt là trung điểm của $AB,\,CD$. Chọn mệnh đề sai trong các mệnh đề sau:
| $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$ | |
| $\overrightarrow{NC}+\overrightarrow{NC}=\overrightarrow{0}$ | |
| $\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CM}$ | |
| $\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AM}$ |
Trong không gian, điểm $S$ là trọng tâm của tứ diện $ABCD$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}+\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=3\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{A0}$ |
Cho tứ diện $ABCD$ có $G$ là trọng tâm tam giác $BCD$. Mệnh đề nào sau đây không đúng?
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}$ | |
| $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ | |
| $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}-3\overrightarrow{AG}=\overrightarrow{0}$ |
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, $SA$ vuông góc với đáy và $SA=AB$ (tham khảo hình bên).
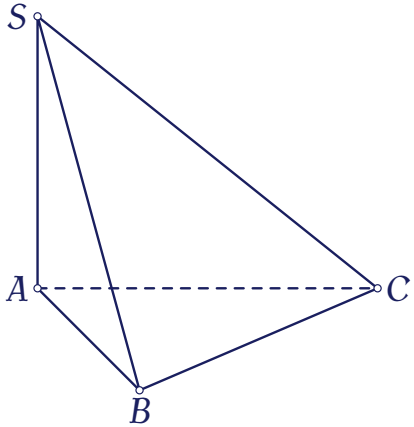
Góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ bằng
| $60^{\circ}$ | |
| $30^{\circ}$ | |
| $90^{\circ}$ | |
| $45^{\circ}$ |
Cho 5 khẳng định sau về hình lăng trụ. Hỏi có bao nhiêu khẳng định đúng?
- Hình lăng trụ có tất cả các mặt bên đều là hình bình hành;
- Hình lăng trụ có 2 đáy là những đa giác bằng nhau và nằm trên 2 mặt phẳng song song;
- Hình lăng trụ có tất cả các cạnh bên song song và bằng nhau;
- Hình lăng trụ có 2 đáy đều là hình bình hành;
- Hình lăng trụ có tất cả các mặt bên đều là những hình chữ nhật.
| $4$ | |
| $5$ | |
| $3$ | |
| $2$ |
