Hàm số $y=\dfrac{1}{3}x^3+3x^2-7x-\dfrac{20}{3}$ nghịch biến trên khoảng nào trong những khoảng sau đây?
| $(-7;1)$ | |
| $(-7;2)$ | |
| $(-\infty;-7)$ | |
| $(1;+\infty)$ |
Cho $x,\,y$ là hai số thực dương và $m,\,n$ là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
| $\dfrac{x^m}{x^n}=x^{m-n}$ | |
| $(xy)^n=x^n\cdot y^n$ | |
| $\dfrac{x^m}{y^n}=\left(\dfrac{x}{y}\right)^{m-n}$ | |
| $\big(x^n\big)^m=x^{n\cdot m}$ |
Biết phương trình $2\log_2x+3\log_x2=7$ có $2$ nghiệm thực $x_1,\,x_2$ ($x_1< x_2$). Tính giá trị của biểu thức $T=\big(x_1\big)^{x_2}$.
| $T=32$ | |
| $T=8$ | |
| $T=16$ | |
| $T=64$ |
Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?
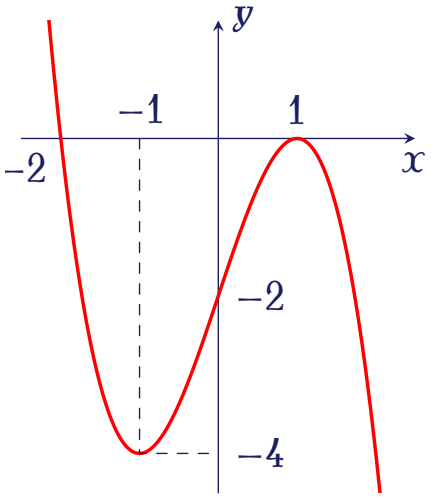
| $y=-x^3+3x-2$ | |
| $y=x^3-3x+2$ | |
| $y=x^4-3x^2-2$ | |
| $y=x^4-3x^2+2$ |
Thể tích của khối trụ có đường cao bằng $4a$, đường kính đáy bằng $a$ là
| $\dfrac{\pi a^3}{3}$ | |
| $\pi a^3$ | |
| $4\pi a^3$ | |
| $2\pi a^3$ |
Khối nón có bán kính đáy bằng $r$, chiều cao bằng $h$. Thể tích khối nón bằng
| $\pi r^2h$ | |
| $2\pi rh$ | |
| $\pi rh$ | |
| $\dfrac{1}{3}\pi r^2h$ |
Tìm nghiệm của phương trình $3^{x-1}=27$.
| $x=10$ | |
| $x=3$ | |
| $x=4$ | |
| $x=9$ |
Cắt một hình nón $(N)$ bởi một mặt phẳng đi qua trục ta được một tam giác đều có diện tích $4\sqrt{3}a^2$. Diện tích toàn phần của hình nón $(N)$ bằng
| $3\pi a^2$ | |
| $12\pi a^2$ | |
| $\pi a^2$ | |
| $6\pi a^2$ |
Cho hàm số $f(x)=\big(1-\sqrt[4]{x}\big)\big(1+\sqrt[4]{x}\big)\big(1+\sqrt{x}\big)(1+x)$. Tính $f\left(\dfrac{1}{2^{64}}\right)$.
| $1-\dfrac{1}{2^{128}}$ | |
| $1+\dfrac{1}{2^{64}}$ | |
| $1+\dfrac{1}{2^{128}}$ | |
| $1-\dfrac{1}{2^{64}}$ |
Cho hàm số $y=\dfrac{2x+1}{-x+1}$. Khẳng định nào sau đây đúng?
| Hàm số nghịch biến trên $\mathbb{R}\setminus\{1\}$ | |
| Hàm số đồng biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ | |
| Hàm số đồng biến trên $\mathbb{R}\setminus\{1\}$ | |
| Hàm số nghịch biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ |
Đồ thị hàm số nào sau đây có tiệm cận ngang?
| $y=\dfrac{1-x^2}{x}$ | |
| $y=\dfrac{\sqrt{x^2-1}}{x}$ | |
| $y=\dfrac{x^2-1}{x}$ | |
| $y=\dfrac{\sqrt{1-x^2}}{x}$ |
Bảng biến thiên trong hình bên là của hàm số nào trong các hàm số đã cho dưới đây?
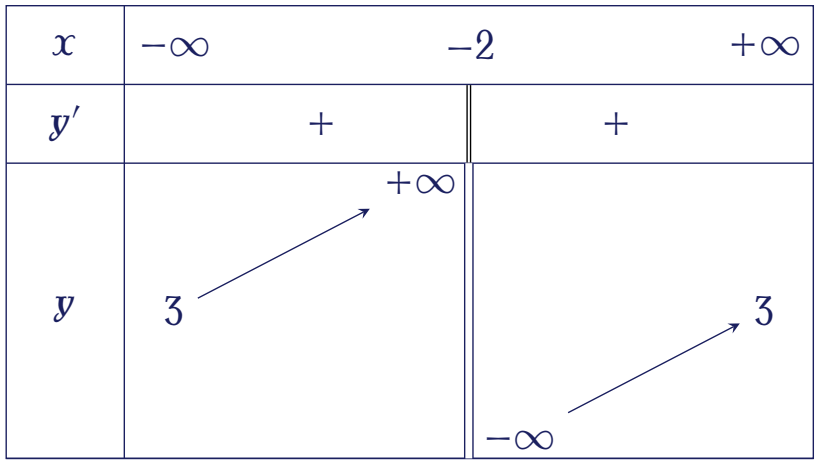
| $y=\dfrac{3-x}{x+2}$ | |
| $y=\dfrac{3x+8}{x+2}$ | |
| $y=\dfrac{3x-3}{x+2}$ | |
| $y=\dfrac{3-3x}{x+2}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$.
| $\dfrac{a^3\sqrt{3}}{18}$ | |
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{8}$ | |
| $\dfrac{a^3}{6}$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều cạnh $a$ và $AA'=2a$ (minh họa như hình vẽ bên).
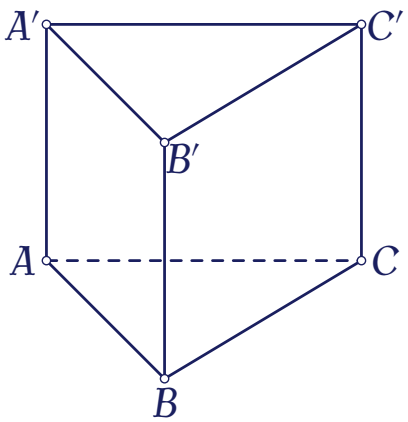
Thể tích của khối lăng trụ đã cho bằng
| $\sqrt{3}a^3$ | |
| $\dfrac{\sqrt{3}a^3}{6}$ | |
| $\dfrac{\sqrt{3}a^3}{3}$ | |
| $\dfrac{\sqrt{3}a^3}{2}$ |
Trong một khối đa diện, mệnh đề nào sau đây đúng?
| Hai cạnh bất kì có ít nhất một điểm chung | |
| Mỗi cạnh là cạnh chung của đúng $2$ mặt | |
| Mỗi đỉnh là đỉnh chung của ít nhất $2$ mặt | |
| Hai mặt bất kì có ít nhất một điểm chung |
Cho hình lập phương có tổng diện tích các mặt bằng $12a^2$. Tính theo $a$ thể tích khối lập phương đó.
| $\sqrt{2}a^3$ | |
| $a^3$ | |
| $2\sqrt{2}a^3$ | |
| $\dfrac{a^3}{3}$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x-3}$ là đường thẳng có phương trình
| $x=\dfrac{1}{2}$ | |
| $x=\dfrac{1}{3}$ | |
| $x=2$ | |
| $x=3$ |
Tích tất cả các nghiệm của phương trình $\ln\left(x-\dfrac{1}{4}\right)\cdot\ln\left(x+\dfrac{1}{2}\right)\cdot\ln(x+2)=0$ là
| $\dfrac{5}{4}$ | |
| $\dfrac{5}{8}$ | |
| $\dfrac{5}{2}$ | |
| $\dfrac{1}{4}$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Phát biểu nào sau đây đúng?
| Hàm số $y=f(x)$ đạt cực trị tại $x_0$ khi và chỉ khi $x_0$ là nghiệm của đạo hàm | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)>0$ thì hàm số đạt cực đại tại $x_0$ | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)=0$ thì $x_0$ không phải là cực trị của hàm số $y=f(x)$ đã cho | |
| Nếu $f'(x)$ đổi dấu khi $x$ qua điểm $x_0$ và $y=f(x)$ liên tục tại $x_0$ thì hàm số $y=f(x)$ đạt cực trị tại điểm $x_0$ |
